Kriteria segitiga serupa

Apa kriteria kesamaan segitiga?

Kriteria kesamaan segitiga adalah aturan yang memungkinkan untuk mengetahui apakah dua segitiga serupa. Kesamaan angka geometris, termasuk segitiga, mensyaratkan bahwa angka -angka memiliki cara yang sama, meskipun mereka tidak harus memiliki ukuran yang sama atau orientasi yang sama.

Agar dua segitiga serupa, perlu bahwa: i) sisi homolog mereka proporsional dan ii) sudut internal masing -masing memiliki ukuran yang sama.

Gambar 1. Dua segitiga serupa: meskipun mereka tidak memiliki ukuran yang sama, sisi mereka proporsional dan sudut internal mereka memiliki ukuran yang sama. Sumber: f. Zapata.

Rasio atau proporsi proporsional antara dua jumlah A dan B diwakili oleh rasio A/B, dengan B ≠ 0. Untuk segitiga yang sama, proporsi berikut di antara sisi -sisinya valid:

a/a '= b/b' = c/c '= r

Nilai R disebut alasan kesamaan.

Selain itu, sudut internal yang sesuai harus memiliki ukuran yang sama, oleh karena itu: ∠a = ∠a '; ∠B = ∠B 'dan ∠C = ∠C'. Menurut kondisi ini, kriteria kesamaan segitiga adalah:

Kriteria 1: Dua segitiga serupa jika mereka memiliki dua sudut internal dengan ukuran yang sama. Jika demikian, sudut ketiga juga mengukur hal yang sama, karena jumlah sudut internal dalam segitiga apa pun adalah 180º:

α = α '; β = β '

Kriteria 2: Segitiga serupa jika dua sisi homolog proporsional dan sudut di antara mereka sama:

a/a '= b/b'; α = α '

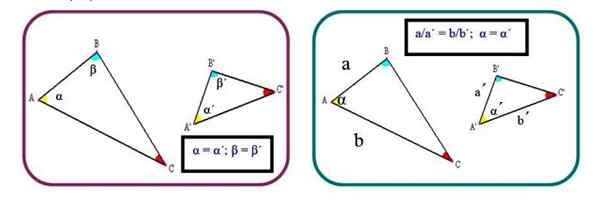Gambar 2. Dua kriteria untuk menetapkan kesamaan segitiga. Sumber: f. Zapata.

Kriteria 3: Tiga sisi homolog proporsional:

a/a '= b/b' = c/c '= r

Contoh

Kesamaan segitiga sangat berguna untuk menghitung ketinggian dan jarak yang tidak mudah diukur secara langsung. Melalui beberapa perhitungan sederhana, dimungkinkan untuk mengetahui panjang ini dengan membandingkan segitiga yang serupa.

Dapat melayani Anda: Teorema mendasar aritmatika: demonstrasi, aplikasi, latihan

Tinggi kolom, bangunan dan pohon

Dikatakan bahwa bapak geometri di Yunani kuno, seperti Miletus (625-547.C.), menghitung ketinggian kolom kuil tanpa perlu instrumen khusus, cukup membandingkan panjang bayangan tongkatnya dengan kolom dan menerapkan kesamaan segitiga. Dengan metode yang sama ia berhasil mengukur ketinggian piramida besar Mesir dan dengan demikian mengesankan firaun.

Jarak ke Bulan

Ada percobaan sederhana yang dilakukan untuk menghitung jarak antara bumi dan bulan. Itu membutuhkan mata uang, sedikit pita perekat dan aturan vernier atau pascasarjana. Saat bulan penuh, mata uang melekat pada gelas jendela dan bulan diamati dengan satu mata, terletak sedemikian rupa sehingga mata uang hanya menutupi bulan purnama.

Ketika ini terjadi, alasan antara diameter mata uang dan jarak antara mata dan mata uang, adalah sama bahwa ada antara diameter bulan dan jarak antara mata dan bulan:

Diameter Mata Uang/Jarak Mata Uang = Diameter Bulan/Jarak ke Bulan

Alasannya sekitar 1/110. Yang berarti bahwa jarak ke bulan adalah 110 kali diameter dari ini.

Saat ini jari -jari bulan diperkirakan pada 1737.1 km, jadi diameternya 3474.2 km. Dengan mengganti nilai ini dalam hubungan:

Jarak ke bulan = Diameter bulan ÷ (diameter mata uang/jarak ke mata uang)

Diperoleh:

Jarak ke bulan = 3474.2 km ÷ (1/110) = 382.162 km

Itu bisa melayani Anda: prisma hepagonal

Sangat dekat dengan nilai yang ditetapkan oleh 384 astronom.000 km.

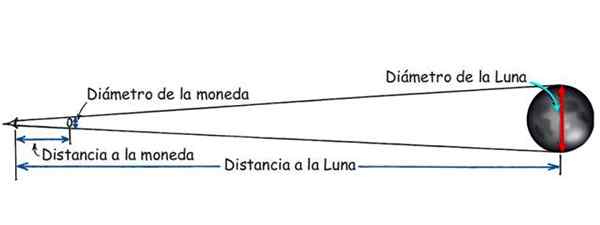Gambar 3. Jarak ke bulan dapat diketahui berkat kesamaan segitiga. Sumber: Hewitt yang dimodifikasi, p. Fisika Konseptual.

Jarak antara kapal dan pantai

Untuk mengukur jarak antara kapal dan pantai, taruhannya terjebak di pantai di titik A, B, C dan Q. Segitiga ABC dan PCQ serupa dengan kriteria 1, karena mereka memiliki dua sudut yang sama: dua sudut ∠c = α yang ditentang oleh simpul dan dua sudut lurus sama dengan 90º: ∠B = ∠Q.

Dua segitiga yang terletak dengan cara ini dikatakan masuk Posisi Thales Dan mereka selalu serupa. Segitiga diidentifikasi dalam posisi thales untuk memiliki sudut yang sama dan sisi yang berlawanan pada sudut itu paralel.

Di bagian selanjutnya ada latihan dengan nilai numerik.

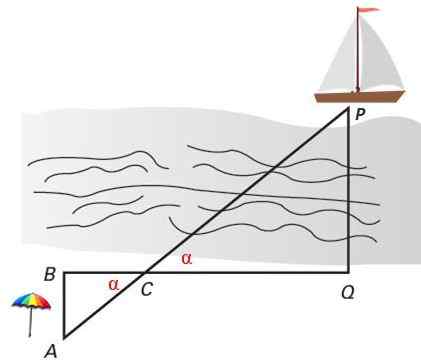Gambar 4. Dua segitiga serupa di posisi Thales berfungsi untuk menghitung jarak tegak lurus kapal ke pantai. Sumber: f. Zapata.

Latihan terpecahkan

Latihan 1

Anda ingin mengetahui seberapa jauh perahu layar berlabuh pada gambar sebelumnya, dari titik yang terletak di pantai pantai, yang taruhannya dipaku di titik A, B, C dan Q, sehingga menentukan segitiga ABC, yang mana mirip dengan PCQ, tetapi sisi yang lebih mudah diukur.

Hitung PQ jarak tegak lurus antara kapal dan pantai, dengan kesamaan segitiga, jika jarak yang tersedia adalah:

AB = 12 m

Bc = 16 m

QC = 60 m

Larutan

Proporsi antara sisi homolog adalah:

Ab/qp = bc/cq = 16 m/60 m = 0.267

Oleh karena itu 0.267 adalah alasan kesamaan:

AB/QP = 0.267

QP = AB / 0.267 = 12 m / 0.267 = 44.9 m

Latihan 2

Dalam segitiga berikut: berapa ukuran segmen AD?

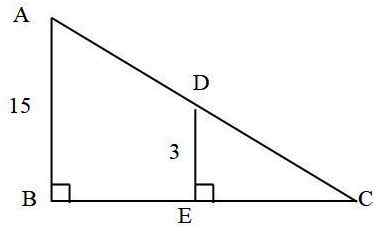
Diketahui bahwa:

• Ac = 25 cm
• AB = 15 cm
• De = 3 cm

Dapat melayani Anda: kelipatan 2: apa itu dan penjelasan

Larutan

Segitiga itu serupa, karena mereka berbagi sudut yang ∠c dan sisi dan ab paralel. Rasio kesamaan dihitung oleh:

R = ab / de = 15 cm / 3 cm = 5

Dan juga melalui:

R = AC / DC

Oleh karena itu dc = ac / r = 25 cm / 5 = 5 cm

Sejak:

Ac = iklan + dc

Ini mengikuti iklan = ac - dc = 25 cm - 5 cm = 20 cm

Latihan 3

Segitiga Isosceles memiliki perimeter 49 cm dan dasar 21 cm. Hitung perimeter segitiga yang mirip dengan ini, tetapi yang basisnya berukuran 4 cm.

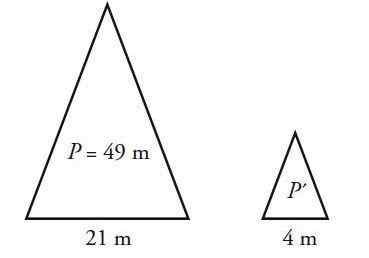
Larutan

Segitiga Isosceles memiliki dua sisi yang sama, berbeda dari pangkalan B. Biarkan ℓ ukuran sisi dan p perimeter, yang terdiri dari jumlah ketiga sisi. Untuk segitiga terbesar:

P = 2 ℓ + b = 49 cm

2 ℓ + 21 cm = 49 cm → ℓ = (49-21) cm / 2 = 14 cm

Sekarang proporsi antara sisi segitiga dinaikkan, yang dari segitiga kecil dilambangkan dengan premi:

B/ b '= ℓ/ ℓ'

21 cm / 4cm = 14 cm / ℓ '→ ℓ' = 14 cm / (21 cm / 4cm) = 2.67 cm

Perimeter segitiga kecil adalah:

P '= 2 ℓ' + b '= (2 x 2.67) cm + 4 cm = 9.33 cm.

Referensi

1. Alexander, d. 2013. Geometri. Ke -5. Edisi. Pembelajaran Cengage.
2. Hewitt, Paul. 2012. Ilmu Fisik Konseptual. Ke -5. Ed. Pearson.
3. Clemens, s. Geometri dengan aplikasi. Addison Wesley.
4. Ibáñez, hlm. 2010. Matematika III. Pembelajaran Cengage.
5. Jiménez, r. Matematika II: Geometri dan Trigonometri. 2nd. Edisi. Pearson.
6. Stewart, J. 2007. Prekalkulasi. Ke -5. Edisi. Pembelajaran Cengage.
7. Vicmat. Samos Aristarco: Ukuran Tata Surya. Pulih dari: vicmat.com