Definisi Curtosis, Jenis, Rumus, untuk apa, misalnya

Itu Curtosis atau kurtosis Ini adalah parameter statistik yang berfungsi untuk mengkarakterisasi distribusi probabilitas variabel acak, menunjukkan tingkat konsentrasi nilai di sekitar ukuran pusat. Ini juga dikenal sebagai "kelas puncak".

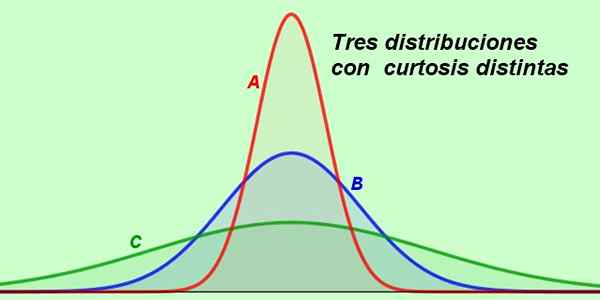
Istilah ini berasal dari "kurtos" Yunani yang berarti melengkung, oleh karena itu curtosis menunjukkan tingkat menunjuk atau meratakan distribusi, seperti yang terlihat pada gambar berikut:

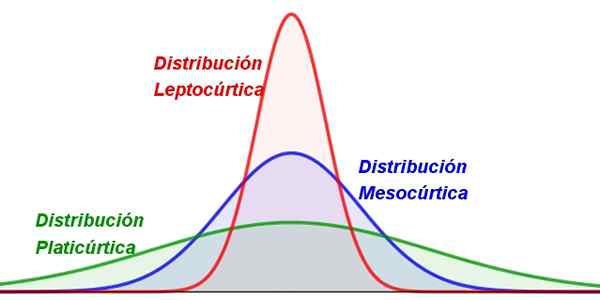Gambar 1. Berbagai jenis Curtosis. Sumber: f. Zapata.

Hampir semua nilai variabel acak cenderung mengelompok di sekitar nilai sentral seperti rata -rata. Tetapi dalam beberapa distribusi, nilainya lebih tersebar daripada yang lain, menghasilkan kurva yang lebih rata atau lebih ramping.

[TOC]

Definisi

Curtosis adalah nilai numerik dari setiap distribusi frekuensi, yang menurut konsentrasi nilai di sekitar rata -rata, diklasifikasikan ke dalam tiga kelompok:

-Leptocuric: di mana nilainya sangat dikelompokkan di sekitar rata -rata, sehingga distribusinya cukup runcing dan ramping, (Gambar 1, kiri).

-Mesocuric: Ini memiliki konsentrasi nilai yang sedang sekitar rata -rata (Gambar 1 di tengah).

-Phylicuric: Distribusi ini memiliki bentuk yang lebih luas, karena nilai -nilai cenderung lebih tersebar (Gambar 1 di sebelah kanan).

Rumus dan Persamaan

Curtosis dapat memiliki nilai apa pun, tanpa batasan. Perhitungannya dilakukan tergantung pada cara data dikirimkan. Notasi yang digunakan dalam setiap kasus adalah sebagai berikut:

-Koefisien Kortosis: G₂

-Rata -rata aritmatika: X atau x dengan bar

-I-EME: X_yo

-Deviasi standar: σ

-Jumlah data: N

-Frekuensi I-ESIMO: F_yo

-Merek kelas: MX_yo

Dengan notasi ini, kami menyajikan beberapa formula yang paling umum digunakan untuk menemukan Curtosis:

Dapat melayani Anda: ruang vektor: basis dan dimensi, aksioma, properti

- Curtosis sesuai dengan penyajian data

Tanpa pengelompokan atau dikelompokkan data pada frekuensi

Data dikelompokkan secara berkala

Kelebihan Curtosis

Disebut juga Koefisien penunjuk Fisher salah satu Ukuran Fisher, Itu berfungsi untuk membandingkan distribusi yang diteliti dengan distribusi normal.

Ketika Curtosis Kelebihan Layak 0, kita berada di hadapan Distribusi Normal atau Gauss Bell. Dengan cara ini, selama penyamaan berlebih dari distribusi dihitung, kami sebenarnya membandingkannya dengan distribusi normal.

Baik untuk data tanpa pengelompokan dan untuk data yang dikelompokkan, koefisien penunjuk Fisher, dilambangkan dengan K, adalah: adalah:

K = G₂ - 3

Namun, dapat ditunjukkan bahwa curtosis distribusi normal adalah 3, oleh karena itu jika koefisien penunjuk fisher adalah 0 atau mendekati 0 dan ada distribusi mesokurik. Jika k> 0 distribusinya adalah leptocuric dan jika k<0 es platicúrtica.

Untuk apa Curtosis?

Curtosis adalah ukuran variabilitas yang digunakan untuk mengkarakterisasi morfologi distribusi. Dengan cara ini, distribusi simetris dapat dibandingkan dengan rata -rata yang sama dan dispersi yang sama (diberikan oleh standar deviasi).

Memiliki ukuran variabilitas memastikan bahwa rata -rata dapat diandalkan dan membantu mengontrol variasi distribusi. Sebagai contoh, mari kita analisis dua situasi ini.

3 gaji departemen

Misalkan grafik berikut menunjukkan distribusi dalam gaji 3 departemen dari perusahaan yang sama:

Gambar 2. Tiga distribusi yang berbeda menggambarkan situasi praktis. (Disiapkan oleh fanny zapata)

Kurva A adalah yang paling ramping dari semuanya, dan dalam bentuknya disimpulkan bahwa sebagian besar gaji departemen itu sangat dekat dengan rata -rata, oleh karena itu sebagian besar karyawan menerima kompensasi yang sama.

Dapat melayani Anda: bilangan bulat

Untuk bagiannya di Departemen B, kurva gaji mengikuti distribusi normal, karena kurva adalah mesokur, di mana kami mengasumsikan bahwa gaji didistribusikan secara acak.

Dan akhirnya kita memiliki kurva C yang sangat rata, tanda bahwa di departemen ini kisaran gaji jauh lebih luas daripada yang lain.

Hasil ujian

Misalkan sekarang bahwa tiga kurva dari Gambar 2 mewakili hasil ujian yang diterapkan pada tiga kelompok siswa dari subjek yang sama.

Kelompok yang kualifikasinya diwakili oleh kurva ke leptocuric, cukup homogen, paling memperoleh peringkat rata -rata atau dekat.

Mungkin juga hasilnya disebabkan oleh fakta bahwa pertanyaan ujian memiliki tingkat kesulitan yang kurang lebih sama.

Di sisi lain, hasil kelompok C menunjukkan heterogenitas yang lebih besar dalam kelompok, yang mungkin berisi rata -rata siswa, beberapa siswa yang lebih berprestasi dan tentunya tidak terlalu perhatian lainnya.

Atau itu bisa berarti bahwa pertanyaan tes memiliki tingkat kesulitan yang sangat berbeda.

Kurva B adalah mesokur, menunjukkan bahwa hasil tes mengikuti distribusi normal. Ini biasanya kasus yang paling sering.

Contoh Curtosis Terpecahkan

Temukan koefisien penunjuk Fisher untuk nilai -nilai berikut, diperoleh dalam ujian fisika untuk sekelompok siswa, dengan skala dari 1 hingga 10:

5, 5, 4, 7, 7.7, 9, 8, 9, 4, 3

Larutan

Ekspresi berikut akan digunakan untuk data yang tidak dikelompokkan, diberikan pada bagian sebelumnya:

Dengan koefisien titik Fisher yang diberikan oleh:

Dapat melayani Anda: identitas Pythagoras: demonstrasi, contoh, latihan

K = g₂ - 3

Nilai ini memungkinkan untuk mengetahui jenis distribusi.

Untuk menghitung g₂ Lebih mudah untuk melakukannya dengan cara yang tertib, langkah demi langkah, karena beberapa operasi aritmatika harus diselesaikan.

Langkah 1

Pertama, rata -rata kualifikasi dihitung. Ada n = 11 data.

X = (5+5+4+7+7+7+9+8+9+4+3)/11 = 6.182

Langkah 2

Deviasi standar ditemukan, di mana persamaan ini digunakan:

 Dengan menggunakan kalkulator dengan fungsi statistik hasilnya langsung:

σ = 1.992

Atau Anda juga dapat membuat tabel, yang juga diperlukan untuk langkah berikutnya dan di mana setiap istilah ringkasan yang akan diperlukan ditulis, dimulai dengan (x_yo - X), lalu (x_yo - X)² Dan kemudian (x_yo - X)⁴ :

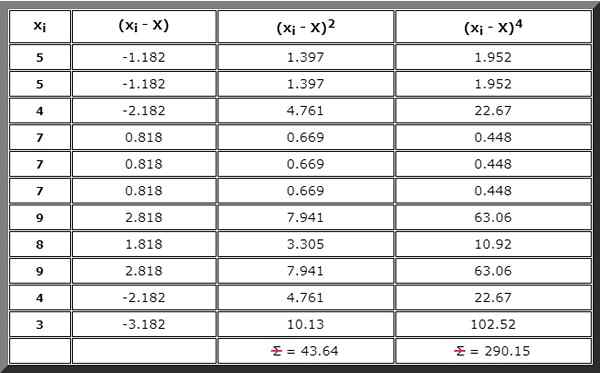
Langkah 3

Melakukan jumlah yang ditunjukkan dalam pembilang formula untuk g₂. Untuk ini, hasil kolom kanan tabel sebelumnya digunakan:

∑ (X_yo - X)⁴= 290.limabelas

Karena itu:

G₂ = (1/11) x 290.15/1.992⁴ = 1.675

Koefisien papan nama Fisher adalah:

K = g₂ - 3 = 1.675 - 3 = -1.325

Minat apa yang merupakan tanda hasil, yang, ketika negatif, sesuai dengan sekejap tingkat kesulitan yang berbeda.

Penggunaan spreadsheet seperti Excel, sangat memfasilitasi resolusi dari jenis masalah ini dan juga menawarkan opsi untuk membuat grafik distribusi.

Referensi

1. Levin, r. 1988. Statistik untuk administrator. 2nd. Edisi. Prentice Hall.
2. Marco, f. Curtosis. Pulih dari: economipedia.com.
3. Oliva, J. Asimetri dan Curtosis. Diperoleh dari: StatisticsAucv.File.WordPress.com.
4. Spurr, w. 1982. Pengambilan keputusan dalam administrasi. Limusa.
5. Wikipedia. Kurtosis. Diperoleh dari: di.Wikipedia.org.