Probabilitas Jenis Aksioma, Penjelasan, Contoh, Latihan

Itu aksioma kemungkinan Mereka adalah proposisi matematika mengenai teori probabilitas, yang tidak pantas demonstrasi. Aksioma didirikan pada tahun 1933 oleh ahli matematika Rusia Andrei Kolmogorov (1903-1987) dalam karyanya Dasar -dasar Teori Probabilitas dan meletakkan dasar dari studi matematika probabilitas.

Saat melakukan percobaan acak tertentu ξ, ruang sampel adalah yang bersama dengan semua hasil yang mungkin dari percobaan, juga disebut Acara. Peristiwa apa pun dilambangkan sebagai A dan P (A) adalah probabilitas terjadi. Kemudian Kolmogorov menetapkan itu:

Gambar 1. Probabilitas Aksioma memungkinkan untuk menghitung probabilitas memukul perjudian seperti roulette. Sumber: Pixabay.

-Aksioma 1 (tidak ada negatif): Probabilitas bahwa setiap peristiwa terjadi selalu positif atau nol, P (a) ≥0. Ketika probabilitas suatu peristiwa adalah 0, itu disebut Peristiwa yang tidak mungkin.

-Aksioma 2 (kepastian): asalkan beberapa peristiwa milik E, probabilitas kejadiannya adalah 1, yang dapat kita ungkapkan sebagai P (e) = 1. Adalah apa yang dikenal sebagai a Acara yang aman, Karena saat melakukan percobaan, ada hasil dengan semua kepastian.

-Axioma 3 (penambahan): Dalam kasus dua atau lebih peristiwa yang tidak kompatibel dua banding dua, dipanggil₁, KE₂, KE₃..., probabilitas acara₁ lebih a₂ lebih a₃ Dan seterusnya, itu adalah jumlah probabilitas yang masing -masing terjadi secara terpisah.

Ini dinyatakan sebagai: P (a₁ U a₂ U a₃ U ...) = p (a₁) + P (a₂) + P (a₃) +..

Gambar 2. Matematikawan Rusia yang luar biasa Andrei Kolmogorov (1903-1987), yang meletakkan fondasi untuk probabilitas aksiomatik. Sumber: Wikimedia Commons.

[TOC]

Contoh

Aksioma probabilitas banyak digunakan dalam banyak aplikasi. Misalnya:

Cakar atau Tachuela dilemparkan ke udara, dan ketika lantai jatuh, ada pilihan untuk jatuh dengan ujung ke atas (u) atau dengan ujung ke bawah (D) (kami tidak akan mempertimbangkan kemungkinan lain). Ruang sampel percobaan ini terdiri dari peristiwa ini, lalu e = u, d.

Dapat melayani Anda: Revolusi Padatan: Volume, Jenis, Latihan TerpecahkanGambar 3. Dalam percobaan meluncurkan Tachuela ada dua peristiwa dengan probabilitas yang berbeda: jatuh dengan ujung ke atas atau ke lantai. Sumber: Pixabay.

Dengan menerapkan aksioma yang kita miliki:

P (e) = 1 (Axioma 2)

Tetapi P (e) = p (u) + p (d) (Axioma 3), karena peristiwa ini tidak kompatibel, atau terputus -putus. Bug tidak jatuh dengan ujung ke atas atau ke bawah pada saat yang sama, itu adalah satu atau yang lain, tetapi tidak keduanya, karena kemungkinan lain sedang dipertimbangkan. Jadi:

P (u) + p (d) = 1

P (u) = 1 - p (d)

Jika sama -sama cenderung jatuh dengan ujung ke atas atau ke bawah, P (u) = p (d) = ½ (Axioma 1). Namun, mungkin karena konstruksi dan desain bug. Misalnya, mungkin itu P (u) = ¾ ketika P (d) = ¼ (Axioma 1).

Perhatikan bahwa dalam kedua kasus, jumlah probabilitas memberikan 1. Namun, aksioma tidak menunjukkan bagaimana mengalokasikan probabilitas, setidaknya tidak sepenuhnya. Tetapi mereka menegaskan bahwa mereka adalah angka antara 0 dan 1 dan bahwa, seperti yang terjadi dalam kasus ini, jumlah semuanya adalah 1.

Cara untuk menetapkan probabilitas

Aksioma probabilitas bukan merupakan metode penetapan nilai probabilitas. Untuk ini ada tiga opsi yang kompatibel dengan aksioma:

Aturan Laplace

Setiap peristiwa diberikan probabilitas yang sama untuk terjadi, maka probabilitas kejadian didefinisikan sebagai:

P (a) = jumlah kasus yang menguntungkan untuk acara a/ jumlah kasus yang mungkin terjadi

Misalnya, berapa probabilitas mengekstraksi kartu as dari setumpuk kartu Prancis? Dek memiliki 52 kartu, 13 dari masing -masing tongkat dan ada 4 tongkat. Setiap tongkat memiliki 1 AS, jadi total ada 4 ace:

P (as) = ​​4/52 = 1/13

Aturan Laplace terbatas pada ruang sampel yang terbatas, di mana setiap peristiwa sama -sama mungkin.

Dapat melayani Anda: matematika diskrit

Frekuensi relatif

Di sini percobaan harus diulang, karena metode ini didasarkan pada melakukan sejumlah besar pengulangan.

Mari kita lakukan pengulangan percobaan ξ, yang kami temukan bahwa n adalah berapa kali yang terjadi pada peristiwa tertentu, maka probabilitas bahwa peristiwa ini akan terjadi adalah:

P (a) = lim_{I → ∞} (juga tidak)

Di mana n/i adalah frekuensi relatif dari suatu peristiwa.

Tentukan p (a) dengan cara ini memuaskan aksioma Kolmogorov, tetapi memiliki ketidaknyamanan bahwa banyak tes harus dilakukan sehingga probabilitasnya tepat.

Metode subyektif

Seseorang atau sekelompok orang dapat setuju untuk memberikan probabilitas untuk suatu peristiwa, melalui penilaian mereka sendiri. Metode ini memiliki kelemahan yang dapat ditetapkan oleh orang yang berbeda.

Olahraga diselesaikan

Dalam percobaan secara bersamaan meluncurkan 3 mata uang jujur, memperoleh peluang peristiwa yang dijelaskan:

a) 2 wajah dan salib.

b) 1 wajah dan dua salib

c) 3 salib.

D) setidaknya 1 wajah.

Solusi untuk

Wajah dilambangkan dengan C dan salib dengan x. Tetapi ada beberapa cara untuk mendapatkan dua wajah dan salib. Misalnya, dua koin pertama bisa jatuh dengan wajah dan yang ketiga dengan Cruz. Atau yang pertama bisa jatuh wajah, salib kedua dan wajah ketiga. Dan akhirnya yang pertama bisa menjadi salib dan wajah yang tersisa.

Untuk menjawab pertanyaan, perlu mengetahui semua kemungkinan, yang dijelaskan dalam alat yang disebut diagram pohon salah satu Pohon probabilitas:

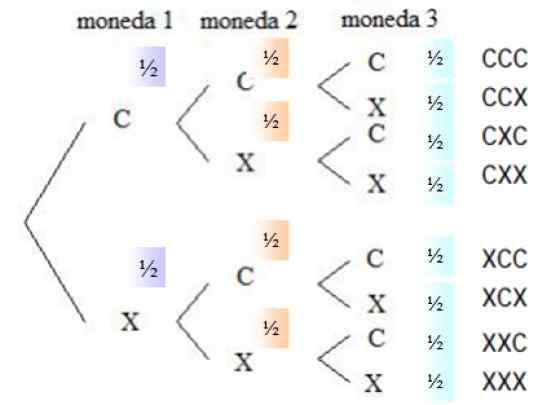Gambar 4. Diagram pohon untuk peluncuran tiga koin jujur ​​secara bersamaan. Sumber: f. Zapata.

Probabilitas bahwa dalam mata uang apa pun mahal adalah ½, hal yang sama terjadi untuk salib, karena mata uangnya jujur. Di kolom kanan, semua kemungkinan peluncuran terdaftar, yaitu ruang sampel.

Dapat melayani Anda: variabel statistik

Kombinasi yang menanggapi acara yang diminta dipilih dari ruang sampel, karena urutan di mana wajah muncul tidak penting. Ada tiga acara yang menguntungkan: CCX, CXC dan XCC. Probabilitas setiap peristiwa adalah:

P (ccx) = ½. ½ . ½ = 1/8

Hal yang sama terjadi untuk acara CXC dan XCC, masing -masing memiliki 1/8 probabilitas untuk terjadi. Oleh karena itu probabilitas mendapatkan tepat 2 wajah adalah jumlah probabilitas semua peristiwa yang menguntungkan:

P (2 wajah) = 1/8 + 1/8 + 1/8 = 3/8 = 0.375

Solusi b

Menemukan probabilitas bahwa ada dua persilangan adalah masalah analog dengan yang sebelumnya, ada juga tiga peristiwa yang menguntungkan yang diambil dari ruang sampel: CXX, XCX dan XXC. Karena itu:

P (2 silang) = 3/8 = 0.375

Solusi c

Secara intuitif ketahui bahwa probabilitas mendapatkan 3 salib (atau 3 wajah) lebih rendah. Dalam hal ini, peristiwa yang dicari adalah xxx, di akhir kolom kanan, yang probabilitasnya adalah:

P (xxx) = ½. ½. ½ = 1/8 = 0.125.

Solusi d

Itu diminta untuk mendapatkan setidaknya 1 wajah, ini berarti bahwa 3 wajah, 2 wajah atau 1 wajah bisa pergi. Satu -satunya peristiwa yang tidak kompatibel dengan ini adalah satu di mana 3 salib keluar, yang probabilitasnya adalah 0.125. Oleh karena itu probabilitas yang dicari adalah:

P (setidaknya 1 wajah) = 1 - 0.125 = 0.875.

Referensi

1. Canavos, g. 1988. Probabilitas dan Statistik: Aplikasi dan Metode. Bukit McGraw.
2. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
3. Lipschutz, s. 1991. Seri Schaum: Probabilitas. Bukit McGraw.
4. Obregón, i. 1989.Teori probabilitas. Limusa editorial.
5. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.