Derivatif Aljabar

Apa itu turunan aljabar?

Itu Derivatif Aljabar Mereka terdiri dari studi turunan dalam kasus tertentu dari fungsi aljabar. Asal usul gagasan turunannya berasal dari Yunani kuno. Pengembangan gagasan ini dimotivasi oleh kebutuhan untuk menyelesaikan dua masalah penting, satu dalam fisika dan satu dalam matematika.

Dalam fisika, turunannya memecahkan masalah menentukan kecepatan instan dari objek yang bergerak. Dalam matematika, ini memungkinkan untuk menemukan garis garis singgung ke kurva pada titik tertentu.

Meskipun sebenarnya ada lebih banyak masalah yang diselesaikan dengan menggunakan turunan, serta generalisasi, hasil yang kemudian datang ke pengenalan konsep mereka.

Pelopor kalkulus diferensial adalah Newton dan Leibniz. Sebelum memberikan definisi formal, kami akan mengembangkan ide di belakang, dari sudut pandang matematika dan fisik.

Turunan sebagai menunggu garis garis singgung ke kurva

Misalkan grafik fungsi y = f (x) adalah grafik kontinu (tanpa paku atau simpul atau pemisahan), dan baik a = (a, f (a)) titik tetap di atasnya. Kami ingin menemukan persamaan garis garis singgung dengan fungsi f pada titik a.

Mari kita ambil titik lain p = (x, f (x)) dari grafik, dekat dengan titik A, dan melacak garis pengeringan yang melewati A dan P. Garis pengeringan adalah garis yang memotong grafik kurva menjadi satu atau lebih titik.

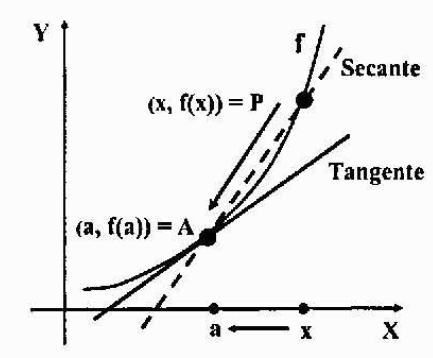
Untuk mendapatkan garis garis singgung yang kita inginkan, hanya perlu menghitung kemiringan karena kita sudah memiliki titik garis: titik a.

Jika kami memindahkan titik P oleh grafik dan kami mendekatinya lebih dan lebih ke titik A, garis kering yang disebutkan sebelumnya akan mendekati garis garis singgung yang ingin Anda temukan. Mengambil batas ketika "p cenderung ke", kedua baris akan bertepatan, oleh karena itu lereng mereka juga.

Kemiringan garis sekte diberikan oleh

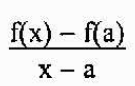
Mengatakan bahwa p dekat dengan a, setara dengan mengatakan bahwa "x" mendekati "a". Dengan demikian, kemiringan garis garis singgung ke grafik F pada titik A akan sama dengan:

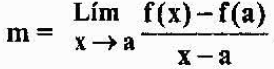
Ekspresi sebelumnya dilambangkan dengan f '(a), dan didefinisikan sebagai turunan dari fungsi f pada titik "a". Kami melihat bahwa secara analitis, turunan dari suatu fungsi pada suatu titik adalah batas, tetapi secara geometris, itu adalah kemiringan garis garis singgung ke bagan fungsi pada titik tersebut.

Dapat melayani Anda: variabel acak: konsep, jenis, contoh

Sekarang kita akan melihat gagasan ini dari sudut pandang fisika. Kami akan mencapai ekspresi yang sama dari batas sebelumnya, meskipun dengan jalur yang berbeda, sehingga mendapatkan suara bulat dari definisi tersebut.

Turunan sebagai kecepatan instan dari objek bergerak

Mari kita lihat contoh singkat tentang apa arti kecepatan seketika. Ketika dikatakan, misalnya, bahwa mobil untuk mencapai tujuan melakukannya dengan kecepatan 100 km per jam, artinya dalam satu jam ia menempuh jarak 100 km.

Ini tidak selalu berarti bahwa selama jam seluruh mobil selalu 100 km, vecimeter mobil dapat menandai lebih sedikit atau lebih. Jika dia memiliki kebutuhan untuk berdiri di lampu lalu lintas, kecepatan pada saat itu adalah 0 km. Namun, setelah satu jam, rute itu 100 km.

Inilah yang dikenal sebagai kecepatan rata -rata dan diberikan oleh hasil bagi jarak yang ditempuh antara waktu yang berlalu, seperti yang baru saja kita lihat. Kecepatan sesaat, sementara itu, adalah yang menandai jarum velocimeter mobil pada saat tertentu (waktu).

Mari kita lihat ini sekarang lebih umum. Misalkan suatu objek bergerak di sepanjang garis dan bahwa perpindahan ini diwakili dengan menggunakan persamaan s = f (t), di mana variabel t mengukur waktu dan variabel s pemindahan, dengan mempertimbangkan awalnya pada saat t = 0, pada saat itu juga nol, yaitu, f (0) = 0.

Fungsi ini f (t) dikenal sebagai fungsi posisi.

Ekspresi untuk kecepatan instan objek dicari pada saat yang tetap. Pada kecepatan ini kita akan menunjukkannya dengan V (a).

Baik itu setiap saat dekat dengan instan "a". Dalam interval waktu antara "a" dan "t", perubahan posisi diberikan oleh f (t) -f (a).

Kecepatan rata -rata dalam interval waktu ini adalah:

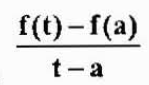
Yang merupakan perkiraan kecepatan instan v (a). Pendekatan ini akan lebih baik karena T semakin dekat dengan "A". Karena itu,

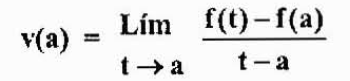
Mari kita perhatikan bahwa ungkapan ini sama dengan yang diperoleh dalam kasus sebelumnya, tetapi dari perspektif yang berbeda. Inilah yang dikenal sebagai turunan dari fungsi F pada titik "a" dan dilambangkan dengan f '(a), seperti yang dinyatakan di atas.

Dapat melayani Anda: hukum eksponen

Perhatikan bahwa membuat perubahan h

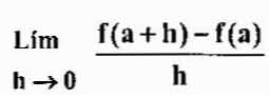
Kedua ekspresi itu setara tetapi kadang -kadang harus digunakan lebih banyak untuk satu daripada yang lain, tergantung pada kasusnya.

Kemudian didefinisikan secara lebih umum yang berasal dari fungsi f pada titik mana pun "x" milik domainnya sebagai

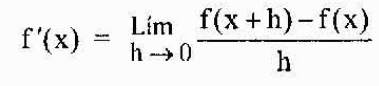
Notasi yang paling umum untuk mewakili turunan dari suatu fungsi y = f (x) adalah yang baru saja kita lihat (f 'o y'). Namun, notasi lain yang banyak digunakan adalah notasi Leibniz yang direpresentasikan sebagai salah satu dari ekspresi berikut:

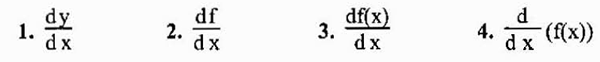
Mengingat fakta bahwa turunan pada dasarnya adalah batas, mungkin atau mungkin tidak ada, karena batasnya tidak selalu ada. Jika ada, dikatakan bahwa fungsi yang dimaksud dapat dibedakan pada titik yang diberikan.

Fungsi aljabar

Fungsi aljabar adalah kombinasi polinomial melalui jumlah, pengurangan, produk, quotient, kekuatan dan radikal.

Polinomial adalah ekspresi bentuk

P_N= a_NX^N+ ke_N-1X^N-1+ ke_N-2X^N-2+... + a₂X²+ ke₁x+a₀

Di mana n adalah angka alami dan semua_yo, Dengan i = 0,1, ..., n adalah bilangan rasional dan_N≠ 0. Dalam hal ini dikatakan bahwa tingkat polinomial ini adalah n.

Berikut ini adalah contoh fungsi aljabar:

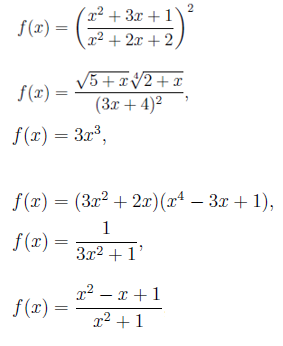
Di sini fungsi eksponensial, logaritmik dan trigonometri tidak termasuk. Aturan derivasi yang akan kita lihat di bawah ini berlaku untuk fungsi secara umum, tetapi kami akan membatasi dan menerapkannya dalam hal fungsi aljabar.

Aturan Derrying

Berasal dari konstan

Menyatakan bahwa turunan dari konstanta adalah nol. Yaitu, jika f (x) = c, maka f '(x) = 0. Misalnya, turunan fungsi konstan 2 sama dengan 0.

Berasal dari kekuatan

Jika f (x) = x^N, lalu f '(x) = nx^N-1. Misalnya, turunan x³ Itu 3x². Sebagai konsekuensi dari ini, diperoleh bahwa yang berasal dari fungsi identitas f (x) = x adalah f '(x) = 1x^1-1= x⁰= 1.

Contoh lain adalah sebagai berikut: Misalkan f (x) = 1/x², lalu f (x) = x^-2 dan f '(x) = -2x^-2-1= -2x^-3.

Properti ini juga merupakan akar yang valid, karena akarnya adalah kekuatan rasional dan di atas juga dapat diterapkan dalam kasus itu. Misalnya, yang berasal dari akar kuadrat diberikan oleh

Itu dapat melayani Anda: estimasi berdasarkan interval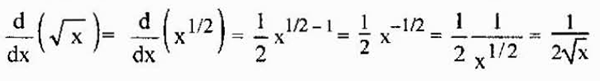

Berasal dari jumlah dan pengurangan

Jika f dan g adalah fungsi yang dapat dibedakan dalam x, maka jumlah f+g juga dan dipenuhi bahwa (f+g) '(x) = f' (x)+g '(x) (x) (x).

Demikian pula Anda harus (f -g) '(x) = f' (x) -g '(x). Dengan kata lain, turunan dari jumlah (pengurangan) adalah jumlah (atau pengurangan) dari turunannya.

Contoh

Jika h (x) = x²+X-1, kalau begitu

H '(x) = (x²)+(x) '-(1)' = 2x+1-0 = 2x+1.

Produk yang berasal dari suatu produk

Jika F dan G adalah fungsi yang dapat dibedakan dalam x, maka produk FG juga dapat dibedakan dalam x dan dipenuhi itu

(fg) '(x) = f' (x) g (x)+f (x) g '(x).

Sebagai akibatnya, ia memiliki jika C adalah konstanta dan F adalah fungsi yang dapat dibedakan dalam x, maka CF juga dapat dibedakan dalam x y (cf) '(x) = cf' (x).

Contoh

Jika f (x) = 3x (x²+1), lalu

f '(x) = (3x)' (x²+1)+(3x) (x²+1) '= 3 (x)' (x²+1)+3x [(x²) '+(1)]

= 3 (1) (x²+1)+3x [(2x^2-1) +0] = 3 (x²+1)+3x (2x) = 3x²+3+6x²

= 9x²+3.

Berasal dari hasil bagi

Jika f dan g dapat dibedakan dalam x dan g (x) ≠ 0, maka f/g juga dapat dibedakan dalam x, dan dipenuhi itu

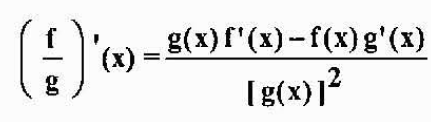
Contoh: Jika h (x) = x³/(X²-5x), lalu

H '(x) = [(x³) '(X⁵-5x)-(x³) (X⁵-5x) ']/ (x⁵-5x)²= [(3x²) (X⁵-5x)- (x³) (5x⁴-5)]/ (x⁵-5x)².

Aturan rantai

Aturan ini memungkinkan untuk memperoleh komposisi fungsi. Ini menetapkan yang berikut: Jika y = f (u) dapat dibedakan pada u, dan u = g (x) dapat dibedakan dalam x, maka fungsi senyawa f (g (x)) dapat dibedakan dalam x, dan dipenuhi itu [F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F G (x))]]]] '= f' (g (x)) g '(x).

Yaitu, turunan dari fungsi senyawa adalah produk turunan dari fungsi eksternal (turunan eksternal) oleh fungsi internal yang diturunkan (turunan internal).

Contoh

Jika f (x) = (x⁴-2x)³, Jadi

f '(x) = 3 (x⁴-2x)²(X⁴-2x) '= 3 (x⁴-2x)²(4x³-2).

Ada juga hasil untuk menghitung turunan konverse dari suatu fungsi, serta generalisasi untuk turunan orde tinggi. Aplikasi luas. Di antara mereka, keuntungan mereka dalam optimasi dan fungsi minimum disorot.

Referensi

1. Alarcon, s., González, m., & Quintana, h. (2008). Kalkulus diferensial. Itu.
2. Cabrera, v. M. (1997). 4000 perhitungan. Progreso editorial.
3. Castaño, h. F. (2005). Matematika sebelum perhitungan. Universitas Medellin.
4. Eduardo, n. KE. (2003). Pengantar Perhitungan. Edisi Umbral.
5. Sumber, a. (2016). Matematika Dasar. Pengantar Perhitungan. Lulu.com.
6. Purcell, e. J., Rigdon, s. DAN., & Varberg, D. DAN. (2007). Perhitungan. Pendidikan Pearson.
7. Saenz, J. (2005). Kalkulus diferensial (Ed kedua.). Barquisimeto: Hypotenusa.
8. Thomas, g. B., & Bendung, m. D. (2006). Perhitungan: beberapa variabel. Pendidikan Pearson.