Sifat turunan parsial, perhitungan, latihan

Itu turunan parsial dari suatu fungsi dengan beberapa variabel independen adalah yang dicapai dengan mengambil turunan biasa di salah satu variabel, sementara yang lain dipertahankan atau diambil sebagai konstanta.

Turunan parsial dalam salah satu variabel, menentukan bagaimana fungsi bervariasi pada setiap titik, per unit perubahan variabel yang dimaksud. 

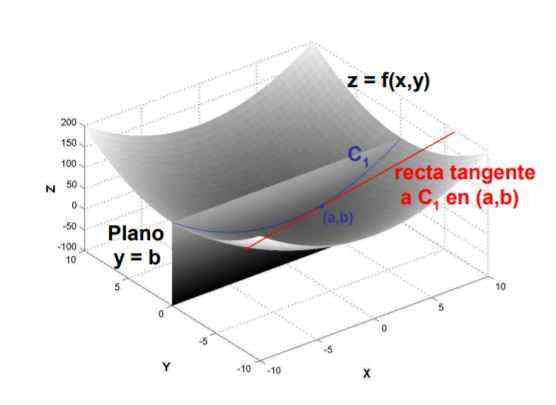Gambar 1. Kemiringan garis garis singgung ke kurva yang dibentuk oleh persimpangan bidang y = b dengan permukaan f (x, y) pada titik (a, b) adalah turunan parsial F sehubungan dengan x, dievaluasi pada titik itu. Sumber: UPM.adalah

Karena definisinya, turunan parsial dihitung dengan mengambil batas matematika dari hasil bagi antara variasi fungsi dan variasi variabel sehubungan dengan apa yang diturunkan, ketika perubahan yang terakhir cenderung nol.

Misalkan kasus fungsi F Itu tergantung pada variabel X Dan Dan, artinya setiap pasangan (X, y) A ditugaskan z: 

f: (x, y) → z .

Turunan parsial dari fungsi z = f (x, y), mengenai X didefinisikan sebagai:

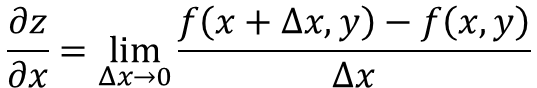
Sekarang, ada beberapa cara untuk menunjukkan turunan parsial suatu fungsi, misalnya:

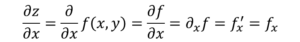
Perbedaan dengan turunan biasa, dalam hal notasi, adalah bahwa D derivasi diubah menjadi simbol ∂, dikenal sebagai "Jacobi D".

[TOC]

Sifat turunan parsial

Turunan parsial dari fungsi beberapa variabel, sehubungan dengan salah satunya, adalah turunan biasa dalam variabel tersebut dan menganggap sisanya sebagai tetap atau konstan. Untuk menemukan turunan parsial, aturan derivasi turunan biasa dapat digunakan.

Di bawah properti utama:

Dapat melayani Anda: faktor umum untuk istilah pengelompokan: contoh, latihan

Kontinuitas

Jika suatu fungsi f (x, y) memiliki turunan parsial di X Dan Dan pada intinya (Xo, saya) maka dapat dikatakan bahwa fungsinya terus menerus pada saat itu.

Aturan rantai

Sebuah fungsi f (x, y) Dengan turunan parsial kontinu di X Dan Dan, yang pada gilirannya tergantung pada parameter T melalui x = x (t) Dan y = y (t), Ini memiliki turunan biasa sehubungan dengan variabel T, yang dihitung oleh aturan rantai:

D_T Z = ∂_Xz d_Tx + ∂_Danz d_TDan

Properti Penutup atau Kunci

Turunan parsial sehubungan dengan salah satu variabel fungsi F dari dua atau lebih variabel (X, y, ...), Ini adalah fungsi lain G Dalam variabel yang sama, misalnya: 

G (x, y, ...) = ∂_Dan f (x, y, ...)

Yaitu, derivasi parsial adalah operasi yang berjalan dari r^N a r^N. Dalam hal itu dikatakan bahwa itu adalah a Operasi Tertutup.

Derivatif parsial berturut -turut

Turunan parsial berturut -turut dari fungsi beberapa variabel dapat didefinisikan, sehingga menimbulkan fungsi baru dalam variabel independen yang sama.

Jadilah fungsinya f (x, y). Derivatif berturut -turut berikut dapat didefinisikan:

F_Xx = ∂_XF ;  F_{Y y} = ∂_{Y y}F ; F_Xy = ∂_XyF Dan F_Yx = ∂_YxF

Dua yang terakhir dikenal sebagai Derivatif campuran karena mereka melibatkan dua variabel independen yang berbeda.

Teorema Schwarz

Menjadi fungsi f (x, y), didefinisikan sedemikian rupa sehingga turunan parsialnya adalah fungsi kontinu dalam subset terbuka R².

Jadi, untuk setiap pasangan (X, y) Bahwa mereka milik subset, turunan campuran identik:

∂_XyF = ∂_YxF

Pernyataan sebelumnya dikenal sebagai Teorema Schwarz.

Bagaimana turunan parsial dihitung?

Derivatif parsial dihitung mirip dengan turunan fungsi biasa dalam variabel independen tunggal. Ketika turunan parsial dari fungsi beberapa variabel diambil sehubungan dengan salah satunya, variabel lain diambil sebagai konstanta.

Dapat melayani Anda: setengah dari 15

Di bawah ini adalah beberapa contoh:

Contoh 1

Jadilah fungsinya:

f (x, y) = -3x² + 2 (dan - 3)²

Itu diminta untuk menghitung turunan parsial pertama sehubungan dengan X dan turunan parsial pertama sehubungan dengan Dan.

Prosedur

Untuk menghitung parsial F mengenai X, Telah diambil Dan sebagai konstan:

∂_XF = ∂_X(-3x² + 2 (dan - 3)² ) = ∂_X(-3x² )+ ∂_X(2 (dan - 3)² ) = -3 ∂_X(X²) + 0 = -6x.

Dan pada gilirannya, untuk menghitung turunan sehubungan dengan Dan Telah diambil X sebagai konstan:

∂_DanF = ∂_Dan(-3x² + 2 (dan - 3)² ) = ∂_Dan(-3x² )+ ∂_Dan(2 (dan - 3)² ) = 0 + 2 · 2 (y - 3) = 4y - 12.

Contoh 2

Tentukan turunan parsial urutan kedua:  ∂_Xxf, ∂_{Y y}f, ∂_YxF Dan ∂_XyF Untuk fungsi yang sama F Contoh 1.

Prosedur

Dalam hal ini, karena turunan parsial pertama sudah dihitung X Dan Dan (Lihat Contoh 1):

∂_XxF = ∂_X(∂_Xf) = ∂_X(-6x) = -6

∂_{Y y}F = ∂_Dan(∂_Danf) = ∂_Dan(4y - 12) = 4

∂_YxF = ∂_Dan(∂_Xf) = ∂_Dan(-6x) = 0

∂_XyF = ∂_X(∂_Danf) = ∂_X(4y - 12) = 0

Diamati itu ∂_YxF = ∂_XyF, dengan demikian memenuhi teorema Schwarz, karena fungsinya F dan turunan parsial urutan pertama semuanya adalah fungsi berkelanjutan R².

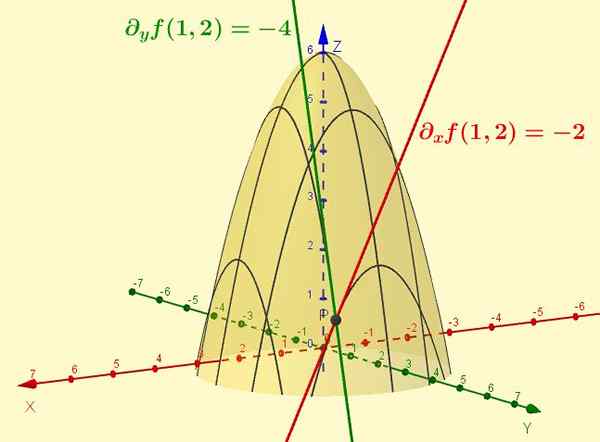
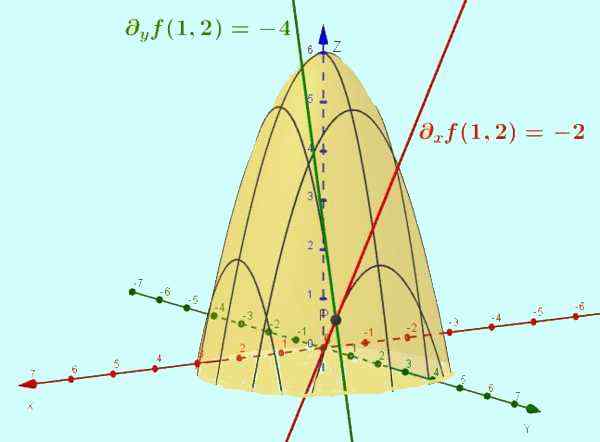Gambar 2. Fungsi z = f (x, y) = -x2 - y2 + 6 adalah permukaan yang ditunjukkan pada gambar. Turunan parsial sehubungan dengan x adalah kemiringan garis garis singgung kurva yang dihasilkan dari persimpangan permukaan tersebut dengan bidang y = ctte (kasus tertentu ditampilkan y = 2). Demikian pula bagian F sehubungan dengan dan merupakan kemiringan garis singgung ke persimpangan dengan x = 1, pada titik (1, 2, 1).

Latihan terpecahkan

Latihan 1

Jadilah fungsinya:

Dapat melayani Anda: Successsied Quadratic: Contoh, Aturan, dan Latihan Terselesaikan

f (x, y) = -x² - Dan² + 6

Temukan fungsi G (x, y) = ∂_XF  Dan H (x, y) = ∂_DanF.

Larutan

Turunan parsial F mengenai X, untuk mana variabelnya Dan Itu menjadi konstan:

G (x, y) = - 2x

Demikian pula, turunan parsial G mengenai Dan, sedang mengerjakan X konstan, menghasilkan fungsi H:

H (x, y) = -2y

Latihan 2 

Mengevaluasi intinya (1, 2) fungsi f (x, y) Dan G (x, y) Latihan 1. Menafsirkan hasilnya.

Larutan

Nilai diganti x = 1 Dan y = 2 memperoleh:

f (1,2) = -(1)² -(2)² + 6 = -5 + 6 = 1

Ini adalah nilai yang mengambil fungsi F ketika dievaluasi pada saat itu.

Fungsinya f (x, y) Ini adalah permukaan dua dimensi dan koordinat z = f (x, y) Itu adalah ketinggian fungsi untuk setiap pasangan (X, y). Saat pasangan diambil (1.2), Tinggi permukaan f (x, y) adalah Z = 1.

Fungsinya G (x, y) = - 2x mewakili bidang dalam ruang tiga dimensi yang persamaannya Z = -2x O baik -2x + 0 dan -z = 0.

Pesawat tersebut tegak lurus terhadap pesawat Xz Dan melewati titik (0, 0, 0). Saat dievaluasi di x = 1 Dan y = 2 Jadi Z = -2. Perhatikan bahwa nilainya z = g (x, y) Itu independen dari nilai yang ditetapkan untuk variabel Dan.

Di sisi lain, jika permukaan berpotongan f (x, y) Dengan pesawat y = c, dengan C konstan, Anda memiliki kurva di pesawat Zx: z = -x² - C² + 6.

Dalam hal ini turunan z mengenai X bertepatan dengan turunan parsial f (x, y) mengenai X: D_X Z = ∂_XF .

Saat mengevaluasi dalam pasangan (x = 1, y = 2) Turunan parsial pada saat itu ∂_XF (1.2) Itu ditafsirkan sebagai kemiringan garis garis singgung ke kurva z = -x² + 2 pada intinya (x = 1, y = 2) Dan nilai lereng ini -2.

Referensi

1. Ayres, f. 2000. Perhitungan. 5ed. MC Graw Hill.
2. Turunan parsial dari suatu fungsi dalam beberapa variabel. Pulih dari: bangunan.UPM.adalah.
3. Leithold, l. 1992. Perhitungan dengan geometri analitik. Harla, s.KE.
4. Purcell, e. J., VARBERG, D., & Rigdon, s. DAN. (2007). Perhitungan. Meksiko: Pendidikan Pearson.
5. Gorostizaga J. C. Turunan parsial. Pulih dari: ehu.Eus
6. Wikipedia. Turunan parsial. Pulih dari: is.Wikipedia.com.