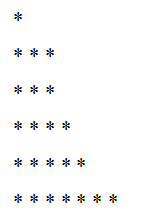Dekomposisi aditif

Itu dekomposisi aditif bilangan bulat positif adalah untuk mengekspresikannya sebagai jumlah dua atau lebih angka positif. Dengan demikian, kami memiliki angka 5 itu dapat mengekspresikannya sebagai 5 = 1+4, 5 = 2+3 atau 5 = 1+2+2. Masing -masing cara menulis nomor 5 adalah apa yang akan kita sebut dekomposisi aditif.

Jika kita memperhatikan, kita dapat melihat bahwa ekspresi 5 = 2+3 dan 5 = 3+2 mewakili komposisi yang sama; Keduanya memiliki angka yang sama. Namun, hanya untuk masalah kenyamanan biasanya ditulis masing -masing iklan yang mengikuti kriteria dari yang paling kecil ke yang terhebat.

Dekomposisi aditif

Sebagai contoh lain kita dapat mengambil nomor 27, yang dapat kita ungkapkan sebagai:

27 = 7+10+10

27 = 9+9+9

27 = 3+6+9+9

27 = 9+18

Dekomposisi Aditif adalah alat yang sangat berguna yang memungkinkan kita untuk memperkuat pengetahuan kita tentang sistem penomoran.

Dekomposisi aditif kanonik

Ketika kita memiliki jumlah lebih dari dua angka, bentuk tertentu untuk membusuknya adalah dalam kelipatan 10, 100, 1000, 10.000, dll., itu menebusnya. Cara menulis angka ini disebut dekomposisi aditif kanonik. Misalnya, angka 1456 dapat menguraikannya sebagai berikut:

1456 = 1000 + 400+ 50 + 6

Jika kami memiliki nomor 20 846 295, dekomposisi aditif kanonik Anda adalah:

20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.

Berkat dekomposisi ini, kita dapat melihat bahwa nilai digit yang diberikan diberikan oleh posisi yang ditempati. Mari kita ambil sebagai contoh angka 24 dan 42:

24 = 20 + 4

42 = 40 +2

Di sini kita dapat melihat bahwa dalam 24 2 memiliki nilai 20 unit dan pada 4 nilai 4 unit; Di sisi lain, di 42 4 memiliki nilai 40 unit dan 2 dari dua unit. Dengan demikian, meskipun kedua angka menggunakan angka yang sama, nilainya sama sekali berbeda dengan posisi yang mereka tempati.

Dapat melayani Anda: x kuadrat

Aplikasi

Salah satu aplikasi yang dapat kami berikan pada dekomposisi aditif adalah dalam jenis demonstrasi tertentu, di mana sangat berguna untuk melihat bilangan bulat positif sebagai jumlah orang lain.

Contoh Teorema

Mari kita ambil contoh teorema berikut dengan demonstrasi masing -masing.

- Jadilah z jumlah utuh 4 digit, maka z dapat dibagi dengan 5 jika gambarnya sesuai dengan unit adalah nol atau lima.

Demonstrasi

Mari kita ingat apa itu Divisibilitas. Jika kita memiliki bilangan bulat "a" dan "b", kita mengatakan bahwa "A" membagi "b" jika ada bilangan bulat "c" sedemikian rupa sehingga b = a*c.

Salah satu sifat divisibilitas memberi tahu kita bahwa jika "A" dan "B" dapat dibagi antara "C", maka pengurangan "A-B" juga adalah.

Jadilah z jumlah utuh 4 digit; Oleh karena itu, kita dapat menulis ke Z dan Z = ABCD.

Menggunakan dekomposisi aditif kanonik kita harus:

Z = A*1000 + B*100 + C*10 + D

Jelas bahwa A*1000 + B*100 + C*10 dapat dibagi antara 5. Inilah sebabnya kami memiliki bahwa Z dapat dibagi antara 5 jika z - (A*1000 + B*100 + C*10) dapat dibagi antara 5.

Tetapi z - (a*1000 + b*100 + c*10) = d dan d adalah angka angka tunggal, jadi satu -satunya cara untuk dibagi antara 5 adalah 0 atau 5.

Oleh karena itu, z dapat dibagi antara 5 jika d = 0 atau d = 5.

Perhatikan bahwa jika z memiliki n digit, demonstrasi persis sama, itu hanya berubah yang sekarang kita tulis z = a₁KE₂… KE_N Dan tujuannya adalah untuk membuktikannya_N adalah nol atau lima.

Partisi

Kami mengatakan bahwa partisi bilangan bulat positif adalah cara di mana kami dapat menulis angka sebagai jumlah bilangan bulat positif.

Dapat melayani Anda: Radio Konvergensi: Definisi, Contoh dan Latihan Diselesaikan

Perbedaan antara dekomposisi aditif dan partisi adalah bahwa, sementara yang pertama dicari bahwa setidaknya dapat dipecah menjadi dua atau lebih, dalam partisi pembatasan ini.

Jadi, kami memiliki yang berikut:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+2+2

Di atas adalah partisi dari 5.

Artinya, kita memiliki bahwa semua dekomposisi aditif adalah partisi, tetapi tidak semua partisi tentu merupakan dekomposisi aditif.

Dalam teori angka, teorema mendasar dari aritmatika menjamin bahwa setiap bilangan bulat dapat ditulis secara unik sebagai produk sepupu.

Ketika partisi dipelajari, tujuannya adalah untuk menentukan berapa banyak cara bilangan bulat positif dapat ditulis sebagai jumlah bilangan bulat lainnya. Oleh karena itu kami mendefinisikan fungsi partisi seperti yang disajikan di bawah ini.

Definisi

Fungsi partisi p (n) didefinisikan sebagai jumlah cara di mana bilangan bulat positif dapat ditulis sebagai jumlah bilangan bulat positif.

Kembali ke contoh 5, kita harus:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+1+3

5 = 1+2+2

5 = 1+1+1+2

5 = 1+1+1+1+1

Dengan cara ini, p (5) = 7.

Grafik

Baik partisi dan dekomposisi aditif dari angka n dapat diwakili secara geometris.  Misalkan kita memiliki dekomposisi aditif n. Dalam dekomposisi ini addend dapat diperbaiki sehingga anggota jumlah dipesan dari yang paling sedikit ke yang terbesar. Jadi, ada baiknya:

n = a₁ + ke₂ + ke₃ +... + a_R dengan

ke₁ ≤ a₂ ≤ a₃ ≤ ... ≤ a_R.

Kita dapat grafik mengatakan dekomposisi sebagai berikut: Di baris pertama kita menandai a₁-poin, kemudian di berikut ini kami menandai₂-poin, dan seterusnya sampai mencapai_R.

Dapat melayani Anda: Ketimpangan segitiga: demonstrasi, contoh, latihan terpecahkan

Mari kita ambil sebagai contoh nomor 23 dan dekomposisi berikutnya:

23 = 5 + 4 + 7 + 3 + 1 +3

Kami memesan dekomposisi ini dan kami memiliki:

23 = 1 + 3 + 3 + 4+ 5 + 7

Grafik yang sesuai adalah:

Demikian juga, jika kita membaca grafik ini sebagai gantinya secara vertikal secara horizontal, kita dapat memperoleh dekomposisi yang mungkin berbeda dari sebelumnya. Dalam contoh 23, yang berikut ini menonjol:

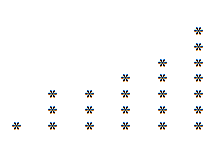
Jadi kita memiliki 23 itu kita juga bisa menulisnya sebagai:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.