Persamaan diagram moody, untuk apa, aplikasi

Dia Diagram murung Ini terdiri dari serangkaian kurva yang ditarik pada kertas logaritmik, yang digunakan untuk menghitung faktor gesekan yang ada dalam aliran cairan turbulen melalui saluran melingkar.

Dengan faktor gesekan F Hilangnya energi gesekan dievaluasi, nilai penting untuk menentukan kinerja pompa yang tepat yang mendistribusikan cairan seperti air, bensin, mentah.

Pipa di tingkat industri. Sumber: Pixabay.

Untuk mengetahui energi dalam aliran fluida yang diperlukan dan dinding pipa.

[TOC]

Persamaan untuk energi cairan gerak

Di antara dua bagian pipa, yang dilapisi sebagai 1 Dan 2, Dimungkinkan untuk menetapkan keseimbangan berikut, yang merupakan perluasan persamaan Bernoulli: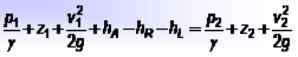Di mana:

- P₁ Dan P₂ adalah tekanan di setiap titik,

- z₁ Dan z₂ adalah ketinggian sehubungan dengan titik referensi,

- v₁ Dan v₂ adalah kecepatan cairan masing -masing,

- H_KE Itu adalah energi yang ditambahkan oleh pompa, H_R Itu adalah energi yang diambil oleh perangkat seperti mesin, dan H_L Ini mencakup kehilangan energi fluida karena gesekan antara ini dan dinding pipa, serta kerugian kecil lainnya.

Nilai dari H_L Itu dihitung menggunakan persamaan Darcy-Weisbach:

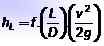
Di mana L Itu adalah panjang pipa, D Itu adalah diameter dalamnya, v Itu adalah kecepatan cairan dan G Itu adalah nilai percepatan gravitasi. Dimensi H_L Mereka panjang, dan biasanya unit -unit yang diwakili adalah meter atau kaki.

-Faktor gesekan dan nomor Reynolds

Menghitung F Persamaan empiris yang diperoleh dari data eksperimental dapat digunakan. Perlu untuk membedakan apakah itu cairan dalam rezim laminar atau rezim turbulen. Untuk rezim laminar F Itu mudah dievaluasi:

F = 64/n_R

Di mana N_R Itu adalah nomor Reynolds, yang nilainya tergantung pada rezim di mana cairan berada. Kriteria adalah:

Aliran Laminar: N_R < 2000 el flujo es laminar; Flujo turbulento N_R > 4000; Rezim transisi: 2000 < N_R < 4000

Nomor Reynolds (tanpa dimensi) pada gilirannya tergantung pada kecepatan fluida v, Diameter internal pipa D dan viskositas kinematik N dari cairan, yang nilainya diperoleh dengan tabel:

Dapat melayani Anda: Gerakan bujursangkar yang dipercepat secara seragam: Karakteristik, formula

N_R = v.D /n

Persamaan Colebrook

Untuk aliran yang bergejolak, persamaan yang paling diterima dalam pipa tembaga dan kaca adalah Cyril Colebrook (1910-1997), tetapi memiliki ketidaknyamanan itu F Itu tidak eksplisit:

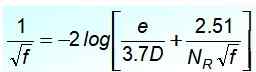
Dalam persamaan ini hasil bagi e/d Itu adalah kekasaran relatif pipa dan N_R Itu adalah nomor Reynolds. Saat mengamatinya dengan hati -hati, diperhatikan bahwa tidak mudah untuk pergi F Di sisi kiri kesetaraan, jadi tidak nyaman untuk perhitungan langsung.

Colebrook sendiri menyarankan pendekatan ini yang eksplisit, berlaku dengan beberapa keterbatasan:

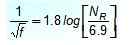
Untuk apa?

Diagram Moody berguna untuk menemukan faktor gesekan F Termasuk dalam persamaan Darcy, mengingat fakta bahwa dalam persamaan Colebrook tidak mudah untuk diungkapkan F langsung dalam hal nilai -nilai lain.

Penggunaannya menyederhanakan mendapatkan nilai F, dengan berisi representasi grafis dari F dalam fungsi N_R Untuk nilai -nilai kekasaran relatif yang berbeda pada skala logaritmik.

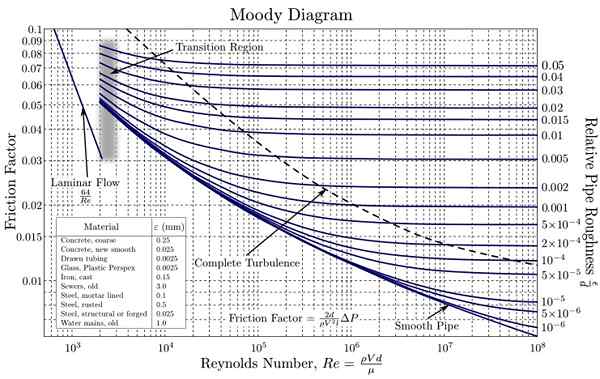Diagram murung. Sumber: https: // unggah.Wikimedia.org/wikipedia/commons/d/d9/moody_en.SVG

Kurva ini telah dibuat dari data eksperimental dengan berbagai bahan yang biasa digunakan dalam pembuatan pipa. Penggunaan skala logaritmik untuk F untuk N_R Itu perlu, karena mereka mencakup berbagai nilai yang sangat luas. Dengan cara ini, grafik nilai -nilai orde besar yang berbeda difasilitasi.

Grafik pertama persamaan Colebrook diperoleh oleh Engineer Hunter Rouse (1906-1996) dan tak lama setelah itu dimodifikasi oleh Lewis F. Moody (1880-1953) dalam cara yang digunakan saat ini.

Ini digunakan untuk pipa bundar dan tidak lingkaran, cukup untuk menggantikan diameter hidrolik untuk ini.

Bagaimana cara melakukannya dan bagaimana itu digunakan?

Seperti yang dijelaskan di atas, diagram moody terbuat dari banyak data eksperimental, disajikan secara grafis. Berikut langkah -langkah untuk menggunakannya:

- Hitung nomor Reynolds N_R Untuk menentukan apakah alirannya laminar atau turbulen.

- Hitung kekasaran relatif dengan persamaan Dan_R = E/D, Di mana Dan Ini adalah kekasaran absolut material dan D adalah diameter internal pipa. Nilai -nilai ini diperoleh dengan tabel.

- Sekarang sudah tersedia Dan_R Dan N_R, Proyeksi secara vertikal sampai mencapai kurva yang sesuai dengan Dan_R diperoleh.

- Proyek secara horizontal dan ke kiri untuk membaca nilai F.

Contoh akan dengan mudah memvisualisasikan bagaimana diagram digunakan.

Dapat melayani Anda: kalsium fluoride (caf2): struktur, sifat, penggunaan

-Contoh 1

Tentukan faktor gesekan air pada 160º F yang mengalir pada laju 22 kaki/s dalam saluran yang terbuat dari zat besi tempa yang tidak dilapisi dan diameter internal 1 inci.

Larutan

Data yang diperlukan (ditemukan di tabel):

Viskositas kinematik air pada 160 ºF: 4.38 x 10^-6 kaki²/S

Kekasaran absolut dari besi tempa tidak tertutup: 1.5 x 10 ^-4 kaki

Langkah pertama

Jumlah Reynolds dihitung, tetapi tidak sebelum melewati diameter internal 1 inci pada kaki:

1 inci = 0.0833 kaki

N_R = (22 x 0.0833)/ 4.38 x 10^-6= 4.18 x 10 ⁵

Menurut kriteria yang ditunjukkan sebelum itu adalah aliran turbulen, maka diagram murung memungkinkan faktor gesekan yang sesuai untuk diperoleh, tanpa harus menggunakan persamaan Colleebrook.

Tahap kedua

Anda harus menemukan kekasaran relatif:

Dan_R = 1.5 x 10 -4 / 0.0833 = 0.0018

Langkah ketiga

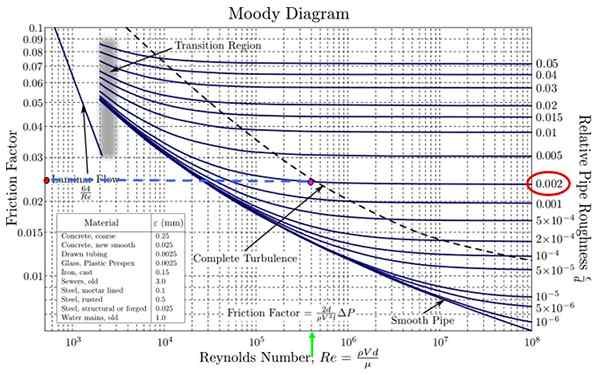
Dalam diagram moody yang disediakan itu perlu. Tidak ada yang sesuai persis pada 0.0018 Tapi ada satu yang banyak mendekati, 0.002 (oval merah dari gambar).

Secara bersamaan, angka Reynolds yang sesuai dicari pada sumbu horizontal. Nilai yang paling mirip dengan 4.18 x 10 ⁵ adalah 4 x 10 ⁵ (Panah hijau pada gambar). Persimpangan keduanya adalah titik fuchsia.

Langkah Keempat

Proyek kiri ke garis putus -putus kiri dan sampai ke titik oranye. Sekarang perkirakan nilainya F, Mempertimbangkan bahwa divisi tidak memiliki ukuran yang sama karena itu adalah skala logaritmik baik di horizontal dan sumbu vertikal.

Diagram murung yang disediakan dalam gambar tidak memiliki divisi horizontal yang baik, jadi nilai F di 0.024 (antara 0.02 dan 0.03 Tapi itu tidak setengah tapi sedikit kurang).

Ada kalkulator online yang menggunakan persamaan Colleebrook. Salah satunya (lihat referensi) nilai yang disediakan 0.023664639 untuk faktor gesekan.

Aplikasi

Diagram moody dapat diterapkan untuk menyelesaikan tiga jenis masalah, asalkan cairan dan kekasaran pipa absolut diketahui:

- Perhitungan penurunan tekanan atau perbedaan tekanan antara dua titik, memasok panjang pipa, perbedaan tinggi antara dua titik yang akan dipertimbangkan, kecepatan dan diameter internal pipa.

Dapat melayani Anda: gerakan pendular

- Penentuan aliran, diketahui panjang dan diameter pipa, ditambah penurunan tekanan spesifik.

- Evaluasi diameter pipa saat panjang, aliran dan tekanan penurunan antara titik yang diketahui diketahui.

Masalah tipe pertama diselesaikan secara langsung dengan menggunakan diagram, sedangkan tipe kedua dan ketiga memerlukan penggunaan paket komputasi. Misalnya, pada orang -orang dari tipe ketiga, jika diameter pipa tidak diketahui, angka Reynolds tidak dapat dievaluasi secara langsung, atau kekasaran relatif.

Salah satu cara untuk menyelesaikannya adalah dengan mengasumsikan diameter internal awal dan dari sana secara berturut -turut menyesuaikan nilai untuk mendapatkan penurunan tekanan yang ditentukan dalam masalah.

-Contoh 2

Ini memiliki air pada suhu 160 ° F yang diparkir di sepanjang pipa 1 inci dalam diameter besi tempa yang tidak tertutup, dengan kecepatan 22 kaki/s. Tentukan perbedaan tekanan yang disebabkan oleh gesekan dan daya pemompaan yang diperlukan untuk mempertahankan aliran dalam bentangan pipa horizontal L = 200 kaki panjangnya.

Larutan

Data yang diperlukan: Percepatan gravitasi adalah 32 kaki/s² ; Berat spesifik air pada 160 ºF adalah γ = 61.0 lb-force/kaki³

Ini adalah pipa dari contoh yang diselesaikan 1, oleh karena itu faktor gesekan sudah diketahui F, yang diperkirakan 0.0024. Nilai ini dibawa ke persamaan Darcy untuk mengevaluasi kerugian gesekan:

Daya pemompaan yang diperlukan adalah:

W = v. KE. (P₁ - P₂)

Dimana a adalah penampang tabung: a = p. (D²/4) = p. (0.0833²/4) kaki² = 0.00545 kaki²

W = 22 kaki /s . 2659.6 lb-force / kaki². 0.00545 kaki²= 318.9 lb-force . kaki

Kekuatan lebih baik diekspresikan dalam watt, yang diperlukan faktor konversi:

1 watt = 0.737 lb-force . kaki

Oleh karena itu kekuatan yang dibutuhkan untuk mempertahankan aliran adalah W = 432.7 w

Referensi

1. Cimbala, c. 2006. Mekanika Cairan, Fundamental dan Aplikasi. MC. Bukit Graw. 335-342.
2. Franzini, J. 1999. Mekanika fluida dengan aplikasi sedang dalam bidang teknik. MC. Bukit Graw.176-177.
3. LMNO Engineering. Faktor Kalkulator Gesekan Moody. Pulih dari: lmnoeng.com.
4. Mott, r.  2006. Mekanika Cairan. 4. Edisi. Pendidikan Pearson. 240-242.
5. Kotak alat teknik. Diagram murung. Dipulihkan dari: EngineeringToolbox.com
6. Wikipedia. Bagan Moody. Pulih dari: di.Wikipedia.org