Beban radial bagaimana dihitung, latihan terpecahkan

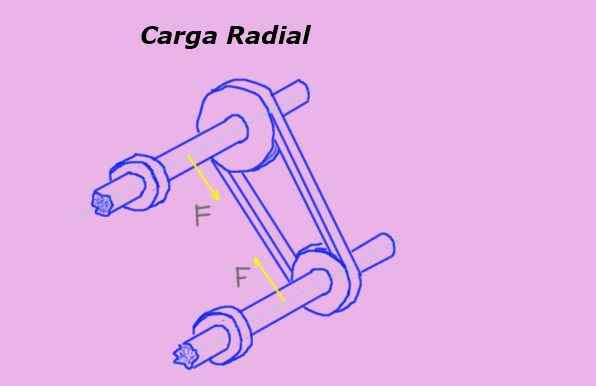
Itu Beban radial Itu adalah kekuatan yang dilakukan secara tegak lurus terhadap sumbu simetri suatu objek dan yang garis tindakannya melewati sumbu ini. Misalnya, sabuk pada katrol memaksakan beban radial pada bantalan atau bantalan sumbu yang sama.

Pada Gambar 1 panah kuning mewakili gaya radial pada sumbu karena tegangan sabuk yang melewati katrol.

Gambar 1. Beban radial pada kapak katrol. Sumber: Made sendiri.

Unit ukuran beban radial dalam sistem internasional atau jika itu adalah Newton (n). Tetapi unit kekuatan lainnya juga digunakan untuk mengukurnya, seperti kekuatan kilogram (kg-f) dan kekuatan pound (lb-f).

[TOC]

Bagaimana itu dihitung? 

Untuk menghitung nilai beban radial dalam elemen struktur, langkah -langkah berikut harus diikuti:

- Buat diagram gaya pada setiap elemen.

- Terapkan persamaan yang menjamin keseimbangan translasi; yaitu, jumlah semua kekuatan adalah nol.

- Pertimbangkan persamaan torsi atau momen sehingga keseimbangan rotasi terpenuhi. Dalam hal ini jumlah semua torsi harus nol.

- Hitung kekuatan untuk mengidentifikasi beban radial yang bertindak di masing -masing elemen.

Latihan terpecahkan

-Latihan 1

Gambar berikut menunjukkan katrol yang melaluinya katrol tegang lewat dengan tegangan t. Katrol dipasang pada sumbu yang bertumpu pada dua chumaceras. Pusat salah satu dari mereka berada di jarak l₁ dari tengah katrol. Di ujung lain adalah chumacera lainnya, di kejauhan l₂.

Dapat melayani Anda: higroskopisitas: konsep, zat higroskopis, contoh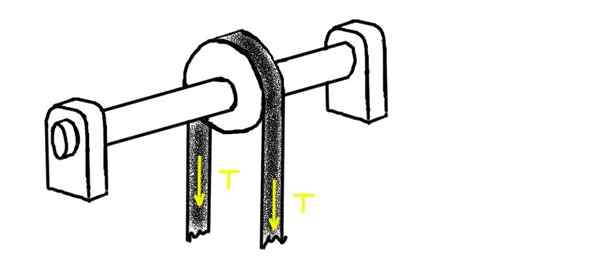Gambar 2. Katrol yang melaluinya tali tegang lewat. Sumber: Made sendiri.

Tentukan beban radial pada masing -masing chumaceras, dengan asumsi bahwa berat sumbu dan katrol cukup rendah dari tegangan yang diterapkan.

Ambil nilai untuk tegangan strap 100 kg-f dan untuk jarak l₁= 1 m dan l₂= 2 m.

Larutan

Pertama -tama, diagram kekuatan yang bekerja pada sumbu dibuat.

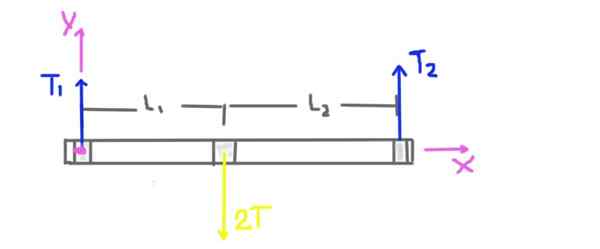Gambar 3. Olahraga memaksa diagram 1.

Tegangan katrol adalah T, tetapi beban radial pada sumbu pada posisi katrol adalah 2t. Berat sumbu dan katrol tidak diperhitungkan karena pernyataan masalah memberi tahu kita bahwa itu jauh lebih rendah daripada tegangan yang diterapkan pada sabuk.

Reaksi radial dari dukungan dukungan disebabkan oleh gaya radial atau beban T1 dan T2. Jarak L1 dan L2 dari dukungan ke pusat katrol juga ditunjukkan dalam diagram.

Sistem koordinat juga ditampilkan. Torsi atau momen total pada sumbu akan dihitung mengambil sebagai pusat asal sistem koordinat dan akan positif dalam arah z.

Kondisi keseimbangan

Kondisi keseimbangan sekarang ditetapkan: jumlah nol yang sama dan jumlah torsi sama dengan nol.

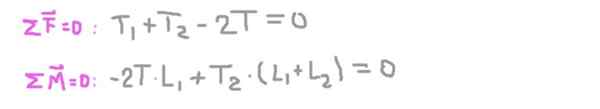
Dari persamaan kedua reaksi radial pada sumbu pada dukungan 2 (t₂), mengganti yang pertama dan membersihkan reaksi radial pada sumbu pada dukungan 1 (t₁).

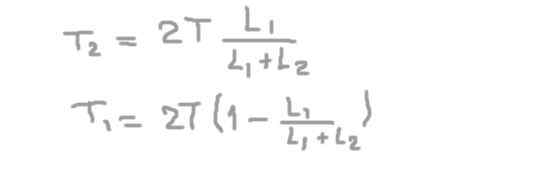Jika kami mengganti data numerik, kami memperoleh beban radial atau paksa pada sumbu pada posisi dukungan 1 adalah:

T₁= (2/3) t = 66,6 kg-f

Itu dapat melayani Anda: Kurva Kalibrasi: Untuk apa itu, bagaimana melakukannya, contoh

Dan beban radial pada sumbu dalam dukungan dukungan 2 adalah:

T₂= (4/3) t = 133.3 kg-f.

Latihan 2

Gambar berikut menunjukkan sistem yang terdiri dari tiga katrol A, B, C semua radio r. Katrol dihubungkan oleh sabuk yang memiliki tegangan T.

Axes A, B, C PASS Bantalan yang dilumasi. Pemisahan antara pusat sumbu A dan B adalah 4 kali jari -jari R. Demikian pula, pemisahan antara sumbu B dan C juga 4R.

Tentukan beban radial pada sumbu katrol A dan B, dengan asumsi bahwa tegangan sabuk adalah 600N.

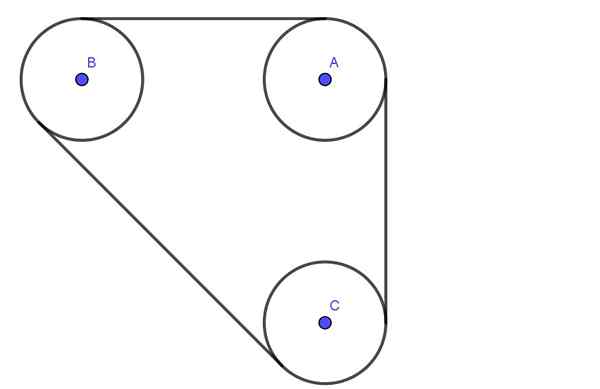Gambar 4. Sistem katrol. Latihan 2. (Elaborasi sendiri)

Larutan

Itu dimulai dengan menggambar diagram kekuatan yang bekerja pada katrol A dan B. Pada yang pertama Anda memiliki kedua ketegangan T₁ dan T₂, serta kekuatan f_KE Bahwa bantalan diberikan pada poros katrol.

Demikian pula, pada katrol b Anda memiliki ketegangan t₃ , T₄ dan kekuatan f_B Bahwa bantalan diberikan pada sumbu yang sama. Beban radial pada sumbu katrol A adalah gaya f_KE dan beban radial pada B adalah gaya f_B.

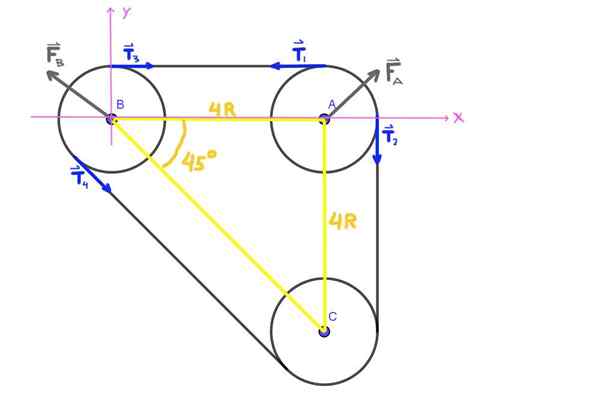Gambar 5. Diagram Pasukan, Latihan 2. (Elaborasi sendiri)

Sebagai sumbu A, B, C membentuk segitiga isorektang, sudut ABC adalah 45 °.

Semua ketegangan t₁ , T₂ , T₃ , T₄ ditunjukkan pada gambar memiliki modul t yang sama, yang merupakan tegangan sabuk.

Kondisi keseimbangan untuk katrol a

Sekarang kita menulis kondisi keseimbangan untuk katrol yang tidak lain adalah jumlah dari semua kekuatan yang bertindak atas katrol a harus batal.

Memisahkan komponen x dan y dari gaya dan menambahkan (secara vektor) pasangan persamaan skalar berikut diperoleh:

Dapat melayani Anda: Titan (satelit)

F_KEX - T = 0; F_KEDAN - T = 0

Persamaan ini mengarah pada kesetaraan berikut: f_Kapak = F_OH = T.

Oleh karena itu beban radial memiliki besarnya yang diberikan oleh:

F_KE = (T² + t²)^1/2 = 2^1/2∙ t = 1.41 ∙ t = 848.5 n. 45 ° arah. 

Kondisi keseimbangan untuk katrol b

Demikian pula, kami menulis kondisi keseimbangan untuk katrol b. Untuk komponen x Anda memiliki: f_BX + T + t ∙ cos45 ° = 0

Dan untuk komponen y: f_BDAN + T ∙ sen45 ° = 0

Dengan demikian:

F_Bx = - t (1+2^-1/2) dan f_Oleh = -T ∙ 2^-1/2

Artinya, besarnya beban radial pada katrol B adalah:

F_B = ((1+2^-1/2) ² + 2^-1)^1/2∙ t = 1.85 ∙ t = 1108.66 N dan alamatnya 135 °.

Referensi

1. Bir F, Johnston E, DeWolf J, Mazurek, D. Mekanika Bahan. Edisi Kelima. 2010. MC Graw Hill. 1-130.
2. Gere J, goodno, b. Mekanika Bahan. Edisi Kedelapan. Pembelajaran Cengage. 4-220.
3. Giancoli, d. 2006. Fisika: Prinsip dengan aplikasi. 6^Tth Ed. Prentice Hall. 238-242.
4. Hibbeler R. Mekanika Bahan. Edisi Kedelapan. Prentice Hall. 2011. 3-60.
5. Valera Negrete, J. 2005. Catatan Fisika Umum. Unam. 87-98.