Dinamika Contoh Sistem Partikel, Latihan

Itu Dinamika sistem partikel Ini terdiri dari penerapan hukum Newton dari gerakan ke serangkaian partikel, yang dapat bijaksana (partikel dapat dihitung) atau menjadi bagian dari objek yang diperluas, dalam hal ini sistem ini kontinu.

Untuk menjelaskan pergerakan sistem partikel, tidak nyaman untuk menganalisis masing -masing secara terpisah dan melihat kekuatan apa yang bertindak padanya. Sebaliknya, titik representatif dari set didefinisikan, disebut Pusat Massa.

Menggambarkan pergerakan pusat massa menawarkan panorama yang sangat sukses dari gerakan global set, juga memungkinkan untuk menerapkan hukum Newton yang dianalogikan ketika objek dianggap sebagai partikel tanpa dimensi.

Model terakhir ini, disebut model partikel, Adalah baik untuk menggambarkan terjemahan dan juga ketika tidak perlu mempertimbangkan dimensi objek. Tetapi benda biasa adalah ukuran dan jika mereka juga memiliki gerakan rotasi, perlu untuk memperhitungkan titik -titik di mana kekuatan diterapkan.

[TOC]

Contoh

Bumi dan bulan

Ilustrasi Bumi dan Bulan

Satu set partikel diskrit m₁, M₂, M₃... yang pada akhirnya bergerak sehubungan dengan asal sistem koordinat, karena beberapa kekuatan yang dihasilkan yang bekerja pada mereka adalah contoh yang baik dari sistem partikel.

Bumi dapat dianggap sebagai satu partikel dan bulan lain, maka keduanya merupakan sistem 2 partikel di bawah aksi gaya gravitasi matahari.

Objek yang diperluas

Seseorang, hewan atau objek lingkungan apa pun, juga dapat dianggap sebagai sistem partikel, hanya bahwa ini sangat kecil, sehingga seseorang tidak dapat menghitung satu per satu. Ini adalah sistem yang berkelanjutan, tetapi dengan mempertimbangkan pertimbangan tertentu, perlakuannya sama dengan sistem yang bijaksana.

Itu bisa melayani Anda: apa entalpi pelatihan? (Dengan latihan)

Berikut detailnya.

Pusat massa sistem partikel

Untuk memulai studi tentang sistem partikel, Anda harus menemukan pusat massa (cm), yang merupakan titik di mana seluruh massa sistem terkonsentrasi.

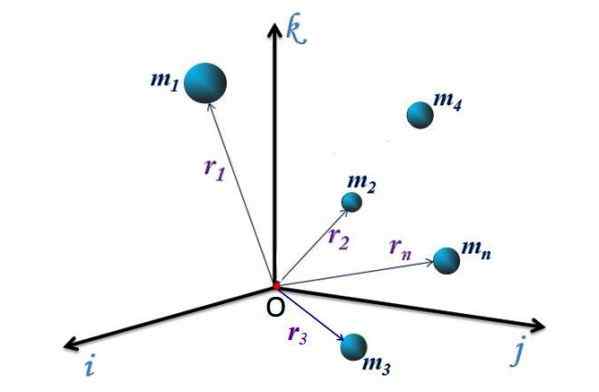
Gambar 1. Sistem partikel dalam sistem referensi XYZ. Sumber: f. Zapata.

Untuk sistem diskrit dari Gambar 1, dengan N partikel, masing -masing memiliki posisi vektor yang diarahkan dari asal atau sistem koordinat ke titik p (x, y, z) di mana partikel berada. Vektor -vektor ini dilambangkan sebagai R₁, R₂, R₃.. R_N.

Koordinat CM dihitung dengan persamaan berikut:

Di mana masing -masing massa set direpresentasikan sebagai m₁, M₂, M₃... M_N. Perhatikan bahwa jumlah ∑ m_yo Itu setara dengan massa total m dari set. Jika sistemnya berkelanjutan, ringkasan diganti dengan integral.

Masing -masing alamat tegak lurus diwakili oleh vektor unit yo, J Dan k, Oleh karena itu, vektor posisi CM, dilambangkan R_Cm, Itu dapat diungkapkan dengan:

R_Cm = x_Cm yo + Dan_Cm J + z_Cm k

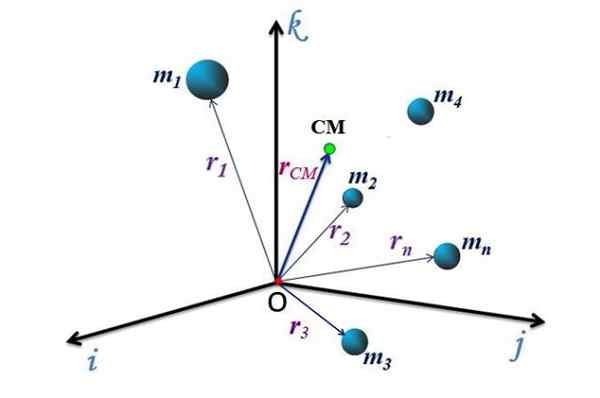Gambar 2. Lokasi pusat massa sistem partikel. Sumber: f. Zapata.

Gerakan CM

Setelah lokasi pusat massa diketahui, persamaan gerakan yang diketahui diterapkan. Kecepatan CM adalah yang pertama berasal dari posisi sehubungan dengan waktu:

Dalam hal ini, sistem memiliki jumlah total gerakan P yang dihitung sebagai produk dari massa total sistem dan kecepatan pusat massa:

Itu dapat melayani Anda: lintasan fisik: karakteristik, jenis, contoh dan latihan

P = M ∙v_Cm

Atau, jumlah total sistem sistem dapat dihitung secara langsung:

P = m₁v₁ + M₂v₂ + M₃v₃ +.. . = ∑ m_yo v_yo

Sedangkan percepatan CM adalah kecepatan yang diturunkan:

Kekuatan pada CM

Kekuatan yang bekerja pada sistem partikel bisa:

• Kekuatan internal, karena interaksi antara partikel yang sama.
• Kekuatan eksternal, disebabkan oleh agen eksternal ke sistem.

Karena kekuatan internal disajikan oleh pasangan, dengan besarnya dan arah yang sama, tetapi indera yang berlawanan, menurut hukum ketiga Newton, dipenuhi bahwa:

∑ F_int = 0

Oleh karena itu, kekuatan internal tidak mengubah pergerakan keseluruhan, tetapi mereka sangat penting untuk menentukan energi internal.

Jika sistem terisolasi dan tidak ada kekuatan eksternal, menurut hukum pertama Newton, pusat massa sedang istirahat atau bergerak dengan gerakan bubur seragam yang seragam. Kalau tidak, pusat pengalaman massa yang diberikan oleh:

∑ F_ext = M ∙ke_Cm

Dimana m adalah massa total sistem. Persamaan sebelumnya dapat ditulis seperti ini:

Dan itu berarti bahwa kekuatan eksternal setara dengan variasi sementara dalam jumlah gerakan, cara lain untuk mengekspresikan hukum kedua Newton dan yang sama digunakan oleh fisikawan Inggris yang terkenal dalam bukunya Prinsip.

Olahraga diselesaikan

Pusat massa sistem 2 partikel berada pada sumbu x pada saat tertentu, pada posisi x = 2.0 m dan bergerak dengan kecepatan 5.0 m/s ke arah yang sama dan positif. Jika salah satu partikel adalah asal dan yang lain, dari massa 0.1 kg, beristirahat di x = 8.0 m, Hitung:

Dapat melayani Anda: diamagnetisme: bahan, aplikasi, contoh

a) massa partikel yang berasal.

b) Jumlah gerakan sistem

c) Kecepatan apa yang merupakan partikel yang berasal dari asalnya?

Solusi untuk

Dari persamaan untuk posisi pusat massa:

R_Cm = x_Cm yo + Dan_Cm J + z_Cm K = 2.0 m yo

Karena CM hanya memiliki koordinat x, persamaan trio pertama yang sebelumnya diberikan digunakan:

Koordinat sekarang diganti, jika partikel dilambangkan pada asal seperti nomor 1 dan yang lainnya seperti nomor 2, data numerik adalah:

X₁ = 0 m, x₂ = 8.0 m, m₂ = 0.1 kg, x_Cm = 2.0 m

Tetap:

= 0.3kg

Solusi b

Jumlah pergerakan sistem dihitung oleh:

P = M ∙v_Cm

Total massa M sama dengan:

M = 0.3 kg + 0.1 kg = 0.4 kg

Karena itu:

P = 0.4 kg ∙ 5.0 m/s yo = 2 kg.MS yo

Solusi c

Dari persamaan untuk P dari sistem dua bagian, jelas v₁, Karena data lain diketahui, karena pernyataan itu mengatakan bahwa partikel 2 sedang istirahat, oleh karena itu: oleh karena itu:

v₂ = 0 

DAN P Itu seperti:

P = m₁v₁

v₁ = P / M₁ = 2 kg.MS yo / 0.3kg = 6.67 m/s yo

Referensi

1. Universitas Duke. Sistem partikel. Pulih dari: webhome.Phy.Duke.Edu.
2. Rex, a. 2011. Dasar -dasar fisika. Pearson.
3. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7. Ed. Pembelajaran Cengage.
5. Tipler, hlm. (2006) Fisika untuk Sains dan Teknologi. Edisi ke -5. Volume 1. Editorial dikembalikan.