Konsep jarak jauh Euclidian, rumus, perhitungan, contoh

Itu Jarak Euclidian Ini adalah angka positif yang menunjukkan pemisahan yang dimiliki dua titik di ruang di mana aksioma dan teorema geometri Euclid terpenuhi.

Jarak antara dua titik A dan B ruang Euclidian adalah panjang vektor AB Milik satu -satunya garis yang melewati titik -titik ini.

Gambar 1 . Ruang Euclidean unidimensional yang dibentuk oleh garis (OX). Beberapa titik di ruang ini, koordinat dan jarak mereka ditampilkan. (Disiapkan oleh Ricardo Pérez).

Ruang yang kita rasakan dan di mana kita memindahkan manusia adalah ruang tiga dimensi (3-D), di mana aksioma dan teorema geometri euclide terpenuhi. Di ruang ini ada dua subruang (rencana) dan satu -dimensi (lurus) (lurus) (lurus).

Ruang Euclidean dapat dari satu dimensi (1-D), dua dimensi (2-D), tiga dimensi (3-D) atau N dimensi (N-D).

Ini adalah titik dalam ruang satu -dimensi X milik garis berorientasi (OX), arah dari atau ke x adalah alamat positif. Untuk menemukan titik -titik di baris ini, sistem Cartesian yang terdiri dari penetapan setiap titik garis digunakan angka.

[TOC]

Rumus

Jarak Euclidian D (A, B) didefinisikan antara titik A dan B, yang terletak di garis, seperti akar kuadrat dari kuadrat perbedaan koordinat x:

D (a, b) = √ ((xb - xa)^2)

Definisi ini menjamin bahwa: jarak antara dua titik selalu merupakan jumlah positif. Dan bahwa jarak antara A dan B sama dengan jarak antara B dan A.

Gambar 1 menunjukkan ruang Euclidian satu -dimensi yang dibentuk oleh garis (OX) dan beberapa titik pada garis itu. Setiap titik memiliki koordinat:

Poin A memiliki koordinat xa = 2.5, koordinat b xb = 4 dan titik C koordinat xc = -2.5

Itu dapat melayani Anda: probabilitas frekuensi: konsep, bagaimana itu dihitung dan contoh

D (a, b) = √ ((4 - 2.5) 2) = 1.5

D (b, a) = √ ((2.5 - 4) 2) = 1.5

D (a, c) = √ ((-2.5 - 2.5) 2) = 5.0

Jarak euclidian dalam dua dimensi

Ruang Euclide Dua -Dimensi adalah pesawat. Titik -titik bidang Euclidian memenuhi aksioma geometri Euclid, misalnya:

- Pada dua poin, satu baris lulus. 

- Tiga titik di pesawat membentuk segitiga yang sudut internalnya selalu tambahkan 180º.

- Dalam segitiga persegi panjang, kuadrat dari hipotenuse sama dengan jumlah kotak dari kakinya.

Dalam dua dimensi suatu titik memiliki koordinat x dan y. 

Misalnya titik P memiliki koordinat (xp, yp) dan titik yang terkoordinasi (xq, yq).

Jarak Euclidean antara titik P dan Q didefinisikan dengan formula berikut:

D (p, q) = √ ((xq - xp)^2 + (yq - yp)^2)

Perlu dicatat bahwa rumus ini setara dengan teorema Pythagoras, seperti yang ditunjukkan pada Gambar 2.

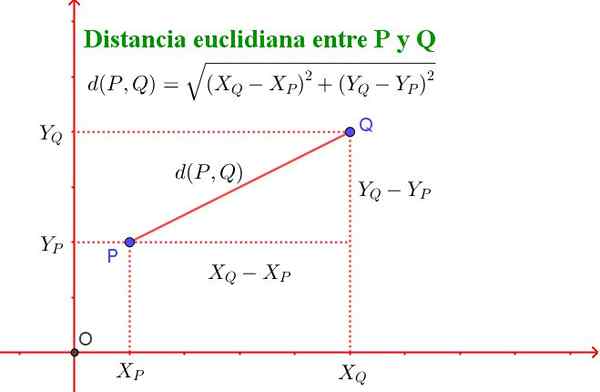Gambar 2. Jarak antara dua titik P dan Q pesawat memenuhi teorema Pythagoras. (Disiapkan oleh Ricardo Pérez).

Permukaan nonuclidian

Tidak semua dua ruang -dimensi memenuhi geometri Euclidean. Permukaan bola adalah ruang dua dimensi.

Sudut segitiga pada permukaan bola tidak menambah 180º dan dengan ini teorema Pythagoras tidak terpenuhi, oleh karena itu permukaan bola tidak memenuhi aksioma euclid.

Jarak euclidian dalam dimensi n

Konsep koordinat dapat diperluas ke dimensi yang lebih besar:

- Pada titik 2-D P memiliki koordinat (XP, YP)

- Dalam 3-D titik yang memiliki koordinat (xq, yq, zq)

- Pada titik 4-D R akan memiliki koordinat (XR, YR, ZR, WR)

- Dalam N-D poin P akan memiliki koordinat (P1, P2, P3, ..., PN)

Dapat melayani Anda: grafik bar: karakteristik, untuk apa, contohnya

Jarak antara dua titik P dan Q dari ruang Euclidian N-dimensi dihitung dengan rumus berikut:

D (p, q) = √ ((q1 - p1)^2 +(q2 - p2)^2 +... +(qn - pn)^2)

Tempat geometris dari semua titik yang dalam ruang Euclidean N-dimensi yang sama dari Equidists dari titik p tetap lain (pusat) membentuk hypersfera N-dimensional.

Cara menghitung jarak euclidian

Di bawah ini adalah jarak antara dua titik yang terletak di ruang tiga dimensi Euclidian dihitung.

Asumsikan titik A dari koordinat cartesian x, y, z yang diberikan oleh :( 2, 3, 1) dan titik B dari koordinat b :( -3, 2, 2).

Anda ingin menentukan jarak antara titik -titik ini, di mana hubungan umum digunakan:

D (a, b) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )

D (a, b) = √ (25 + 1 + 1) = √ (27) = √ (9 *3) = 3 √ (3) = 5.196

Contoh

Ada dua poin p dan q.  Titik P untuk Koordinat Kartesia x, y, z yang diberikan oleh P :( 2, 3, 1) dan titik Q koordinat q :( -3, 2, 1).

Itu diminta untuk menemukan koordinat titik tengah m dari segmen [PQ] yang menghubungkan kedua titik. 

Larutan:

Diasumsikan bahwa titik M yang tidak diketahui memiliki koordinat (x, y, z).

Karena m adalah titik rata -rata [pq] harus dipenuhi bahwa d (p, m) = d (q, m), jadi itu juga harus dipenuhi d (p, m)^2 = d (q, m)^^ 2:

(X - 2)^2 + (y - 3)^2 + (z - 1)^2 = (x - (-3))^2 + (y - 2)^2 + (z - 1)^2

Seperti dalam kasus ini, istilah ketiga adalah sama dalam dua anggota ekspresi sebelumnya disederhanakan untuk:

Dapat melayani Anda: konstanta absolut

(X - 2)^2 + (y - 3)^2 = (x + 3)^2 + (y - 2)^2 

Kemudian ada persamaan dengan dua yang tidak diketahui x dan y. Persamaan lain diperlukan untuk menyelesaikan masalah.

Poin M milik garis yang melewati titik P dan Q, yang dapat kita hitung sebagai berikut:

Pertama adalah Direktur Vektor PQ dari garis: PQ = = .

Kemudian PM = Op + ke PQ, Di mana Op Itu adalah posisi vektor titik p dan ke Itu adalah parameter yang termasuk dalam bilangan real. 

Persamaan sebelumnya dikenal sebagai persamaan vektor garis, yang dalam koordinat Cartesian mengadopsi sebagai berikut:

= + a =

Sama dengan komponen yang sesuai adalah:

X - 2 = 2 - 5 a; Dan - 3 = 3 -a; Z - 1 = 0

Artinya x = 4 - 5a, y = 6 - a, akhirnya z = 1.

Itu diganti dalam ekspresi kuadratik yang berhubungan x ke y:

(4 - 5a - 2)^2 + (6 - a - 3)^2 = (4 - 5a + 3)^2 + (6 - a - 2)^2

Itu disederhanakan:

(2 - 5a)^2 + (3 -a)^2 = (7 - 5a)^2 + (4 - a)^2

Sekarang berkembang:

4 + 25 a^2 - 20a + 9 + a^2 - 6a = 49 + 25 a^2 - 70a + 16 + a^2 - 8a

Itu disederhanakan, membatalkan istilah serupa di kedua anggota:

4 - 20a + 9 - 6a = 49 - 70a + 16 - 8a

Parameter A:

52 a = 49 + 16 - 4 - 9 = 52 Menghasilkan bahwa a = 1.

Artinya x = 4 - 5, y = 6 - 1, akhirnya z = 1.

Akhirnya kami mendapatkan koordinat Cartesian dari titik tengah M segmen [PQ]:

G: (-1, 5, 1).

Referensi

1. Lehmann c. (1972) Geometri analitik. Uteha.
2. Superprof. Jarak antara dua titik. Pulih dari: superprof.adalah
3. Unam. Jarak antara varietas sublinear terkait. Pulih dari: prometheus.Matem.Unam.MX/
4. Wikipedia. Jarak Euclidian. Pulih dari: is.Wikipedia.com
5. Wikipedia. Ruang Euclidean. Pulih dari: is.Wikipedia.com