Distribusi formula normal, karakteristik, contoh, olahraga

Itu distribusi normal o Distribusi Gaussian adalah distribusi probabilitas dalam variabel kontinu, di mana fungsi kepadatan probabilitas dijelaskan oleh fungsi eksponensial argumen kuadratik dan negatif, yang menghasilkan bentuk yang terkelupas.

Nama distribusi normal berasal dari fakta bahwa distribusi ini adalah yang diterapkan pada jumlah situasi terbesar di mana beberapa variabel acak kontinu terlibat dalam kelompok atau populasi tertentu.

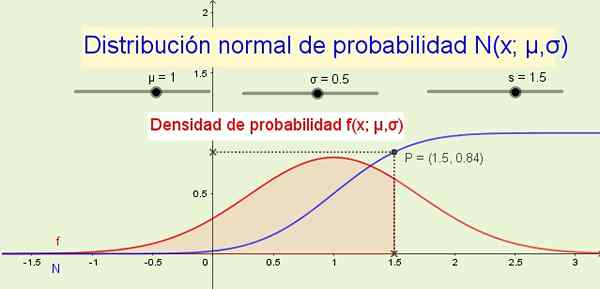
Gambar 1. Distribusi normal n (x; μ, σ) dan kepadatan probabilitasnya f (s; μ, σ). (Elaborasi sendiri)

Sebagai contoh di mana distribusi normal diterapkan: ketinggian pria atau wanita, variasi sejauh beberapa magnitudo fisik atau dalam fitur psikologis atau sosiologis yang terukur seperti hasil bagi intelektual atau kebiasaan konsumsi dari produk tertentu.

Di sisi lain, ini disebut Gaussian Distribution atau Gauss Bell, karena jenius matematika Jerman inilah yang dikreditkan dengan penemuannya untuk penggunaan yang ia berikan untuk deskripsi kesalahan statistik pengukuran astronomi pada tahun 1800.

Namun, diklaim bahwa distribusi statistik ini sebelumnya diterbitkan oleh ahli matematika hebat lainnya yang berasal dari Prancis, seperti halnya Abraham de Moivre, pada tahun 1733.

[TOC]

Rumus

Ke fungsi distribusi normal dalam variabel kontinu X, Dengan parameter μ Dan σ Itu dilambangkan dengan:

N (x; μ, σ)

Dan secara eksplisit ditulis seperti ini:

N (x; μ, σ) = ∫_-∞^X f (s; μ, σ) ds

Di mana f (u; μ, σ) Ini adalah fungsi kepadatan probabilitas:

f (s; μ, σ) = (1/(σ√ (2π)) exp ( - s²/(2σ²)

Konstanta yang melipatgandakan fungsi eksponensial dalam fungsi kepadatan probabilitas disebut konstan normalisasi, dan telah dipilih sedemikian rupa sehingga:

N (+∞, μ, σ) = 1

Ekspresi sebelumnya memastikan bahwa probabilitas variabel acak X berada di antara -∞ dan +∞ baik 1, yaitu probabilitas 100%.

Parameter μ Itu adalah rata -rata aritmatika dari variabel acak kontinu x dan σ Deviasi standar atau akar kuadrat dari varians dari variabel yang sama. Dalam hal itu μ = 0 Dan σ = 1 Anda memiliki standar distribusi standar atau distribusi normal yang khas: 

N (x; μ = 0, σ = 1)

Karakteristik distribusi normal

1- Jika variabel statistik acak mengikuti distribusi kepadatan probabilitas normal f (s; μ, σ), Sebagian besar data dikelompokkan di sekitar nilai rata -rata μ Dan mereka tersebar di sekitar mereka sehingga tepat di antara data ada di antara μ - σ Dan μ + σ. 

Dapat melayani Anda: frekuensi absolut: rumus, perhitungan, distribusi, contoh

2- standar deviasi σ Itu selalu positif.

3- Bentuk fungsi kepadatan F Itu menyerupai lonceng, jadi fungsi ini sering disebut Gaussian Bell atau Gaussian Function. 

4- Dalam distribusi Gaussian rata-rata, median dan mode bertepatan.

5- Titik belok dari fungsi kepadatan probabilitas ditemukan tepat μ - σ Dan μ + σ.

6- Fungsi F adalah simetris sehubungan dengan sumbu yang melewati nilai rata-rata μ Dan Anda memiliki nol asimtotik untuk x ⟶ +∞ dan x ⟶ -∞.

7- Nilai yang lebih tinggi σ dispersi yang lebih besar, kebisingan atau data menjauhkan di sekitar nilai rata -rata. Artinya lebih besar σ Bentuk lonceng lebih terbuka. Alih-alih σ Kecil menunjukkan bahwa dadu berenang ke rata -rata dan bentuk lonceng lebih tertutup atau runcing.

8- Fungsi distribusi N (x; μ, σ) menunjukkan probabilitas bahwa variabel acak kurang dari atau sama dengan X. Misalnya, pada Gambar 1 (di atas) probabilitas p bahwa variabel X kurang dari atau sama dengan 1.5 adalah 84% dan sesuai dengan area di bawah fungsi kepadatan probabilitas f (x; μ, σ) Dari -∞ ke X.

Interval kepercayaan

9- Jika data mengikuti distribusi normal, maka 68,26% dari ini berada di antara μ - σ Dan μ + σ.

10- 95,44% dari data yang mengikuti distribusi normal adalah antar μ - 2σ Dan μ + 2σ.

11- 99,74% dari data yang mengikuti distribusi normal adalah antar μ - 3σ Dan μ + 3σ.

12- Jika variabel acak X Ikuti distribusi N (x; μ, σ), Lalu variabel

Z = (x - μ) / σ  Ikuti distribusi normal standar  N (z; 0,1).

Perubahan variabel X ke z Ini disebut standardisasi atau tipuan dan sangat berguna pada saat menerapkan tabel distribusi standar ke data yang mengikuti distribusi non-standar normal.

Aplikasi distribusi normal

Untuk menerapkan distribusi normal, perlu melalui perhitungan integral dari kepadatan probabilitas, yang dari sudut pandang analitik tidak mudah dan tidak selalu tersedia program komputer yang memungkinkan perhitungan numeriknya. Untuk tujuan ini, tabel Nilai Standar atau Tipik digunakan, yang tidak lebih dari distribusi normal dalam kasus ini μ = 0 dan σ = 1.

Dapat melayani Anda: Operasi gabungan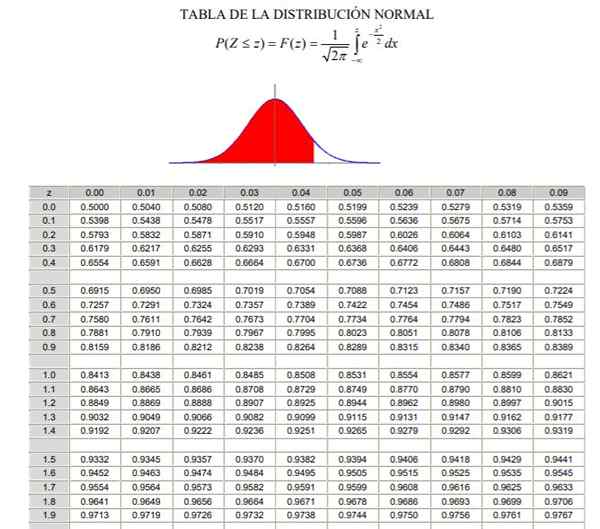Tabel Distribusi Normal Ditambahkan (Bagian 1/2) 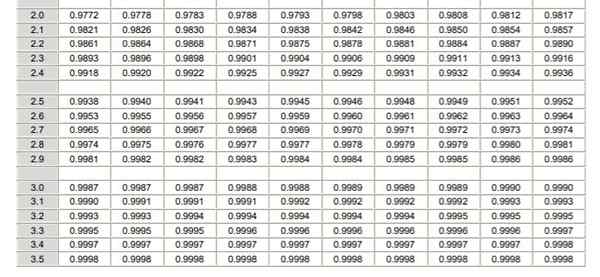Tabel Distribusi Normal Ditambahkan (Bagian 2/2)

Perlu dicatat bahwa tabel ini tidak termasuk nilai negatif. Namun, menggunakan sifat simetri dari fungsi kepadatan probabilitas Gaussian, nilai yang sesuai dapat diperoleh. Dalam latihan terselesaikan yang ditunjukkan di bawah penggunaan tabel ditunjukkan dalam kasus ini.

Contoh

Asumsikan bahwa Anda memiliki set data acak X yang mengikuti distribusi rata -rata normal 10 dan standar deviasi 2. Itu diminta untuk menemukan probabilitas bahwa:

a) Variabel acak x kurang dari atau sama dengan 8.

b) kurang dari atau sama dengan 10.

c) variabel x itu di bawah 12.

d) Probabilitas bahwa nilai x adalah antara 8 dan 12.

Larutan:

a) Untuk menjawab pertanyaan pertama yang harus Anda hitung:

N (x; μ, σ)

Dengan x = 8, μ = 10 Dan σ = 2. Kami menyadari bahwa ini adalah integral yang tidak memiliki solusi analitik dalam fungsi dasar, tetapi solusinya diekspresikan sesuai dengan fungsi kesalahan ERF (x).

Di sisi lain, ada kemungkinan memecahkan integral dengan cara numerik, yang merupakan kalkulator, spreadsheet, dan program komputer seperti yang dilakukan oleh Geogebra Do. Gambar berikut menunjukkan solusi numerik yang sesuai dengan kasus pertama:

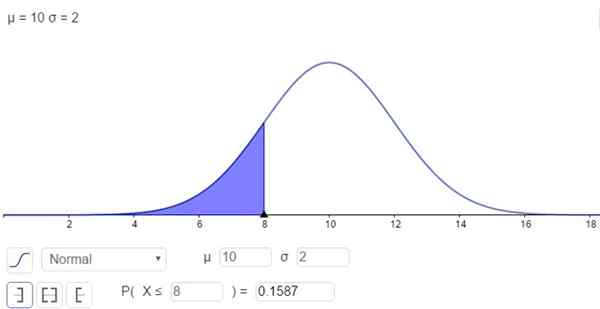Gambar 2. Kepadatan probabilitas f (x; μ, σ). Area teduh mewakili P (x ≤ 8). (Elaborasi sendiri)

Dan jawabannya adalah probabilitas bahwa X di bawah 8 adalah:

P (x ≤ 8) = n (x = 8; μ = 10, σ = 2) = 0,1587

b) Dalam hal ini tentang menemukan probabilitas bahwa variabel acak x berada di bawah rata -rata yang dalam hal ini bernilai 10. Jawabannya tidak memerlukan perhitungan apa pun, karena kita tahu bahwa setengah dari data berada di bawah rata -rata dan setengah lainnya di atas rata -rata. Karena itu, jawabannya adalah:

P (x ≤ 10) = n (x = 10; μ = 10, σ = 2) = 0,5

c) Untuk menjawab pertanyaan ini, Anda harus menghitung N (x = 12; μ = 10, σ = 2), yang dapat dilakukan dengan kalkulator yang memiliki fungsi statistik atau dengan perangkat lunak seperti Geogebra:

Dapat melayani Anda: pembagi 8: apa itu dan penjelasan yang mudah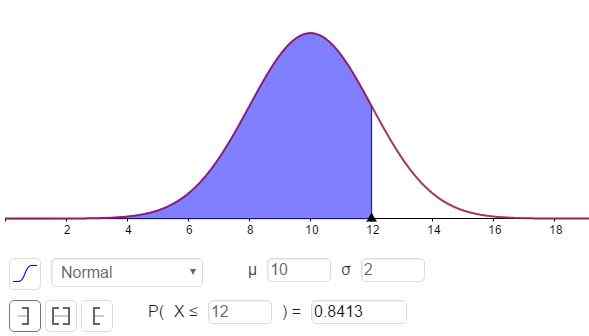Gambar 3. Kepadatan probabilitas f (x; μ, σ). Area teduh mewakili P (x ≤ 12). (Elaborasi sendiri)

Respons terhadap Bagian C dapat dilihat pada Gambar 3 dan adalah:

P (x ≤ 12) = n (x = 12; μ = 10, σ = 2) = 0,8413.

d) Untuk menemukan probabilitas bahwa variabel acak adalah antara 8 dan 12 kita dapat menggunakan hasil bagian A dan C sebagai berikut:

P (8 ≤ x ≤ 12) = p (x ≤ 12) - p (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26.

Olahraga diselesaikan

Harga rata -rata saham perusahaan adalah $ 25 dengan standar deviasi $ 4. Tentukan probabilitas bahwa:

a) Suatu tindakan memiliki biaya kurang dari $ 20.

b) yang memiliki biaya lebih besar dari $ 30.

c) harganya antara $ 20 dan $ 30.

Gunakan tabel distribusi normal yang ditandai untuk menemukan jawabannya.

Larutan:

Untuk memanfaatkan tabel, perlu untuk pindah ke variabel yang dinormalisasi atau ditiru:

$ 20 dalam variabel standar sama z = ($ 20 - $ 25) / $ 4 = -5/4 = -1,25 dan 

$ 30 dalam variabel standar sama z = ($ 30 - $ 25) / $ 4 = +5/4 = +1.25.

a) $ 20 setara dengan -1,25 dalam variabel standar, tetapi tabel tidak memiliki nilai negatif, jadi kami menempatkan nilai +1.25 yang menunjukkan nilai 0,8944.

Jika nilai ini dikurangi 0,5 hasilnya akan menjadi luas antara 0 dan 1,25 yang, omong -omong, identik (dengan simetri) ke area antara -1.25 dan 0. Hasil pengurangan adalah 0,8944 - 0,5 = 0,3944 yang merupakan luas antara -1.25 dan 0.

Tetapi daerah yang menarik dari -∞ hingga -1,25 yang akan menjadi 0,5 -0,3944 = 0,1056. Oleh karena itu disimpulkan bahwa probabilitas bahwa suatu tindakan di bawah $ 20 adalah 10,56%.

b) $ 30 dalam variabel yang ditiru z adalah 1,25. Untuk nilai ini dalam tabel muncul angka 0.8944 yang sesuai dengan area dari -∞ hingga +1.25. Area antara +1.25 y +∞ adalah (1 - 0.8944) = 0.1056. Dengan kata lain, probabilitas bahwa tindakan berharga lebih dari $ 30 adalah 10,56%.

c) Probabilitas bahwa suatu tindakan memiliki biaya antara $ 20 dan $ 30 akan dihitung sebagai berikut:

100% -10,56% - 10,56% = 78,88%

Referensi

1. Statistik dan probabilitas. Distribusi normal. Diperoleh dari: Projectescartes.org
2. Geogebra. Geogebra klasik, perhitungan probabilitas. Pulih dari Geogebra.org
3. Mathworks. Distribusi Gauss. Pulih dari: is.Mathworks.com
4. Mendenhall, w. 1981. Statistik untuk Administrasi dan Ekonomi. 3. edisi. Grup Editorial Iberoamerica.
5. Stat Trek. Ajari diri Anda sendiri statistik. Distribusi racun. Pulih dari: stattrek.com,
6. Triola, m. 2012. Statistik dasar. 11. Ed. Pendidikan Pearson.
7. Universitas Vigo. Distribusi kontinu utama. Pulih dari: anapg.situs web.Uvigo.adalah
8. Wikipedia. Distribusi normal. Pulih dari: is.Wikipedia.org