Distribusi seragam melanjutkan karakteristik, contoh, aplikasi
- 4419
- 442
- Miss Marion Graham
Variabel acak memiliki a Distribusi seragam kontinu Jika probabilitas mengambil nilai, dalam interval terbatas [a, b], adalah sama untuk setiap sub-interval dengan panjang yang sama.
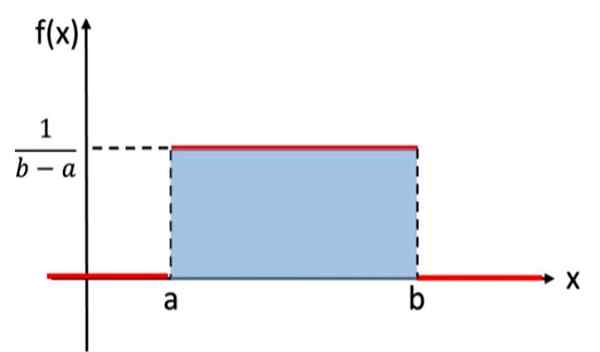
Distribusi ini analog dengan distribusi seragam diskrit, yang ditugaskan untuk setiap hasil percobaan acak probabilitas yang sama, tetapi dalam hal ini variabel yang akan dipertimbangkan adalah kontinu. Misalnya, percobaan yang terdiri dari pemilihan bilangan real acak, antara nilai A dan B, mengikuti distribusi yang seragam. Di sini Anda memiliki grafik:
Gambar 1. Grafik fungsi kepadatan dari distribusi seragam yang dinormalisasi terus menerus Dalam notasi matematika, distribusi seragam kontinu memiliki fungsi kepadatan yang didefinisikan sebagai fungsi pada potongan atau pada bagian, yang dapat ditulis sebagai:
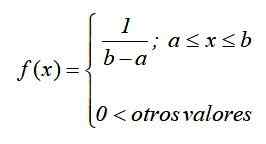
Grafik fungsi ini, dikenal sebagai Fungsi kurva atau kepadatan, Itu adalah persegi panjang, sehingga distribusi seragam kontinu juga dikenal sebagai distribusi persegi panjang Dan itu adalah distribusi berkelanjutan yang paling sederhana.
Area di bawah grafik distribusi probabilitas sama dengan 1 dan selalu mengambil nilai positif. Distribusi seragam memenuhi kriteria ini. Tidak perlu mengintegrasikan secara langsung untuk memverifikasi bahwa area tersebut adalah 1, karena luas persegi panjang yang diarsir pada Gambar 1 dapat dihitung menggunakan rumus:
Area = basis x tinggi = (b - a) x [1/(b - a)] = 1
Mengetahui area di bawah kurva kepadatan sangat penting, karena ada hubungan antara area dan probabilitas terjadinya suatu peristiwa, yang untuk distribusi ini ditentukan pada bagian berikut.
Karakteristik distribusi seragam kontinu
Distribusi seragam kontinu ditandai olehnya:
Fungsi kepadatan
Biarkan x menjadi variabel acak kontinu, yang termasuk dalam interval [a, b], lalu:
Itu dapat melayani Anda: transformasi linier: properti, apa saja penggunaan, jenis, contoh=\frac1b-a)
Fungsi distribusi
Dengan menggunakan fungsi distribusi, probabilitas bahwa variabel acak x mengambil nilai x dari nilai yang mungkin dari interval [a, b] dihitung. Untuk distribusi berkelanjutan, umumnya dihitung dengan cara ini:
=\int_a^xf(x)dx)
Dalam kasus distribusi seragam kontinu, probabilitas tersebut f (x) setara dengan area persegi panjang yang alasnya (x-a) dan tingginya (b-a):
=\int_a^x\left&space;(\frac1b-a&space;\right&space;)dx=\fracx-ab-a)
Secara matematis, jika f (x) = pr (x = x) Fungsi berikut ditetapkan oleh bagian, sesuai dengan hasil sebelumnya:
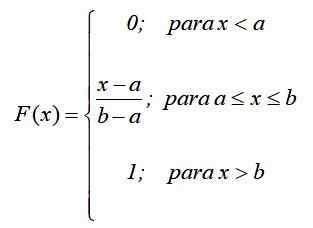
Dengan cara ini, apa yang telah dikatakan sebelumnya: probabilitas hanya tergantung pada nilai (x-a) dan tidak pada lokasinya dalam interval [a, b]. Grafik fungsi distribusi adalah:
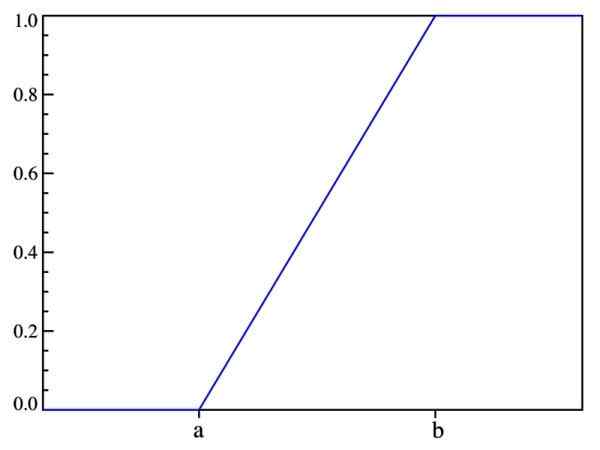Gambar 2. Grafik fungsi distribusi f (x). Sumber: Wikimedia Commons. Nilai yang diharapkan, varians, dan standar deviasi
Setelah melakukan banyak percobaan dengan variabel acak kontinu, nilai rata -rata disebut nilai yang diharapkan, Itu dilambangkan sebagai E (x) dan dihitung dengan integral berikut:
=\int_a^bxf(x)=\int_a^b\left&space;(\frac1b-a&space;\right&space;)xdx=\left&space;(\frac1b-a&space;\right&space;)\frac(b^2-a^2)2=\fraca+b2)
V (x) = e (x2) - MANTAN)2
Karena itu:
=\left&space;[\int_a^bx^2f(x)dx&space;\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2=\left&space;[\int_a^bx^2\left&space;(\fracb-a2&space;\right&space;)&space;dx\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2)
=\frac(b-a)^212)
D (x) = √ V (x)
=\sqrt\frac(b-a)^212)
Median, mode, simetri, dan curtosis
Dapat dengan mudah diverifikasi bahwa median, yang merupakan nilai sentral dari distribusi seragam, sama dengan rata -rata, dan karena tidak ada nilai yang diulang lebih dari yang lain, karena semua sama -sama mungkin dalam interval [a, b ], mode tidak ada.
Sedangkan untuk simetri, distribusi seragam adalah simetris dan curtosis, yang merupakan sejauh mana nilai -nilai di sekitar pusat terkonsentrasi adalah -6/5.
Dapat melayani Anda: apa 7 elemen keliling?Contoh
Berbagai situasi dapat dimodelkan melalui distribusi berkelanjutan, dan dengan demikian memprediksi perilaku mereka. Berikut beberapa contoh:
Contoh 1
Perusahaan yang menyediakan layanan listrik menyediakan tingkat tegangan terdistribusi secara merata, antara 123.0 V dan 125.0 v. Ini berarti bahwa dalam bidikan domestik dimungkinkan untuk mendapatkan nilai tegangan apa pun yang termasuk dalam interval itu.
Kemudian, seperti yang terlihat di atas, grafik fungsi kepadatan adalah persegi panjang merah:
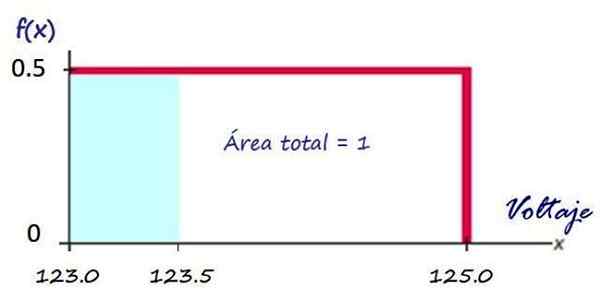Gambar 3. Fungsi kepadatan untuk tegangan yang disampaikan oleh perusahaan listrik. Sumber: f. Zapata. Menghitung probabilitas memiliki tegangan dalam interval yang diberikan sangat mudah, misalnya, berapa probabilitas bahwa perusahaan akan mengirim tegangan kurang dari 123.5 v?
Probabilitas ini setara dengan area persegi panjang yang diarsir dengan warna biru:
P (x<123.5) = (123.5 −123.0)x 0.5 = 0.25
Dan berapa probabilitas bahwa tegangan yang dikirim lebih besar dari 124.0 v?
Karena total area sama dengan 1, probabilitas yang dicari adalah:
P (x> 124.0 V) = 1 - (1 × 0.5) = 0.5
Masuk akal, sejak 124.0 justru nilai di tengah interval.
Contoh 2
Variabel acak tertentu x memiliki distribusi yang seragam dalam interval [0,100]. Menentukan:
a) probabilitas bahwa nilai x kurang dari 22.
b) probabilitas bahwa x mengambil nilai antara 20 dan 35.
c) nilai yang diharapkan, varians dan standar deviasi distribusi ini.
Menjawab
Ini ditentukan mirip dengan contoh sebelumnya, tetapi pertama -tama kita harus menentukan ketinggian persegi panjang, mengingat bahwa total area harus sama dengan 1:
Area = 100 × tinggi = 1
Oleh karena itu persegi panjang memiliki ketinggian yang sama dengan 1/100 = 0.01
Dapat melayani Anda: decagon: biasa, tidak teratur, properti, contohP (x<22) = 22×0.01 = 0.22
Jawaban b
Probabilitas yang diminta setara dengan area persegi panjang yang lebarnya (35 - 20) dan tingginya 0.01:
P (22 Jika Anda lebih suka pergi langsung ke fungsi distribusi di atas, maka Anda hanya perlu mengganti nilai di: P (20≤x≤35) = f (35) -f (20) Dengan f (x) diberikan oleh: F (x) = (x-a) / (b-a) Nilai yang akan diperkenalkan adalah: A = 0 B = 100 F (35) = (35-0) / (100-0) = 0.35 F (20) = (20-0) / (100-0) = 0.dua puluh P (20≤x≤35) = 0.35-0.20 = 0.limabelas Nilai yang diharapkan adalah: E (x) = (a+b)/2 = (100+0)/2 = 50 Variannya adalah: V (x) = (b-a)2/12 = (100-0)2/12 = 833.33 Dan deviasi standar adalah: D (x) = √833.33 = 28.87 Distribusi ini berguna saat proses simulasi statistik dilakukan atau saat bekerja di acara yang frekuensinya reguler. Beberapa bahasa pemrograman menghasilkan angka acak antara 0 dan 1, dan seperti yang dapat dilihat dari contoh sebelumnya, distribusi probabilitas yang diikuti adalah seragam. Dalam hal ini interval untuk dipertimbangkan adalah [0,1]. Jika Anda memiliki eksperimen di mana peristiwa tersebut memiliki keteraturan, seperti yang dijelaskan di atas, pada prinsipnya, Anda dapat menugaskan masing -masing probabilitas kejadian yang sama. Dalam hal ini, model probabilistik distribusi seragam memberikan informasi untuk analisis. Distribusi seragam juga digunakan dalam pembulatan perbedaan antara nilai yang diamati dan nilai nyata dari suatu variabel, dengan asumsi distribusi kesalahan yang seragam dalam interval yang diberikan, sesuai dengan pembulatan, biasanya -0,5 ke +0.5.Jawaban c
Aplikasi
Angka acak
Pengambilan sampel distribusi sewenang -wenang
Rounding kesalahan
Referensi