Distribusi diskrit
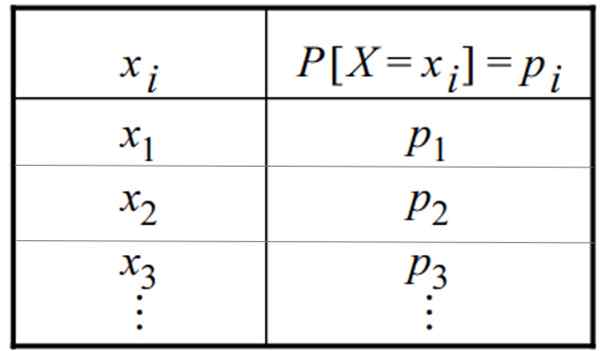
- 3959
- 1151
- Tommie Smith
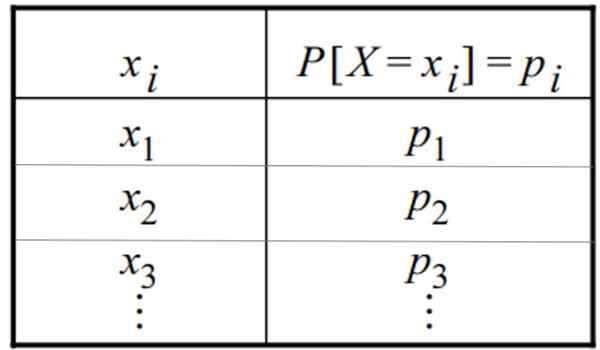 Tabel distribusi probabilitas yang bijaksana. Sumber: f. Zapata
Tabel distribusi probabilitas yang bijaksana. Sumber: f. Zapata Apa itu distribusi yang bijaksana?
A distribusi yang bijaksana probabilitas adalah fungsi f (xyo) yang menetapkan untuk setiap nilai variabel diskrit: x1, X2, X3,... Xyo, kejadian tertentu dari kejadian p (x = xyo). Fungsi ini juga dikenal sebagai "Fungsi Massa Probabilitas".
Distribusi probabilitas diskrit dapat diberikan dalam bentuk tabel atau grafik. Tabel memiliki bentuk umum ini, di mana variabel muncul dalam satu kolom dan probabilitas masing -masing di yang lain:
Fungsi massa probabilitas berbagi karakteristik umum berikut:
- Probabilitas pyo dari acara x apa punyo Ini antara 0 dan 1, bahkan beberapa dari nilai batas ini: 0 ≤ x ≤ 1.
- P (x = xyo) = pyo Oleh karena itu, ambil saja nilai positif: p (x = xyo) ≥ 0.
- Memang benar bahwa ∑ p (xyo) = 1 untuk semua nilai x yang mungkin.
Distribusi probabilitas menggambarkan perilaku populasi, yang dijelaskan oleh parameternya: rata -rata μ, varians σ2 dan standar deviasi s = σ σ2.
Selanjutnya, distribusi diskrit yang paling terkenal dijelaskan secara singkat:
Distribusi seragam
Itu adalah distribusi yang paling sederhana dari semuanya. Di dalamnya variabel dapat mengambil nilai diskrit "n": x1, X2, X3,... Xyo, Semua dengan kemungkinan yang sama. Dalam hal ini, distribusi diberikan oleh:
Distribusi binomial
Ini berlaku untuk pengalaman dengan hanya dua hasil yang mungkin dan saling eksklusif, yang biasanya disebut "keberhasilan" dan "kegagalan", masing -masing dilambangkan sebagai E dan F. Fakta bahwa suatu peristiwa disebut "kesuksesan," tidak selalu berarti bahwa itu adalah hal yang baik, itu lebih merupakan penunjukan yang sewenang -wenang.
Probabilitas keberhasilan p (e) dalam latihan "n", dilambangkan sebagai p, dan kegagalan p (f) seperti q = 1 - p.
Jika "X" mewakili sejumlah keberhasilan dalam uji coba independen "n", memang benar bahwa: 0 ≤ x ≤ n. Dan probabilitas kejadian p (x) dari peristiwa ini dihitung melalui rumus berikut:
Itu dapat melayani Anda: sentimeter persegi ke meter persegi (cm² ke m²)Di mana x = 0, 1, 2, 3 ..., n dan simbol (!) berarti "faktorial":
X! = x ∙ (x - 1) ∙ (x - 2) ∙ (x - 3)… 1
0! = 1
distribusi racun
Dalam distribusi ini, variabel acak x menunjukkan berapa kali peristiwa terjadi dalam beberapa interval, yang bisa dari waktu, jarak atau lainnya. Kejadian peristiwa itu acak, independen dan didistribusikan secara merata di seluruh interval yang dimaksud.
Setelah kondisi ini, probabilitas, yang tergantung pada rata -rata μ kejadian dan jumlah euler atau angka "e", dihitung oleh:
Kemungkinan peristiwa dengan distribusi ini kecil, jadi disebut "hukum kasus langka".
Pendekatan distribusi binomial
Distribusi Poisson berfungsi sebagai pendekatan untuk distribusi binomial ketika n besar (n≥ 100) dan p kecil (np ≤ 10). Dalam hal ini, rata -rata μ dihitung sebagai:
μ = n ∙ p
Distribusi hipergeometrik
Ini digunakan ketika probabilitas tidak independen, yaitu, setelah melakukan percobaan, kondisinya tidak sama lagi. Inilah yang terjadi saat mengekstraksi sampel tanpa penggantian dari suatu populasi, sehingga distribusi binomial tidak dapat lagi digunakan.
Jika populasi terdiri dari dua jenis objek yang berbeda dari dan B, dan pada objek acak dan tanpa penggantian, probabilitas mendapatkan objek x tipe A adalah:
Dimana a dan b adalah jumlah objek masing -masing dari masing -masing jenis, hadir dalam populasi.
Namun, jika populasinya sangat besar, bahkan jika tidak ada penggantian, sulit untuk elemen yang sama untuk dipilih lebih dari sekali, sehingga kedua distribusi: binomial dan hipergeometrik, menghasilkan hasil yang sama.
Dapat melayani Anda: Perbedaan kubus: Rumus, persamaan, contoh, latihanContoh
Koin diluncurkan
Co -launches adalah contoh yang sangat ilustratif:
-Peluncuran mata uang yang jujur, dan dapatkan wajah. Diketahui bahwa 1 wajah memiliki probabilitas ½ untuk pergi dan salib (0 wajah), sama. Distribusi ditampilkan dalam tabel ini:
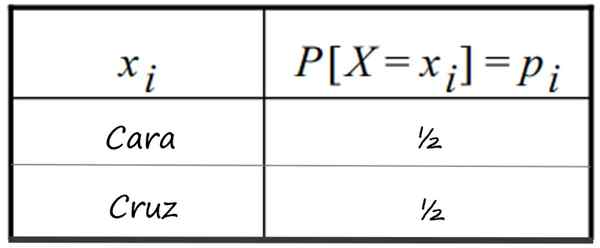 Tabel distribusi probabilitas diskrit yang mengikuti peluncuran 1 mata uang jujur. Sumber: f. Zapata
Tabel distribusi probabilitas diskrit yang mengikuti peluncuran 1 mata uang jujur. Sumber: f. Zapata -Tembakan simultan dua Koin jujur dan kemungkinan menghadap angka yang dapat diperoleh.
 Tabel distribusi probabilitas diskrit yang mengikuti peluncuran dua mata uang jujur, dengan maksud untuk mendapatkan wajah atau tidak. Sumber: f. Zapata
Tabel distribusi probabilitas diskrit yang mengikuti peluncuran dua mata uang jujur, dengan maksud untuk mendapatkan wajah atau tidak. Sumber: f. Zapata Variabel dengan distribusi yang seragam
-Pemilihan nomor integer yang bahkan atau ganjil: masing -masing probabilitas sama dengan ½ dari dipilih dalam himpunan bilangan bulat.
-Peluncuran dadu yang jujur. Dalam hal ini ada 6 wajah bernomor dan masing -masing memiliki probabilitas yang sama untuk pergi: 1/6.
-Pemilihan topik untuk mengikuti ujian, dipilih dari antara masalah N, jika semuanya sama -sama mungkin.
Variabel dengan distribusi binomial
-Jumlah wajah yang keluar dengan meluncurkan koin yang jujur.
-Dari populasi 250 keluarga, jumlahnya yang memiliki 2 anak.
-Jumlah rosewood yang bertahan, setelah seorang tukang kebun 20 rosales di sebuah taman.
-Dari sebuah penelitian dengan 50 pasien, jumlah mereka yang menunjukkan reaksi negatif terhadap suatu obat.
-Jumlah siswa yang disetujui dalam ujian probabilitas, dari kelompok yang terdiri dari 100 siswa.
Variabel dengan distribusi Poisson
-Jumlah panggilan per menit Pusat panggilan Dari sebuah perusahaan.
-Jumlah gempa besar per tahun untuk wilayah geografis tertentu.
-Jumlah tornado yang mempengaruhi wilayah tertentu selama setahun terakhir.
-Jumlah pohon yang terinfeksi jamur, per hektar hutan persegi.
Variabel dengan distribusi hipergeometrik
-Keberhasilan angka atau kombinasi pemenang dalam perjudian.
Dapat melayani Anda: vektor bersamaan: karakteristik, contoh dan latihan-Pemilihan sejumlah betina atau jantan dalam sampel ikan n dari fishbowl.
Latihan terpecahkan
Latihan 1
Sebuah studi menentukan bahwa dengan orang dewasa yang dipilih secara acak yang memiliki smartphone, 54% dari mereka menggunakannya di kelas atau rapat. Anda ingin menemukan probabilitas bahwa, secara acak memilih 8 orang dengan smartphone, tepatnya 6 dari mereka menggunakannya di kelas atau pertemuan.
Larutan
Eksperimen ini setuju dengan percobaan binomial, karena hasilnya adalah biner: seseorang mengambil telepon di kelas atau tidak mengeluarkannya. Fakta bahwa orang tersebut menggunakan ponsel yang berada di kelas dapat disebut sukses, dan gagal jika tidak (sebelum dijelaskan bahwa pilihan ini sepenuhnya sewenang -wenang).
Dalam hal ini: p = 0.54 dan q = 1- 0.54 = 0.46.
Karena 8 orang dipilih secara acak, maka n = 8 dan nilai x adalah 6, oleh karena itu, nilai yang diperlukan tersedia untuk menggantikannya dalam rumus distribusi binomial:
Latihan 2
Untuk tahun terakhir, sebuah klinik mendaftarkan 4221 kelahiran. Dengan data unik ini, tentukan probabilitas bahwa ada 15 kelahiran dalam 1 hari. Apakah acara ini jarang?
Larutan
Distribusi Poisson digunakan, karena diminta untuk menentukan probabilitas terjadinya suatu peristiwa yang terjadi dalam interval waktu. Dalam hal ini, variabelnya adalah jumlah kelahiran dan intervalnya adalah 1 hari.
Formula distribusi Poisson membutuhkan kelahiran rata -rata per hari, yang mudah dihitung:
Oleh karena itu, probabilitas x = 15 kelahiran/hari adalah:
Hasilnya dapat dinyatakan dalam persentase untuk kejelasan: 6.42% kemungkinan itu, pada hari apa pun, tepatnya 15 kelahiran terjadi. Acara ini tidak mungkin, meskipun tidak mungkin.


=\frac1n)
=\fracn!\left&space;(&space;n-x&space;\right&space;)!\cdot&space;x!\cdot\:p^x\cdot&space;q^n-x)
=\frac\mu&space;^x\cdot&space;e^-\mu&space;x!)
=\fracA!\left&space;(A-x&space;\right&space;)!\cdot&space;x!\cdot&space;\fracB!\left&space;(B-n+x&space;\right&space;)!\cdot&space;\left&space;(n-x&space;\right&space;)!\div&space;\frac\left&space;(A+B&space;\right&space;)!\left&space;(A+B-n&space;\right&space;)!\cdot&space;n!)
=\frac8!\left&space;(8-6&space;\right&space;)!\times&space;6!\times&space;0.54^6\times&space;0.46^\left&space;(8-6&space;\right&space;)=\frac8!2!\times&space;6!\times&space;0.54^6\times&space;0.46^2=0.147)

=\frac11.56^15\times&space;e^-11.5615!=0.0642)