Domain dan kontradominasi suatu fungsi (dengan contoh)

Konsep domain dan kontradiksi suatu fungsi Mereka umumnya diajarkan dalam kursus perhitungan yang diajarkan pada awal karir universitas.

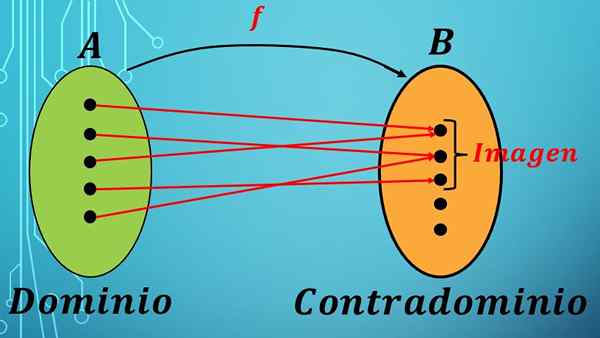
Sebelum mendefinisikan domain dan kontradiksi, Anda harus tahu apa fungsi itu. Fungsi F adalah hukum korespondensi (aturan) antara elemen dua set.

Seluruh elemen yang dipilih disebut domain fungsi, dan himpunan unsur -unsur ini dikirim melalui f disebut kontradominasi.

Dalam matematika fungsi dengan domain A dan kontradominasi B dilambangkan dengan ekspresi f: a → b.

Ekspresi sebelumnya mengatakan bahwa unsur -unsur set A dikirim ke set B mengikuti undang -undang korespondensi f.

Fungsi menetapkan setiap elemen dari set ke satu elemen set b b.

Domain dan kontradiksi

Mengingat fungsi nyata dari variabel nyata f (x), domain fungsi harus semua bilangan real sedemikian rupa sehingga, ketika dievaluasi dalam f, hasilnya adalah bilangan real.

Secara umum, kontradiksi suatu fungsi adalah himpunan angka N nyata. Kontradiksi juga disebut kedatangan atau kodominium set fungsi F.

Kontradiksi suatu fungsi selalu r?

TIDAK. Selama fungsinya tidak dipelajari secara rinci, set angka N nyata biasanya diambil sebagai kontradiksi.

Tetapi setelah fungsi dipelajari, set yang lebih tepat dapat diambil sebagai kontradominium, yang akan menjadi subset dari r.

Set yang sesuai yang disebutkan dalam paragraf sebelumnya bertepatan dengan gambar fungsi.

Definisi gambar atau rentang fungsi F mengacu pada semua nilai yang berasal dari mengevaluasi elemen domain di f.

Contoh domain dan kontradiksi

Dalam contoh -contoh berikut, cara menghitung domain fungsi dan gambarnya diilustrasikan.

Contoh 1

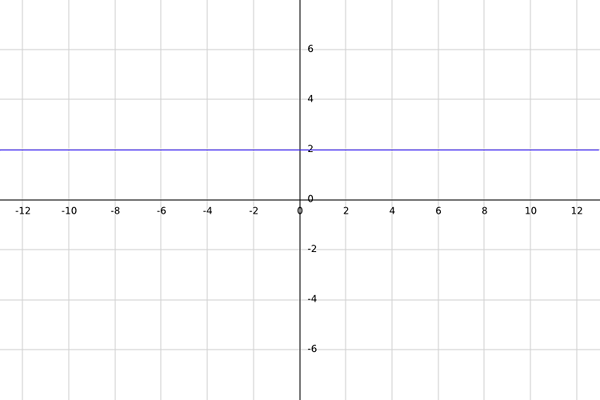
Biarkan f menjadi fungsi nyata yang ditentukan oleh f (x) = 2.

M -domain dari f adalah semua bilangan real sedemikian rupa sehingga, ketika mengevaluasinya di f, hasilnya adalah bilangan real. Kontradiksi untuk saat ini sama dengan R.

Karena fungsi yang diberikan konstan (selalu sama dengan 2), ia harus tidak peduli berapa pun bilangan real yang dipilih, karena ketika mengevaluasinya dalam hasilnya akan selalu sama dengan 2, yang merupakan bilangan real.

Oleh karena itu, domain fungsi yang diberikan adalah semua bilangan real; yaitu, a = r.

Sekarang sudah diketahui bahwa hasil fungsi selalu sama dengan 2, gambar fungsi hanya nomor 2, oleh karena itu kontradiksi fungsi dapat didefinisikan ulang sebagai b = img (f) = 2.

Oleh karena itu, f: r → 2.

Contoh 2

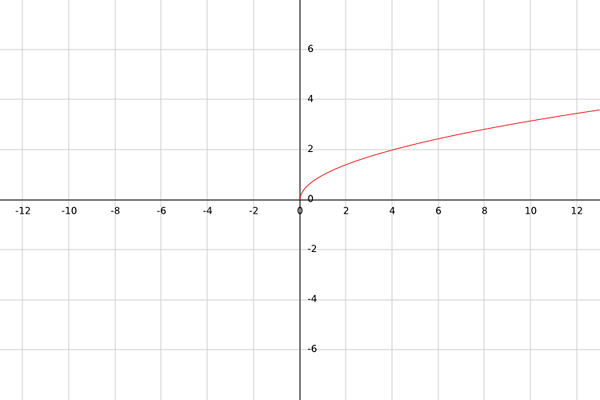
Misalkan G menjadi fungsi nyata yang ditentukan oleh g (x) = √x.

Selama gambar G tidak diketahui, kontradominium G adalah b = r.

Dengan fungsi ini harus diperhitungkan bahwa akar kuadrat hanya didefinisikan untuk angka non -negatif; yaitu angka yang lebih besar dari atau sama dari nol. Misalnya, √-1 bukan bilangan real.

Oleh karena itu, penguasaan fungsi G harus semua angka lebih besar dari atau sama dari nol; yaitu, x ≥ 0.

Oleh karena itu, a = [0,+∞).

Untuk menghitung kisaran, harus dicatat bahwa hasil g (x), karena itu adalah akar kuadrat, akan selalu lebih besar dari atau sama dengan. Yaitu, b = [0,+∞).

Kesimpulannya, g: [0,+∞) → [0,+∞).

Contoh 3

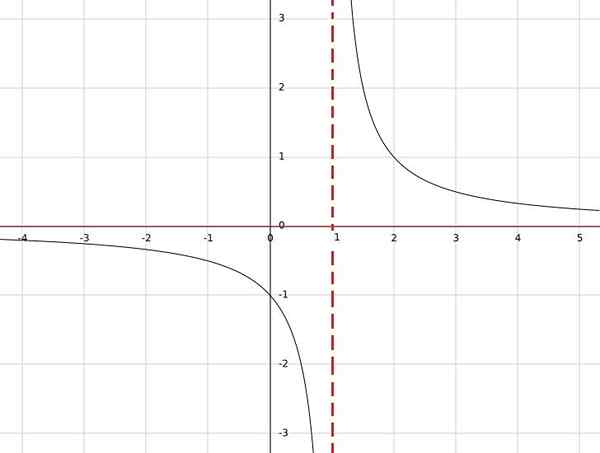
Jika Anda memiliki fungsi h (x) = 1/(x-1), fungsi ini tidak didefinisikan untuk x = 1, karena dalam penyebutnya akan diperoleh nol dan pembagian dengan nol tidak ditentukan.

Di sisi lain, untuk nilai riil lainnya hasilnya akan menjadi bilangan real. Oleh karena itu, domain semuanya reais kecuali satu; yaitu, a = r \ 1.

Dengan cara yang sama dapat dilihat bahwa satu -satunya nilai yang tidak dapat diperoleh sebagai hasilnya adalah 0, karena untuk sebagian kecil sama dengan nol pembilang harus nol.

Oleh karena itu, gambar fungsi adalah himpunan semua reais kecuali nol, maka diambil sebagai kontradominasi b = r 0.

Sebagai kesimpulan, h: r \ 1 → r \ 0.

Pengamatan

Domain dan gambar tidak harus menjadi set yang sama, seperti yang ditunjukkan dalam Contoh 1 dan 3.

Ketika suatu fungsi adalah grafik pada bidang Cartesian, domain diwakili oleh sumbu X dan kontradominium atau kisaran diwakili oleh sumbu y.