Persamaan umum garis yang kemiringannya sama dengan 2/3

Persamaan umum dari garis L adalah sebagai berikut: AX+oleh+C = 0, di mana a, b dan c konstan, x adalah variabel independen dan variabel dependen.

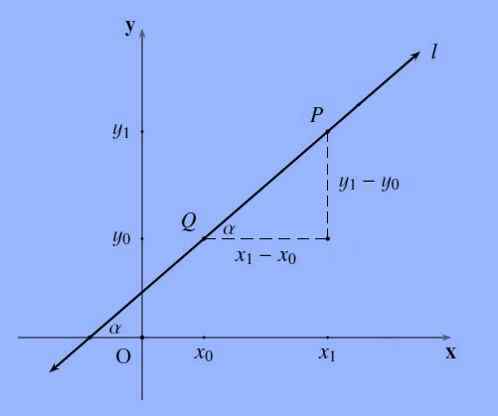
Kemiringan garis, dilambangkan secara umum dengan huruf M, yang melewati titik p = (x1, y1) dan q = (x0, y0) adalah hasil bagi berikut m: = (y1-y0)/(x1 -X0).

Kemiringan garis lurus mewakili kecenderungan; Mengatakan lebih formal, kemiringan garis adalah garis singgung sudut yang bentuknya dengan sumbu x.

Perlu dicatat bahwa urutan di mana titik-titik dinamai acuh tak acuh, karena (y0-y1)/(x0-x1) =-(y1-y0)/(-(x1-x0)) = (y1-y0) /(X1-x0).

Garis yang tertunda

Jika dua titik diketahui melaluinya garis lewat, mudah untuk menghitung kemiringannya. Tapi apa yang terjadi jika poin -poin ini tidak diketahui?

Mengingat persamaan umum ax+by+c = 0 baris, itu harus.

Apa persamaan umum garis yang kemiringannya 2/3?

Karena kemiringan garis adalah 2/3 maka kesetaraan ditetapkan -a/b = 2/3, yang dapat melihat bahwa a = -2 dan b = 3. Sehingga persamaan umum garis dengan kemiringan sama dengan 2/3 adalah -2x+3y+c = 0.

Harus diklarifikasi bahwa jika Anda dipilih a = 2 dan b = -3, persamaan yang sama akan diperoleh. Memang, 2x -3y+C = 0, yang sama dengan yang sebelumnya dikalikan dengan -1. Tanda C tidak masalah, karena itu adalah konstanta umum.

Pengamatan lain yang dapat dilakukan adalah bahwa untuk a = -4 dan b = 6 garis yang sama diperoleh, meskipun persamaan umumnya berbeda. Dalam hal ini persamaan umum adalah -4x+6y+c = 0.

Apakah ada cara lain untuk menemukan persamaan umum garis?

Jawabannya iya. Jika kemiringan garis diketahui ada dua bentuk, tambahan untuk yang sebelumnya, untuk menemukan persamaan umum.

Untuk ini, persamaan titik-pending dan persamaan pemotongan digunakan.

-Persamaan titik-pending: Jika m adalah kemiringan garis dan p = (x0, y0) titik di mana ia lewat, maka persamaan y-y0 = m (x-x0) disebut persamaan titik-pending titik.

-Persamaan pemotongan-pending: jika m adalah kemiringan garis dan (0, b) adalah potongan garis dengan sumbu y, maka persamaan y = mx+b disebut persamaan pemotongan-pending.

Menggunakan kasus pertama, diperoleh bahwa persamaan titik yang ditunda dari suatu garis yang kemiringannya 2/3 diberikan oleh ekspresi y-y0 = (2/3) (x-x0).

Untuk mencapai persamaan umum, semua istilah dikalikan dengan 3 di kedua sisi dan dikelompokkan bersama, dengan demikian mendapatkan -2x+3y+(2 × 0-3y0) = 0 adalah persamaan umum garis, di mana c = 2 × 0-3Y0.

Jika kasus kedua digunakan, diperoleh bahwa persamaan garis yang sedang dipotong dari suatu garis yang kemiringannya 2/3 adalah y = (2/3) x+b.

Sekali lagi, mengalikan 3 di kedua sisi, dan mengelompokkan semua variabel, diperoleh -2x+3y -3b = 0. Yang terakhir adalah persamaan umum dari garis di mana c = -3b.

Sebenarnya, melihat erat pada kedua kasus, dapat dilihat bahwa kasus kedua hanyalah kasus tertentu dari yang pertama (ketika x0 = 0).