Formula persamaan kelas satu, cara menyelesaikannya, contoh, latihan

Itu Tingkat Pertama atau Persamaan Linear Dengan yang tidak diketahui adalah mereka yang dapat dinyatakan sebagai jumlah dari dua istilah, dengan cara berikut:

kapak + b = 0

Di mana A dan B, dengan ke ≠ 0, adalah bilangan real r atau juga kompleks c. Untuk menyelesaikannya, istilah dialihkan, yang berarti mengubah istilah dari satu sisi ke kesetaraan lain.

Gambar 1. Persamaan linier adalah y = mx + c bentuk dengan y = 0. Sumber: Pxhere.

Untuk menghapus yang tidak diketahui, istilah +B dialihkan, yang harus pergi ke sisi kanan kesetaraan dengan tanda yang diubah.

AX = -B

Kemudian nilai x dibersihkan, dengan cara ini:

x = - b/a

Sebagai contoh, kami akan menyelesaikan persamaan berikut:

6x - 5 = 4

Kami mengubah istilah -5 ke sisi kanan dengan tanda yang diubah:

6x = 4 + 5

Ini setara dengan menambahkan 5 di kedua sisi persamaan asli:

6x - 5 + 5 = 4 + 5 → 6x = 9

Dan sekarang kita menghapus "X" yang tidak diketahui:

x = 9/6 = 3/2

Yang setara dengan membagi kedua sisi kesetaraan dengan 6. Jadi kita dapat menilai yang berikut untuk mendapatkan solusi:

-Jumlah yang sama dapat ditambahkan atau dikurangi kedua sisi kesetaraan dalam suatu persamaan, tanpa mengubahnya.

-Anda juga dapat mengalikan (atau membagi) dengan jumlah yang sama dengan semua istilah baik di sebelah kiri maupun di sebelah kanan persamaan.

-Dan jika kedua anggota persamaan meningkat dengan kekuatan yang sama, kesetaraan juga tidak diubah.

[TOC]

Cara menyelesaikan persamaan tingkat pertama

Solusi dari persamaan tingkat pertama juga dikenal sebagai akar yang sama. Itu adalah nilai x yang mengubah ekspresi asli menjadi kesetaraan. Misalnya di:

5x = 8x - 15

Jika kita mengganti x = 5 dalam persamaan ini, diperoleh:

5⋅5 = 8⋅5 - 15

25 = 40 - 15

25 = 25

Ketika persamaan linear tingkat pertama datang dalam banyak hal, yang kadang -kadang tidak jelas, ada serangkaian aturan umum yang terdiri dari beberapa manipulasi aljabar, untuk menemukan nilai yang tidak diketahui:

-Pertama, jika ada operasi yang ditunjukkan, ini harus dilakukan.

-Simbol pengelompokan seperti tanda kurung, kurung persegi dan kunci, jika ada, harus ditekan dengan mempertahankan tanda -tanda yang sesuai.

-Istilah -istilah tersebut ditransfer untuk menempatkan semua yang mengandung tidak diketahui ke satu sisi kesetaraan, dan yang tidak mengandungnya ke yang lain.

-Maka semua istilah serupa dikurangi, untuk mencapai formulir AX = -B.

-Dan langkah terakhir adalah menghapus yang tidak diketahui.

Interpretasi grafis

Persamaan tingkat pertama yang diangkat pada awalnya dapat diturunkan dari persamaan garis y = mx+c, melakukan y = 0. Nilai x yang hasilnya sesuai dengan persimpangan garis dengan sumbu horizontal.

Dalam gambar berikut Anda memiliki tiga baris. Dimulai dengan garis hijau, yang persamaannya adalah:

Dapat melayani Anda: faktorisasi

y = 2x - 6

Membuat y = 0 di baris garis persamaan tingkat pertama diperoleh:

2x - 6 = 0

Solusinya adalah x = 6/2 = 3. Sekarang ketika kami merinci grafik, mudah untuk disadari bahwa pada dasarnya, garis memotong ke sumbu horizontal pada x = 3.

Garis biru memotong sumbu x pada x = 5, yang merupakan solusi untuk persamaan -x + 5 = 0. Akhirnya, garis yang persamaannya adalah y = 0.5x + 2 potong ke sumbu x pada x = -4, yang mudah diperingatkan tentang persamaan tingkat pertama:

0.5 x + 2 = 0

x = 2/0.5 = 4

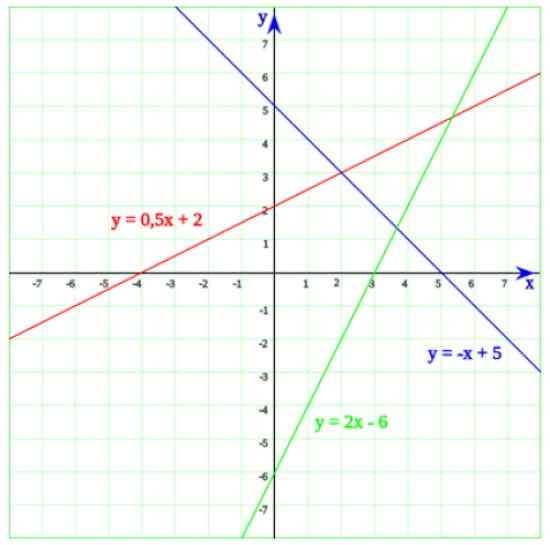Gambar 2. Tiga baris yang persimpangannya dengan sumbu horizontal sesuai dengan persamaan linier. Sumber: Wikimedia Commons.

Contoh persamaan linier sederhana   

Seluruh persamaan

Mereka adalah mereka yang tidak ada penyebut, misalnya:

21 - 6x = 27 - 8x

Solusinya adalah:

-6x + 8x = 27 - 21

2x = 6

x = 3

Persamaan pecahan

Persamaan ini mengandung setidaknya satu penyebut yang berbeda dari 1. Untuk menyelesaikannya, itu disarankan.

Persamaan berikut adalah tipe fraksional:

Denominator adalah 6, 8 dan 12 dan kelipatan umum minimumnya, dilambangkan sebagai m.C.M (6, 8,12) adalah sedikit pun dari angka yang berisi penyebut ini.

Karena angka -angka ini kecil, tidak sulit untuk melihat bahwa m.C.M (6, 8,12) = 24. Hasil ini mudah diperoleh dengan mengekspresikan angka sebagai produk bilangan prima atau kekuatannya, mari kita lihat:

6 = 3.2

8 = 2³

12 = 2²⋅3

Kelipatan umum minimum ditentukan dengan mengalikan faktor umum dan non -umum dari 6, 8 dan 12 dengan eksponen terbesar, lalu:

MCM (6,8,12) = 2³ ⋅3 = 8 × 3 = 24

Karena kelipatan umum minimum tersedia, ia harus dikalikan dengan masing -masing ketentuan persamaan:

Dengan cara ini para penyebut ditekan dan ada persamaan dengan produk, lebih mudah dipecahkan:

4 (x+5) -3 (2x+3) = 2 (1-5x)

Kami menggunakan properti distributif:

4x + 20 - 6x -9 = 2 - 10x

Semua istilah yang mengandung "X" yang tidak diketahui dikelompokkan ke sisi kiri kesetaraan, meninggalkan istilah independen atau numerik dari sisi kanan:

4x - 6x + 10 x = 2 +9 - 20

8x = -9

x = - 9/8

Persamaan literal

Mereka adalah persamaan linier dengan yang tidak diketahui, yang bagaimanapun disertai dengan koefisien literal (huruf). Surat -surat ini diperlakukan seperti yang akan dilakukan dengan angka. Contoh persamaan literal pertama adalah:

-3ax + 2a = 5x - b

Persamaan ini diselesaikan dengan cara yang sama seperti jika istilah dan koefisien independen adalah numerik:

-3ax - 5x = - b - 2a

Faktoring "X" yang tidak diketahui:

x (-3a - 5) = - b - 2a

x = ( - b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)

Sistem Persamaan Tingkat Pertama 

Sistem persamaan terdiri dari serangkaian persamaan dengan dua atau lebih tidak diketahui. Solusi sistem terdiri dari nilai -nilai yang memenuhi persamaan secara bersamaan dan untuk menentukannya secara tegas, harus ada persamaan untuk setiap yang tidak diketahui.

Dapat melayani Anda: aljabar vektor

Bentuk umum dari suatu sistem M Persamaan linier dengan N Tidak diketahui adalah:

ke_sebelasX₁ + ke₁₂X₂ +… ke_1nX_N = b₁
ke_{dua puluh satu}X₁ + ke₂₂X₂ +… ke_2nX_N = b₂
..
ke_M1X₁ + ke_M2X₂ +… ke_{M N}X_N = b_M

Jika sistem memiliki solusi, dikatakan demikian ditentukan kompatibel, Ketika ada serangkaian nilai tak terbatas yang memuaskannya kompatibel tidak ditentukan, Dan akhirnya, jika tidak memiliki solusi, maka itu tidak sesuai.

Dalam resolusi sistem persamaan linier beberapa metode digunakan: reduksi, penggantian, pemerataan, metode grafis, eliminasi Gauss-Jordan dan penggunaan penentu adalah di antara yang paling banyak digunakan. Tetapi ada algoritma lain untuk mencapai solusi, lebih nyaman untuk sistem dengan banyak persamaan dan tidak diketahui.

Contoh sistem persamaan linier dengan dua yang tidak diketahui adalah:

8x - 5 = 7y - 9
6x = 3y + 6

Solusi dari sistem ini diajukan nanti di bagian Latihan yang Dipecahkan.

Persamaan linier dengan nilai absolut

Nilai absolut dari bilangan real adalah jarak antara lokasinya pada garis angka dan 0 yang sama. Menjadi jarak nilainya selalu positif.

Nilai absolut dari suatu angka dilambangkan dengan bilah modul: │x│. Nilai absolut dari angka positif atau negatif selalu positif, misalnya:

│+8│ = 8

│-3│ = 3

Dalam persamaan dengan nilai absolut, yang tidak diketahui adalah antara bilah modul. Pertimbangkan persamaan sederhana berikut:

│X│ = 10

Ada dua kemungkinan, yang pertama adalah bahwa X adalah angka positif, dalam hal ini kita miliki:

x = 10

Dan kemungkinan lainnya adalah bahwa X adalah angka negatif, dalam hal ini:

x = -10

Ini adalah solusi dari persamaan ini. Sekarang mari kita lihat contoh yang berbeda:

│x+6│ = 11

Jumlah di dalam batang bisa positif, lalu:

x+6 = 11

x = 11 -6 = 5

Atau bisa negatif. Dalam hal itu:

-(x+6) = 11

-x - 6 = 11 ⇒ -x = 11+6 = 17

Dan nilai yang tidak diketahui adalah:

x = -17

Persamaan nilai absolut ini karenanya memiliki dua solusi: x₁ = 5 dan x₂ = -17. Kami dapat memverifikasi bahwa kedua solusi mengarah pada kesetaraan dalam persamaan asli:

│5+6│ = 11

│11│ = 11

DAN

│-17+6│ = 11

│-11│ = 11

Latihan terpecahkan sederhana

- Latihan 1

Selesaikan sistem persamaan linier berikut dengan dua tidak diketahui:

8x - 5 = 7y -9
6x = 3y + 6

Larutan

Saat sistem ini dinaikkan, ini cocok untuk menggunakan metode penggantian, karena dalam persamaan kedua yang tidak diketahui X Hampir siap untuk izin:

x = (3y + 6)/6

Dapat melayani Anda: aljabar

Dan Anda dapat segera mengganti persamaan pertama, yang kemudian menjadi persamaan -legree pertama dengan tidak diketahui "y":

8 [(3y + 6)/6] - 5 = 7y - 9

Denominator dapat ditekan jika setiap istilah dikalikan dengan 6:

6 . 8⋅ [(3y + 6)/6] - 6.5 = 6 .7y- 6 . 9

8⋅ (3y + 6) - 30 = 42y - 54

Menerapkan properti distributif dalam jangka waktu pertama di sebelah kanan kesetaraan:

24y + 48 -30 = 42y - 54 ⇒ 24y + 18 = 42y - 54

Persamaan dapat disederhanakan, karena semua koefisien adalah kelipatan 6:

4y + 3 = 7y - 9

-3y = -12

y = 4

Dengan hasil ini kita pergi ke izin x:

x = (3y +6)/6 → x = (12 +6)/6 = 3

- Latihan 2

Selesaikan persamaan berikut:

Larutan

Dalam persamaan ini, produk muncul, dan mengikuti instruksi yang diberikan di awal, mereka harus dikembangkan terlebih dahulu:

3x - 10x +14 = 5x + 36x + 12

Maka semua istilah yang mengandung tidak diketahui dibawa ke sisi kiri kesetaraan, dan di sisi kanan persyaratan independen adalah:

3x - 10x - 5x - 36x = 12 - 14

-48x = -2

x = 1/24

- Latihan 3

Dengan menambahkan tiga sudut interior segitiga, 180º diperoleh. Yang terbesar melebihi anak dalam 35º, dan ini pada gilirannya melebihi 20º perbedaan antara yang terbesar dan menengah. Apa sudutnya?

Larutan

Kami akan memanggil "x" ke sudut utama, "y" ke media dan "z" untuk anak. Ketika pernyataan tersebut menyatakan bahwa jumlahnya adalah 180º Anda dapat menulis:

x + y + z = 180

Kemudian kita tahu bahwa yang tertua melebihi anak dalam 35º, kita dapat menulis ini:

X = z + 35

Akhirnya, anak melebihi 20 º ke perbedaan antara yang terbesar dan sedang:

Z = x - y + 20

Kami memiliki sistem 3 persamaan dan 3 tidak diketahui:

x + y + z = 180

X = z + 35

Z = x - y + 20

Dengan membersihkan persamaan pertama, Anda memiliki:

Z = 180 - x - y

Mencocokkan yang ketiga:

180 - x - y = x - y + 20

Melewati yang tidak diketahui ke sisi kiri seperti biasa:

-x - y - x + y = 20 - 180

"Y" dibatalkan dan tetap:

-2x = - 160

x = 80º

Persamaan kedua adalah nilai z:

Z = x - 35 = 80 - 35 = 45º

Dan nilai dan dari yang pertama atau ketiga:

y = 180 - x - z = 180 - 80 - 45 = 55º

Referensi

1. Baldor. 1977. Aljabar Dasar. Edisi Budaya Venezuela.
2. Institut Monterey. Persamaan, ketidaksetaraan dan nilai absolut. Pulih dari: montereyinstitute.org.
3. Guru online. Klasifikasi persamaan linier atau tingkat pertama. Pulih dari: profesor inline.Cl.
4. Hoffman, J. Pemilihan masalah matematika. Volume 2.
5. Jiménez, r. 2008. Aljabar. Prentice Hall.
6. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.