Formula Persamaan Tingkat Kedua, Cara menyelesaikannya, Contoh, Latihan
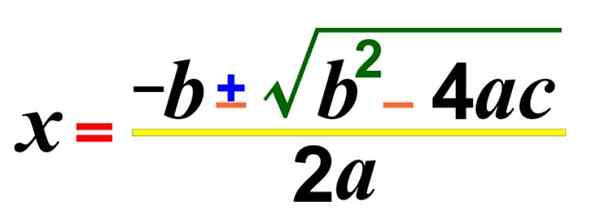
- 2424
- 461
- Ray Thiel
Itu Persamaan tingkat kedua atau kuadratik Dan yang tidak diketahui memiliki formulir kapak2 + bx + c = 0. Di mana A ≠ 0, karena menjadi 0, persamaan akan diubah menjadi persamaan linier, dan koefisien A, B dan C adalah bilangan real.
Yang tidak diketahui ditentukan adalah nilai x. Misalnya, persamaan 3x2 - 5x + 2 = 0 adalah persamaan tingkat kedua yang lengkap.
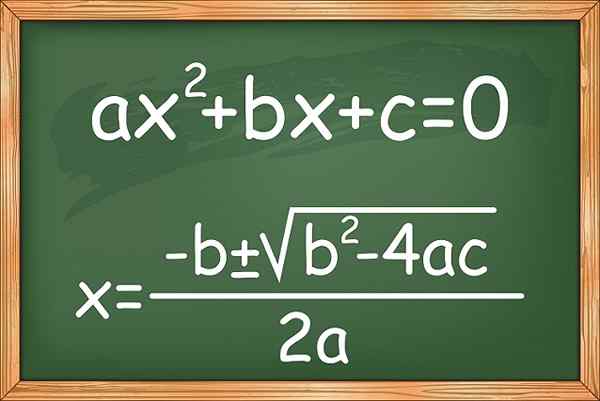 Gambar 1. Rumus untuk memecahkan persamaan tingkat kedua atau kuadratik dari yang tidak diketahui
Gambar 1. Rumus untuk memecahkan persamaan tingkat kedua atau kuadratik dari yang tidak diketahui Ada juga varian yang dikenal sebagai persamaan bagian kedua yang tidak lengkap, yang tidak memiliki ketentuan, kecuali dari kapak2. Berikut beberapa contoh:
X2 - 25 = 0
3x2 - 5x = 0
Al Juarisme, matematikawan kuno Arab yang terkenal, dijelaskan dalam karya -karyanya berbagai jenis persamaan tingkat pertama dan kedua, tetapi hanya dengan koefisien positif. Namun, itu adalah matematika Prancis Obat anti radang:
Ini adalah formula umum yang memungkinkan untuk memecahkan persamaan kuadratik, menemukan akar atau nol yang sama, bahkan jika solusinya tidak nyata. Ada juga cara lain untuk menyelesaikannya.
[TOC]
Cara menyelesaikan persamaan kelas dua?
Persamaan -Degree kedua dapat diselesaikan dengan rumus yang diberikan di atas, dan ada juga prosedur aljabar lain yang dapat bekerja dalam beberapa persamaan.
Kami akan menyelesaikan persamaan yang diusulkan di awal dengan rumus, metode yang valid untuk persamaan tingkat kedua dengan yang tidak diketahui:
3x2 - 5x + 2 = 0
Untuk menggunakan rumus, kami mencatat dengan benar bahwa:
- ke Itu adalah koefisien istilah dengan x2
- B Itu adalah koefisien istilah linier
- C adalah istilah independen.
Mari kita identifikasi mereka dari persamaan yang sama:
A = 3
B = -5
C = 2
Perhatikan bahwa tanda yang menyertai koefisien harus diperhitungkan. Sekarang kami mengganti nilai -nilai ini dalam rumus:
Dalam pembilang adalah simbol "lebih banyak - lebih sedikit" ±, yang menunjukkan bahwa kuantitas dengan akar dapat dianggap positif dan juga negatif. Persamaan tingkat kedua memiliki maksimal dua solusi nyata, dan simbol ini memperhitungkannya.
Mari Hubungi X1 dan x2 Untuk dua solusi ini, lalu:
X1 = (5+1) / 6 = 1
X2 = (5-1)/6 = 4/6 = 2/3
Resolusi dengan faktorisasi
Beberapa persamaan tingkat kedua terdiri dari trinomial yang mudah menjadi faktor. Jika demikian, metode ini jauh lebih cepat. Pertimbangkan persamaannya:
X2 + 7x - 18 = 0
Faktorisasi memiliki bentuk ini:
Dapat melayani Anda: kongruensi: angka kongruen, kriteria, contoh, latihan(x +) ⋅ (x -)
Ruang kosong diisi dengan dua angka yang, ketika dikalikan dengan 18, dan ketika dikurangi, 7 adalah 7. Tanda -tanda dalam tanda kurung dipilih dengan kriteria ini:
-Dalam tanda kurung pertama, tanda antara istilah pertama dan kedua ditempatkan.
-Dan dalam tanda kurung kedua menjadi produk dari tanda -tanda yang terlihat.
Adapun angka, mereka mudah dalam hal ini: mereka 9 dan 2. Yang tertua selalu ditempatkan di tanda kurung pertama, seperti ini:
X2 + 7x - 18 = (x + 9). (x - 2)
Pembaca dapat memeriksa melalui properti distributif, yang saat mengembangkan produk dari sisi kanan kesetaraan, trinomial kiri diperoleh. Sekarang, persamaannya ditulis ulang:
(x + 9) ⋅ (x - 2) = 0
Agar kesetaraan terpenuhi, itu cukup untuk salah satu dari dua faktor menjadi nol. Jadi, yang pertama harus dilakukan1 = -9 atau mungkin faktor kedua dibatalkan, dalam hal ini x2 = 2. Ini adalah solusi persamaan.
Metode grafis
Akar atau solusi persamaan tingkat kedua sesuai dengan persimpangan perumpamaan y = = kapak2 + BX + C Dengan sumbu horizontal atau sumbu x. Sehingga dengan memberi grafik, perumpamaan yang sesuai kita akan menemukan solusi dari persamaan tingkat kedua melakukan y = 0.
Pemotongan perumpamaan dengan sumbu horizontal mewakili solusi dari persamaan kapak2 + bx + c = 0. Perumpamaan yang hanya memotong sumbu horizontal pada satu titik memiliki akar tunggal dan ini akan selalu menjadi simpul parabola.
Dan akhirnya, jika perumpamaan tidak memotong ke sumbu horizontal, persamaan yang sesuai kapak2 + bx + c = 0 Itu tidak memiliki solusi nyata.
Membangun grafik tangan bisa melelahkan, tetapi dengan menggunakan program yang grafik itu sangat sederhana.
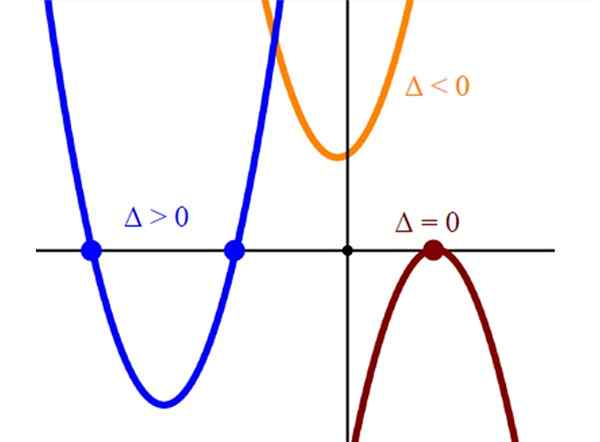 Gambar 2. Representasi grafis dari tiga jenis perumpamaan, dengan dua, satu dan tanpa persimpangan dengan sumbu horizontal. Sumber: Wikimedia Commons.
Gambar 2. Representasi grafis dari tiga jenis perumpamaan, dengan dua, satu dan tanpa persimpangan dengan sumbu horizontal. Sumber: Wikimedia Commons. Resolusi dengan kalkulator ilmiah
Banyak model kalkulator ilmiah memiliki opsi untuk memecahkan persamaan tingkat kedua (dan juga jenis persamaan lainnya). Untuk mengetahuinya, Anda harus meninjau menu.
Setelah opsi persamaan kuadratik yang tidak diketahui dipilih, menu meminta untuk memasukkan nilai koefisien A, B dan C dan mengembalikan solusi nyata jika ada. Dan ada juga model kalkulator ilmiah yang bekerja dengan bilangan kompleks dan menawarkan solusi ini.
Dapat melayani Anda: kelipatan 2: apa itu dan penjelasanDiskriminasi dari persamaan tingkat kedua
Untuk mengetahui apakah persamaan memiliki solusi nyata atau tidak, dan berapa banyak, tanpa perlu menyelesaikan terlebih dahulu, diskriminan didefinisikan sebagai jumlah di bawah akar kuadrat:
Δ = b2 - 4ac
Menurut tanda diskriminan, diketahui berapa banyak solusi yang dimiliki persamaan sesuai dengan kriteria ini:
-Dua solusi nyata: δ> 0
-Solusi nyata (atau dua solusi identik): Δ = 0
-Tidak ada solusi nyata: Δ < 0
Misalnya, berapa banyak solusi yang dimiliki persamaan tingkat kedua -7x2 +12x + 64 = 0? Kami mengidentifikasi koefisien:
A = -7
B = 12
C = 64
Δ = b2 - 4ac = 122 - 4x (-7) x 64 = 144 + 1792 = 1936> 0
Persamaan ini memiliki dua solusi. Sekarang mari kita lihat yang ini:
X2 - 6x + 9 = 0
A = 1
B = -6
C = 9
Δ = (-6)2 - 4 x 1 x 9 = 36 - 36 = 0
Ini adalah persamaan dengan solusi unik atau dua solusi yang sama.
Contoh persamaan tingkat kedua sederhana
Pada awalnya kami mengatakan bahwa persamaan tingkat kedua dapat diselesaikan jika trinomial, dan tidak lengkap jika istilah linier atau istilah independen hilang. Sekarang mari kita lihat beberapa jenis tertentu:
X Form Persamaan2 + mx + n = 0
Dalam hal ini a = 1 dan formula dikurangi menjadi:
Untuk jenis persamaan ini, dan selalu tergantung pada koefisien yang tersisa, metode faktorisasi dapat bekerja dengan baik, seperti yang kita lihat di bagian sebelumnya.
Persamaan bentuk kapak yang tidak lengkap2 + C = 0
Solusinya, jika ada, adalah bentuknya:
Ada solusi nyata ketika O C memiliki tanda negatif, tetapi jika kedua istilah tersebut memiliki tanda yang sama, solusinya akan menjadi imajiner.
Persamaan bentuk kapak yang tidak lengkap2 + Bx = 0
Persamaan ini dengan cepat diselesaikan dengan menggunakan faktorisasi, karena x adalah faktor umum dalam kedua istilah. Salah satu solusinya selalu x = 0, yang lain seperti ini:
kapak2 + Bx = 0
x (kapak + b) = 0
AX + B = 0 → X = -B/A
Mari kita lihat contoh kemudian. Menyelesaikan:
X2 - 5x = 0
x (x - 5) = 0
Oleh karena itu x1 = 0 dan x2 = 5
Persamaan dengan penyebut
Ada beberapa persamaan rasional, di mana yang tidak diketahui dapat hadir baik dalam pembilang maupun di denominator, atau bahkan hanya dalam yang terakhir, dan bahwa dengan manipulasi aljabar dikurangi menjadi persamaan kuadratik.
Cara untuk menyelesaikannya adalah dengan melipatgandakan kedua sisi kesetaraan dengan ganda umum minimum atau m.C.m dari penyebut dan kemudian mengatur ulang persyaratan. Misalnya:
Dapat melayani Anda: berapa banyak diameter yang dimiliki keliling?Persamaan orde tinggi yang diubah menjadi kuadratik
Ada persamaan urutan yang lebih tinggi yang, melalui perubahan variabel, dapat diselesaikan seolah -olah mereka kuadratik, misalnya persamaan ini Bicadrada:
X4 - 10x2 + 9 = 0
Biarkan x2 = U, maka persamaan diubah menjadi:
atau2 - 10U + 9 = 0
Persamaan ini dengan cepat diselesaikan dengan faktorisasi, menemukan dua angka yang dikalikan dalam 9 dan ditambahkan 10. Angka -angka ini adalah 9 dan 1:
(U - 9).(U - 1) = 0
Oleh karena itu solusi dari persamaan ini adalah u1 = 9 dan u2 = 1. Sekarang kita mengembalikan perubahan:
X2 = 9 → x1 = 3 dan x2 = -3
X2 = 1 → x1 = 1 dan x2 = -1
Persamaan asli adalah urutan 4, oleh karena itu memiliki setidaknya 4 akar. Contohnya adalah -3, -1, 1 dan 3.
Latihan terpecahkan sederhana
- Latihan 1
Selesaikan persamaan kuadratik berikut dengan yang tidak diketahui di denominator:
Kelipatan umum minimum adalah x (x+2) dan harus berlipat ganda dengan semua istilah:
Ekspresi yang setara tetap:
5x (x+2) - x = x (x+2)
Kami mengembangkan:
5x2 + 10x - x = x2 + 2x
Semua istilah dialihkan ke kiri kesetaraan dan ke kanan tertinggal 0:
5x2 + 10x - x - x2 - 2x = 0
4x2 - 7x = 0
We Factor, karena ini adalah persamaan yang tidak lengkap:
x (4x - 7) = 0
Salah satu solusinya adalah x = 0, yang lain adalah:
4x = 7
x = 7/4
- Latihan 2
Temukan solusi persamaan tingkat kedua:
a) -7x2 +12x + 64 = 0
b) x2 - 6x + 9 = 0
Solusi untuk
Dari persamaan ini kita tahu penentu Δ, karena dihitung sebagai contoh sebelumnya, jadi kita akan memanfaatkannya, mengekspresikan rumus pelarut sebagai berikut:
X1 = (-12+44)/ - 14 = - (32/14) = - (16/7)
X2 = (-12 -44) / -14 = 4
Solusi b
Trinomial kuadrat x2 - 6x + 9 dapat dilakukan, karena merupakan trinomial persegi yang sempurna:
X2 - 6x + 9 = (x-3)2 = 0
Solusi dari persamaan ini adalah x = 3.
- Latihan 3
Apa persamaan yang solusinya 3 dan 4?
Larutan
Ekspresi faktorisasi adalah:
(x - 3) ⋅ (x - 4) = 0
Menerapkan properti distributif:
X2 - 4x -3x + 12 = 0
Dua istilah pusat serupa dan dapat dikurangi, menjadi: Meninggalkan:
X2 - 7x + 12 = 0
Referensi
- Baldor. 1977. Aljabar Dasar. Edisi Budaya Venezuela.
- Hoffman, J. Pemilihan masalah matematika. Volume 2.
- Jiménez, r. 2008. Aljabar. Prentice Hall.
- Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
- Zapata, f. 4 cara untuk menyelesaikan persamaan tingkat kedua. Pulih dari: francesphysics.Blogspot.com.
- Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.
- « Struktur Polimer Penambahan, Karakteristik, Fungsi, Penggunaan
- Karakteristik dan contoh motivasi intrinsik »



\pm&space;\sqrt(-5)^2-4\times&space;3\times&space;22\times&space;3=)

^2-4c2)


x-\fracx(x+2)x+2=x(x+2))
=\frac-12\pm&space;44-14)