Persamaan polinomik

Apa persamaan polinomial?

Itu Persamaan polinomik Mereka adalah pernyataan yang meningkatkan kesetaraan dua ekspresi atau anggota, di mana setidaknya salah satu istilah yang membentuk setiap sisi kesetaraan adalah polinomial P (x). Persamaan ini dinamai sesuai dengan tingkat variabelnya.

Secara umum, persamaan adalah pernyataan yang menetapkan kesetaraan dua ekspresi, di mana setidaknya satu di antaranya ada jumlah yang tidak diketahui, yang disebut variabel atau tidak diketahui. Meskipun ada banyak jenis persamaan, ini umumnya diklasifikasikan ke dalam dua jenis: aljabar dan transenden.

Persamaan polinomik hanya mengandung ekspresi aljabar, yang dapat memiliki satu atau lebih tidak diketahui yang mengintervensi dalam persamaan. Menurut eksponen (kelas) yang mereka miliki, mereka dapat diklasifikasikan sebagai: kelas satu (linier), kelas dua (kuadratik), kelas tiga (kubik), kelas empat (quantic), derajat lebih dari atau sama dengan lima dan irasional.

Karakteristik persamaan polinomial

Persamaan polinomik adalah ekspresi yang dibentuk oleh kesetaraan antara dua polinomial; Yaitu, untuk jumlah terbatas dari perkalian antara nilai yang tidak diketahui (variabel) dan angka tetap (koefisien), di mana variabel dapat memiliki eksponen, dan nilainya dapat menjadi bilangan bulat positif, termasuk nol.

Eksponen menentukan tingkat atau jenis persamaan. Istilah ekspresi yang memiliki eksponen nilai paling banyak akan mewakili tingkat absolut polinomial.

Persamaan polinomik juga dikenal sebagai aljabar, koefisiennya dapat menjadi bilangan real atau kompleks dan variabel adalah angka yang tidak diketahui yang diwakili oleh surat, seperti: "x".

Jika dengan mengganti nilai dengan variabel "x" dalam p (x) hasilnya sama dengan nol (0), maka dikatakan bahwa nilai ini memenuhi persamaan (itu adalah solusi), dan umumnya disebut akar polinomial akar polinomial.

Ketika persamaan polinomial dikembangkan, semua akar atau solusi ingin ditemukan.

Jenis Persamaan Polinomial

Ada beberapa jenis persamaan polinomial, yang dibedakan sesuai dengan jumlah variabel, dan juga sesuai dengan tingkat eksponennya.

Dengan demikian, persamaan polinomial -di mana istilah pertamanya adalah polinomial yang hanya memiliki satu yang tidak diketahui, mengingat gelar dapat menjadi angka alami (n) dan istilah kedua adalah nol -dapat dinyatakan sebagai berikut:

Dapat melayani Anda: Sejarah Trigonometri dari Asalnya

ke_{N *} X^N + ke_{N-1 *} X^N-1 +... + a_{1 *} X¹ + ke_{0 *} X₀ = 0

Di mana:

• ke_N, ke_N-1 sudah₀, Mereka adalah koefisien nyata (angka).
• ke_N berbeda dari nol.
• Eksponen n adalah bilangan bulat positif yang mewakili tingkat persamaan.
• x adalah variabel atau tidak diketahui yang harus dicari.

Tingkat absolut atau lebih besar dari persamaan polinomial adalah bahwa eksponen nilai yang lebih besar di antara semua yang membentuk polinomial; Dengan cara ini, persamaan diklasifikasikan sebagai:

Kelas satu

Persamaan polinomial derajat pertama, juga dikenal sebagai persamaan linier, adalah yang di mana derajat (eksponen terbesar) sama dengan 1, polinomial adalah dari bentuk p (x) = 0; Dan itu terdiri dari istilah linier dan independen. Itu ditulis sebagai berikut:

kapak + b = 0.

Di mana:

• A dan B adalah bilangan real dan ≠ 0.
• Kapak adalah istilah linier.
• B adalah istilah independen.

Misalnya, Persamaan 13x - 18 = 4x.

Untuk menyelesaikan persamaan linier, semua istilah yang mengandung X yang tidak diketahui harus diteruskan ke sisi kesetaraan, dan yang tidak bergerak di sisi lain, untuk membersihkannya dan mendapatkan solusi:

13x - 18 = 4x

13x = 4x + 18

13x - 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

Dengan cara ini, persamaan yang diberikan hanya memiliki satu solusi atau root, yaitu x = 2.

Kelas dua

Persamaan polinomial derajat kedua, juga dikenal sebagai persamaan kuadratik, adalah yang di mana derajat (eksponen terbesar) sama dengan 2, polinomial adalah dari bentuk p (x) = 0, dan terdiri dari istilah kuadratik, a linier dan independen. Itu dinyatakan sebagai berikut:

kapak² + bx + c = 0.

Di mana:

• A, B dan C adalah bilangan real dan ≠ 0.
• kapak² Itu adalah istilah kuadratik, dan "a" adalah koefisien istilah kuadratik.
• BX adalah istilah linier, dan "b" adalah koefisien istilah linier.
• C adalah istilah independen.

Obat anti radang

Secara umum, solusi untuk jenis persamaan ini diberikan ketika membersihkan x persamaan, dan tetap sebagai berikut, yang disebut penyelesaian:

Dapat melayani Anda: teorema binomial

Di sana, (b² - 4ac) disebut diskriminasi dari persamaan dan ekspresi ini menentukan jumlah solusi yang dapat dimiliki oleh persamaan:

• Ya (b² - 4ac) = 0, persamaan akan memiliki solusi tunggal yang dua kali lipat; yaitu, ia akan memiliki dua solusi yang sama.
• Ya (b² - 4ac)> 0, persamaan akan memiliki dua solusi nyata yang berbeda.
• Ya (b² - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

Misalnya, Anda memiliki persamaan 4x² + 10x - 6 = 0, untuk menyelesaikannya terlebih dahulu istilah A, B dan C diidentifikasi, dan kemudian diganti dalam rumus:

A = 4

B = 10

C = -6.

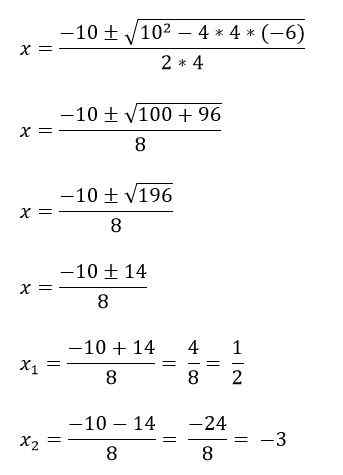
Ada kasus -kasus di mana persamaan polinomial kedua tidak memiliki tiga istilah, dan itulah sebabnya mereka diselesaikan secara berbeda:

• Jika persamaan kuadratik tidak memiliki istilah linier (yaitu, b = 0), persamaan akan dinyatakan sebagai kapak² + C = 0. Untuk menyelesaikannya, X dibersihkan² Dan akar kuadrat diterapkan di setiap anggota, mengingat bahwa dua tanda yang mungkin dimiliki:

kapak² + C = 0.

X² = - c ÷ a

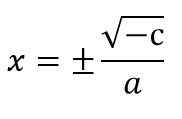
Misalnya, 5 x² - 20 = 0.

5 x² = 20

X² = 20 ÷ 5

x = ± √4

x = ± 2

X₁ = 2.

X₂ = -2.

• Ketika persamaan kuadrat tidak memiliki istilah independen (yaitu, c = 0), persamaan akan dinyatakan sebagai kapak² + Bx = 0. Untuk menyelesaikannya, faktor umum dari X yang tidak diketahui harus diambil pada anggota pertama; Karena persamaan dicocokkan dengan nol, dipenuhi bahwa setidaknya satu faktor akan sama dengan 0:

kapak² + Bx = 0.

x (kapak + b) = 0.

Dengan cara ini, Anda harus:

x = 0.

x = -b ÷ a.

Misalnya: Anda memiliki persamaan 5x² + 30x = 0. Pertama adalah faktor:

5x² + 30x = 0

x (5x + 30) = 0.

Dua faktor dihasilkan yaitu x y (5x + 30). Salah satunya akan dianggap sebagai nol dan yang lainnya diberikan solusi:

X₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

X₂ = -6.

Nilai Tertinggi

Persamaan polinomial derajat utama adalah mereka yang berkisar dari kelas tiga dan seterusnya, yang dapat diekspresikan atau diselesaikan dengan persamaan polinomial umum untuk tingkat apa pun:

Dapat melayani Anda: Koefisien Korelasi: Rumus, Perhitungan, Interpretasi, Contoh

ke_{N *} X^N + ke_{N-1 *} X^N-1 +... + a_{1 *} X¹ + ke_{0 *} X₀ = 0

Ini digunakan karena persamaan dengan derajat yang lebih besar dari dua adalah hasil dari faktorisasi polinomial; Artinya, dinyatakan sebagai penggandaan polinomial kelas satu atau lebih besar, tetapi tanpa akar nyata.

Solusi dari jenis persamaan ini adalah langsung, karena penggandaan dua faktor akan sama dengan nol jika salah satu faktor yang nol (0); Oleh karena itu, masing -masing persamaan polinomial yang ditemukan harus diselesaikan, mencocokkan masing -masing faktornya dengan nol.

Misalnya, Anda memiliki persamaan tingkat ketiga (kubik) x³ + X² +4x + 4 = 0. Untuk menyelesaikannya, Anda harus mengikuti langkah -langkah berikut:

• Istilah dikelompokkan:

X³ + X² +4x + 4 = 0

(X³ + X² ) + (4x + 4) = 0.

• Anggota rusak untuk mendapatkan faktor umum dari yang tidak diketahui:

X² (x + 1) + 4 (x + 1) = 0

(X² + 4)_*(x + 1) = 0.

• Dengan cara ini, dua faktor diperoleh, yang harus sama dengan nol:

(X² + 4) = 0

(x + 1) = 0.

• Dapat dilihat bahwa faktor (x² + 4) = 0 tidak akan memiliki solusi nyata, sedangkan faktor (x + 1) = 0 ya. Karena itu, solusinya adalah:

(x + 1) = 0

x = -1.

Latihan terpecahkan

Selesaikan persamaan berikut:

Latihan Pertama

(2x² + 5)_*(X - 3)_*(1 + x) = 0.

Larutan

Dalam hal ini persamaan dinyatakan sebagai penggandaan polinomial; Artinya, itu diperkaktifkan. Untuk menyelesaikannya, setiap faktor harus sama dengan nol:

2x² + 5 = 0, tidak memiliki solusi.

x - 3 = 0

x = 3.

1 + x = 0

x = - 1.

Dengan cara ini, persamaan yang diberikan memiliki dua solusi: x = 3 dan x = -1.

Latihan kedua

X⁴ - 36 = 0.

Larutan

Polinomial diberikan, yang dapat dijual sebagai perbedaan dalam kotak untuk mencapai solusi yang lebih cepat. Dengan demikian, persamaan tetap:

(X² + 6)_*(X² - 6) = 0.

Untuk menemukan solusi dari persamaan, kedua faktornya sama dengan nol:

(X² + 6) = 0, tidak memiliki solusi.

(X² - 6) = 0

X² = 6

x = ± √6.

Dengan demikian, persamaan awal memiliki dua solusi:

x = √6.

x = - √6.