Properti enegon, cara membuat enegon, contoh

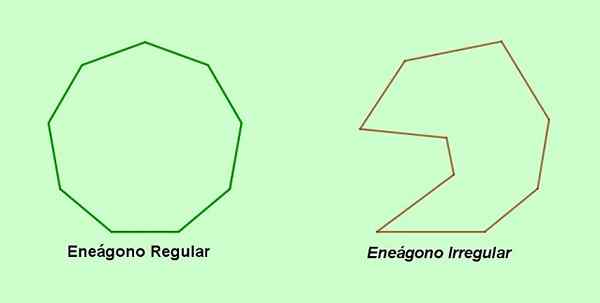
A Enegon Itu adalah poligon sembilan sisi dan sembilan simpul, yang bisa teratur atau tidak. Denominasi Enegon berasal dari bahasa Yunani dan terdiri dari kata -kata Yunani Ennea (sembilan dan Gonon (sudut).

Nama alternatif untuk Poligon Sembilan -Sidang adalah kata non -kata yang berasal dari bahasa Latin nonus (sembilan dan Gonon (puncak). Di sisi lain, jika sisi atau sudut enegon tidak sama satu sama lain, maka ada a Enegon tidak teratur. Jika sebaliknya, sembilan sisi dan sembilan sudut enegon sama, maka itu adalah a Enegon biasa.

Gambar 1. Enegon dan Enegon yang tidak teratur. (Elaborasi sendiri)

[TOC]

Properti Enegon

Untuk poligon sisi N, jumlah sudut internalnya adalah:

(N - 2) * 180º

Di enegon itu akan menjadi n = 9, jadi jumlah sudut internalnya adalah:

SA = (9 - 2) * 180º = 7 * 180º = 1260º

Dalam poligon apa pun, jumlah diagonal adalah:

D = n (n - 3) / 2 dan dalam kasus enegon, seperti n = 9, Anda harus d = 27.

Enegon biasa

Di enegon atau nonagon biasa.

Maka perlu untuk mengukur sudut internal suatu enegon adalah 1260º / 9 = 140º.

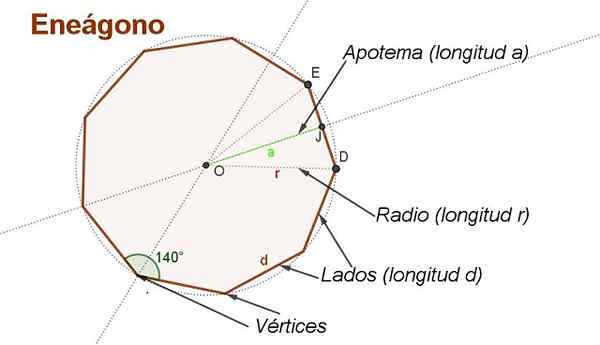Gambar 2. Apothem, radio, sisi, sudut dan simpul enegon biasa. (Elaborasi sendiri)

Untuk menyimpulkan formula area enegon biasa di samping D Lebih mudah untuk membuat beberapa konstruksi tambahan, seperti yang ditunjukkan pada Gambar 2.

Pusatnya SALAH SATU Menggambar mediatrices dari dua sisi yang berdekatan. Tengah SALAH SATU Equidista dari simpul.

Radius panjangnya R Itu adalah segmen yang berjalan dari pusat SALAH SATU Di titik enegon. Radio ditunjukkan pada Gambar 2 Od Dan Oe panjangnya R.

Dapat melayani Anda: simetri

Apothem adalah segmen yang beralih dari tengah ke titik tengah di satu sisi enegon. Misalnya OJ Itu adalah apothem yang panjangnya ke.

Area sisi dan apothem yang dikenal enegon

Kami mempertimbangkan segitiga SYAIR PUJIAN Dari Gambar 2. Area segitiga ini adalah produk dari pangkalannya DARI dengan tinggi OJ dibagi dengan 2:

Daerah SYAIR PUJIAN = (Dari * oj) / 2 = (D * A) / 2

Karena ada 9 segitiga dari area yang sama di Enegon, disimpulkan bahwa area yang sama adalah:

Area Enegon = (9/2) (d * a)

Area enegon yang dikenal

Jika saja panjang enegon diketahui, maka perlu untuk menemukan panjang apothem untuk dapat menerapkan rumus bagian sebelumnya.

Kami mempertimbangkan segitiga Oje Persegi panjang J (Lihat Gambar 2). Jika rasio trigonometri torsi diterapkan, itu diperoleh:

Jadi(∡Oej) = OJ / Misalnya.

Sudut ∡oej = 140º / 2 = 70º, untuk menjadi Eo BISECTOR Sudut internal enegon.

Di samping itu, OJ Itu adalah apothem panjangnya ke.

Lalu sebagai J Itu adalah titik tengah Ed Itu mengikuti itu Ex = d/2.

Mengganti nilai -nilai di atas dalam hubungan garis singgung adalah:

Tan (70º) = A / (d / 2).

Sekarang kita membersihkan panjang apothem:

A = (d/2) Tan (70º).

Hasil sebelumnya diganti dalam formula area untuk mendapatkan:

Area Enegon = (9/2) (d * a) = (9/2)( D * (d/2) Tan (70º))

Akhirnya ada formula yang memungkinkan area enegon reguler diperoleh jika hanya panjang yang diketahui D sisi -sisinya:

Area Enegon = (9/4) D² Tan (70º) = 6.1818 d²

Perimeter dari Enegon biasa diketahui di sisinya

Perimeter poligon adalah jumlah sisinya. Dalam kasus enegon, seperti masing -masing sisi yang mengukur panjangnya D, Perimeternya akan menjadi jumlah sembilan kali D, artinya:

Dapat melayani Anda: persamaan polinomial

Perimeter = 9 D

Perimeter Enegon Mengetahui Radio -nya

Mempertimbangkan segitiga Oje Persegi panjang J (Lihat Gambar 2), alasan trigonometri cosen diterapkan:

cos (∡Oej) = Misalnya / Oe = (d / 2) / r

Dimana kamu diperoleh:

D = 2R cos (70º)

Mengganti hasil ini, formula perimeter diperoleh sebagai fungsi dari jari -jari enegon:

Perimeter = 9 D = 18 r cos (70º) = 6.1564 r

Cara membuat enegon biasa

1- Untuk membangun enegon reguler, dengan aturan dan kompas, didasarkan pada keliling C yang berbatasan dengan enegon. (Lihat Gambar 3)

2- Dua garis tegak lurus ditarik melalui pusat atau keliling. Kemudian persimpangan A dan B dari salah satu garis ditandai dengan keliling.

3- Dengan kompas, membuat pusat di intersepsi B dan membuka setara dengan jari-jari bo.

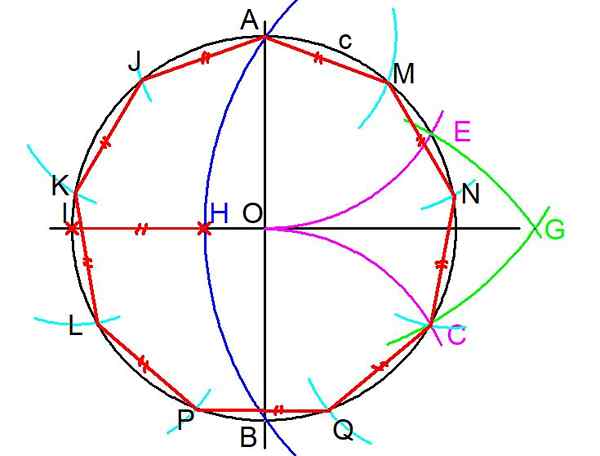Gambar 3. Langkah -langkah untuk membangun enegon biasa. (Elaborasi sendiri)

4- Langkah sebelumnya diulang tetapi membuat pusat di A dan Radio ao sebuah lengkungan ditarik yang mencegat keliling C pada titik e.

5- Dengan pembukaan AC dan tengah dalam busur keliling ditarik. Demikian pula dengan pembukaan dan pusat b lengkungan lain ditarik. Persimpangan kedua lengkungan ini ditandai sebagai g.

6- membuat pusat di g dan dengan ga pembukaan busur ditarik yang mencegat sumbu sekunder (horizontal dalam hal ini) pada titik h. Persimpangan sumbu sekunder ditandai dengan lingkar asli C sebagai i.

7- Panjang segmen IH sama dengan panjang D di sisi enegon.

8- Dengan pembukaan kompas IH = D Lengkungan tengah berturut-turut ditarik ke radio AJ, Centro J Radio AK, KL Radio KL dan Centro L Radio LP.

Itu dapat melayani Anda: transformasi linier: properti, apa saja penggunaan, jenis, contoh

9- Demikian pula, mulai dari A dan di sisi kanan, Radio Arcos IH = D ditarik pada lingkar asli C Points M, N, C dan Q.

10- Akhirnya segmen AJ, JK, KL, LP, AM, MN, NC, CQ dan akhirnya PB digambar.

Perlu dicatat bahwa metode konstruksi tidak sepenuhnya tepat, karena dapat diverifikasi bahwa sisi PB terakhir adalah 0,7% lebih lama dari sisi lain. Sampai saat ini, metode konstruksi dan konstruksi kompas tidak diketahui bahwa 100% tepat.

Contoh

Beberapa contoh yang diselesaikan akan dibahas di bawah ini.

Contoh 1

Anda ingin membangun enegon reguler yang sisi -sisinya berukuran 2 cm. Radio apa yang harus dimiliki oleh radio yang harus dimilikinya, sehingga saat menerapkan konstruksi yang dijelaskan sebelumnya, hasil yang diinginkan diperoleh?

Larutan:

Pada bagian sebelumnya, formula yang menghubungkan jari -jari keliling dengan keliling yang dibatasi dengan dégon reguler D disimpulkan:

D = 2R cos (70º)

Membersihkan r dari ekspresi sebelumnya yang kita miliki:

R = d / (2 cos (70º)) = 1.4619 * D

Mengganti nilai d = 2 cm dalam rumus sebelumnya radius 2,92 cm diperoleh.

Contoh 2

Berapa area dari Enegon sisi 2 cm biasa?

Larutan:

Untuk menjawab pertanyaan ini, Anda harus merujuk pada formula, yang sebelumnya ditunjukkan, yang memungkinkan Anda menemukan area enegon yang diketahui panjang D di sisinya:

Area Enegon = (9/4) D² Tan (70º) = 6.1818 d²

Mengganti D untuk nilainya 2 cm dalam formula anterior diperoleh:

Area Enegon = 24.72 cm

Referensi

1. C. DAN. KE. (2003). Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universitas Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Grup Editorial Patria.
3. Freed, k. (2007). Temukan poligon. Perusahaan Pendidikan Benchmark.
4. Hendrik, v. (2013). Poligon umum. Birkhäuser.
5. Iger. (S.F.). Matematika semester pertama Tacaná. Iger.
6. Jr. Geometri. (2014). Poligon. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Matematika: Penalaran dan Aplikasi (Edisi Kesepuluh). Pendidikan Pearson.
8. Patiño, m. (2006). Matematika 5. Progreso editorial.