Karakteristik energi kinetik, jenis, contoh, latihan

Itu Energi kinetik dari suatu objek adalah apa yang terkait dengan pergerakannya, sehingga objek istirahat tidak memiliki, meskipun jenis energi lainnya dapat dimiliki. Baik kecepatan massa dan objek berkontribusi pada energi kinetik, yang pada prinsipnya dihitung menggunakan persamaan: K = ½ mV²

Di mana K Ini adalah energi kinetik di joule (unit energi dalam sistem internasional), M Itu adalah adonan, dan v Itu adalah kecepatan tubuh. Terkadang, energi kinetik juga dilambangkan sebagai DAN_C salah satu T.

Gambar 1. Mobil gerakan memiliki energi kinetik berdasarkan gerakan mereka. Sumber: Pixabay.

[TOC]

Karakteristik energi kinetik

-Energi kinetik adalah skalar, oleh karena itu nilainya tidak tergantung pada arah atau pengertian di mana objek dipindahkan.

-Itu tergantung pada kuadrat kecepatan, yang berarti bahwa dengan menduplikasi kecepatan, energi kinetiknya tidak duplikat secara sederhana, tetapi meningkat 4 kali. Dan jika melipattigakan kecepatannya, maka energinya dikalikan dengan sembilan dan seterusnya.

-Energi kinetik selalu positif, karena massa dan kuadrat kecepatan dan faktor ½.

-Sebuah objek memiliki energi kinetik atau saat istirahat.

-Berkali -kali mengubah Dalam energi kinetik suatu objek, yang bisa negatif. Misalnya, jika pada awal gerakannya objek lebih cepat dan kemudian mulai berhenti, perbedaannya K_terakhir - K_awal kurang dari 0.

-Jika suatu objek tidak mengubah energi kinetiknya, kecepatannya dan massanya tetap konstan.

Teman-teman

Terlepas dari jenis gerakan apa yang memiliki objek, selama bergerak akan memiliki energi kinetik, apakah itu ditransfer di sepanjang garis lurus, berputar dalam orbit melingkar dari jenis apa pun atau mengalami pergerakan gabungan rotasi dan terjemahan.

Dalam hal ini, jika objek dimodelkan sebagai a partikel, Yaitu, meskipun memiliki massa dimensinya tidak diperhitungkan, energi kinetiknya ½ mV², seperti yang dinyatakan di awal.

Misalnya, energi kinetik bumi dalam gerakan terjemahannya di sekitar matahari, dihitung mengetahui bahwa massanya adalah 6.0 · 10²⁴ kg dengan cepat 3.0 · 10⁴ M/S adalah:

K = ½ 6.0 · 10²⁴ kg x (3.0 · 10⁴ MS)² = 2.7 · 10³³ J.

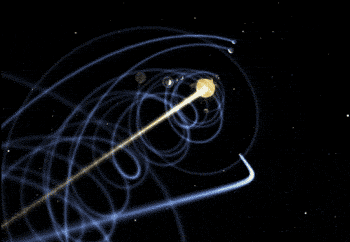
Kemudian, lebih banyak contoh energi kinetik akan ditampilkan untuk berbagai situasi, tetapi untuk saat ini dapat ditanyakan tentang apa yang terjadi dengan energi kinetik dari sistem partikel, karena objek nyata memiliki banyak yang memiliki banyak.

Energi kinetik dari sistem partikel

Ketika Anda memiliki sistem partikel, energi kinetik sistem dihitung dengan menambahkan energi kinetik masing -masing:

K = ½ m₁v₁² + ½ m₂v₂² + ½ m₃v₃² +..

Menggunakan notasi penjumlahan tetap: K = ½ ∑m_yo v_yo², di mana subskrip "I" menunjukkan partikel i-ini dari sistem yang dipermasalahkan, salah satu dari banyak yang membentuk sistem.

Perlu dicatat bahwa ekspresi ini valid, apakah sistem bergerak atau rusak, tetapi dalam kasus terakhir, hubungan antara kecepatan linier dapat digunakan v dan kecepatan sudut Ω dan temukan ekspresi baru K:

v_yo= Ωr_yo

K = ½ ∑m_yo(Ω_yoR_yo)²= ½ ∑m_yoR_yo²Ω_yo²

Dalam persamaan ini, R_yo Itu adalah jarak antara partikel era i dan sumbu rotasi, dianggap tetap.

Dapat melayani Anda: Dwarf merah

Sekarang, misalkan kecepatan sudut masing -masing partikel ini sama, yang terjadi jika jarak di antara mereka tetap konstan, serta jarak ke sumbu rotasi. Jika demikian, subskrip "i" tidak diperlukan untuk Ω Dan ini keluar dari jumlah:

K = ½ Ω² (∑m_yo R_yo²)

Energi rotasi kinetik

Panggilan yo Untuk penjumlahan dalam tanda kurung, ekspresi lain yang lebih kompak ini diperoleh, dikenal sebagai energi rotasi kinetik:

K = ½ iΩ²

Di Sini yo menerima nama momen inersia dari sistem partikel. Momen inersia tergantung, seperti yang kita lihat, tidak hanya pada nilai -nilai massa, tetapi juga pada jarak antara mereka dan sumbu rotasi.

Berdasarkan hal ini, suatu sistem bisa lebih mudah untuk berbalik sehubungan dengan sumbu tertentu daripada sehubungan dengan yang lain. Untuk alasan ini, mengetahui momen inersia suatu sistem membantu menetapkan apa respons Anda nantinya.

Gambar 2. Orang yang berputar di roda korsel memiliki energi rotasi kinetik. Sumber: Pixabay.

Contoh

Gerakan ini umum di alam semesta, melainkan jarang ada partikel istirahat. Pada tingkat mikroskopis, materi terdiri dari molekul dan atom dengan beberapa disposisi tertentu. Tetapi ini tidak berarti bahwa atom dan molekul dari zat istirahat apa pun juga.

Faktanya, partikel di dalam objek bergetar terus menerus. Mereka tidak perlu berpindah dari satu tempat ke tempat lain, tetapi mereka mengalami osilasi. Penurunan suhu berjalan seiring dengan penurunan getaran ini, sehingga nol absolut akan setara dengan penghentian total.

Tetapi mutlak nol belum mampu mencapai sampai sekarang, meskipun di beberapa laboratorium suhu rendah itu sangat dekat untuk mencapainya.

Gerakan ini sering terjadi pada skala galaksi dan atom dan inti atom, sehingga kisaran nilai energi kinetik sangat luas. Mari kita lihat beberapa contoh numerik:

-70 kg orang yang berlari 3.50 m/s memiliki energi kinetik 428.75 J

-Selama ledakan supernova, partikel dengan energi kinetik 10 dipancarkan⁴⁶ J.

-Sebuah buku yang turun dari ketinggian 10 sentimeter mencapai tanah dengan energi kinetik yang setara dengan 1 joule kurang lebih.

-Jika orang dalam contoh pertama memutuskan untuk berjalan pada tingkat 8 m/s, energi kinetiknya meningkat hingga mencapai 2240 J.

-Bola baseball 0 adonan.142 kg diluncurkan di 35.8 km/jam memiliki energi kinetik 91 j.

-Rata -rata, energi kinetik molekul udara adalah 6.1 x 10^{-dua puluh satu} J.

Gambar 3. Ledakan supernova di galaksi cerutu yang terlihat oleh teleskop hubble. Sumber: NASA Goddard.

Teorema kerja - energi kinetik

Pekerjaan yang dilakukan dengan paksa pada suatu objek dapat mengubah gerakannya. Dan dengan melakukannya, energi kinetik bervariasi, mampu meningkatkan atau mengurangi.

Jika partikel atau objek beralih dari titik A ke titik B, pekerjaan W_AB diperlukan sama dengan perbedaan antara energi kinetik yang dimiliki objek di antara titik tersebut B Dan yang ada di intinya KE:

W_AB = K_B - K_KE = ΔK = w_bersih

Simbol "δ" berbunyi "Delta" dan melambangkan perbedaan antara magnitudo akhir dan besarnya awal. Sekarang mari kita lihat kasus -kasus tertentu:

-Jika pekerjaan yang dilakukan pada objek negatif, itu berarti bahwa kekuatan menentang gerakan. Oleh karena itu energi kinetik berkurang.

-Di sisi lain, ketika pekerjaan itu positif, itu berarti kekuatan yang disukai kekuatan dan energi kinetik meningkat.

-Mungkin terjadi bahwa kekuatan tidak bekerja pada objek, yang tidak berarti bahwa itu masih. Dalam hal ini energi kinetik tubuh itu tidak berubah.

Saat bola dilemparkan secara vertikal, selama unggahan gravitasi melakukan pekerjaan negatif dan bola mengerem, tetapi pada rute ke bawah, gravitasi mendukung jatuh dengan meningkatkan kecepatan.

Dapat melayani Anda: Gerakan bujursangkar yang dipercepat secara seragam: Karakteristik, formula

Akhirnya, benda -benda yang memiliki gerakan bujursangkar yang seragam atau gerakan melingkar yang seragam tidak mengalami variasi dalam energi kinetiknya, karena kecepatannya konstan.

Hubungan antara energi kinetik dan momen

Momen linier atau momentum Itu adalah vektor yang dilambangkan P. Seharusnya tidak bingung dengan berat objek, vektor lain yang sering dilambangkan dengan cara yang sama. Momen ini didefinisikan sebagai:

P = m.v

Di mana m adalah massa dan v adalah vektor veloc tubuh. Besarnya momen dan energi kinetik menjaga hubungan tertentu, karena keduanya bergantung pada massa dan kecepatan. Anda dapat dengan mudah menemukan hubungan antara kedua besaran:

K = ½ mV² = (Mv)² / 2m = p² /2m

Hal yang baik tentang menemukan hubungan antara momen dan energi kinetik, atau antara momen dan besaran fisik lainnya, adalah bahwa momen tersebut dipertahankan dalam banyak situasi, seperti selama tabrakan dan situasi kompleks lainnya. Dan ini memfasilitasi menemukan solusi untuk masalah jenis ini.

Konservasi energi kinetik

Energi kinetik suatu sistem tidak selalu dipertahankan, kecuali dalam kasus -kasus tertentu seperti dalam tabrakan elastis sempurna. Mereka yang terjadi antara benda -benda yang hampir tidak dapat dideformasi seperti bola biliar dan partikel subatomik sangat dekat dengan cita -cita ini.

Selama tabrakan elastis sempurna dan dengan asumsi bahwa sistem diisolasi, partikel dapat mentransfer energi kinetik satu sama lain, tetapi dengan kondisi bahwa jumlah energi kinetik individu adalah konstan.

Namun, dalam sebagian besar tabrakan ini tidak terjadi, karena sejumlah energi kinetik sistem diubah menjadi kalori, deformasi atau energi suara.

Meskipun.

Latihan

- Latihan 1

Vas kaca dijatuhkan yang adonannya 2.40 kg dari ketinggian 1.30 m. Hitung energi kinetik Anda tepat sebelum mencapai tanah, tanpa memperhitungkan resistensi udara.

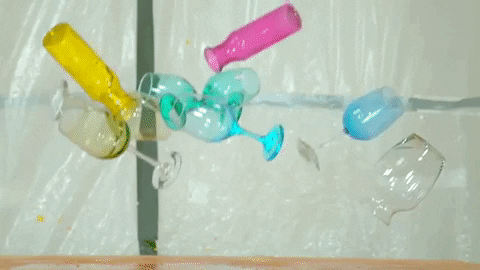
Larutan

Untuk menerapkan persamaan energi kinetik, perlu mengetahui kecepatan v dengan vas tiba di tanah. Ini adalah jatuh gratis dan ketinggian total tersedia H, Oleh karena itu, saat menggunakan persamaan kinematika:

v_F² = v_{salah satu}² +2GH

Dalam persamaan ini, G Itu adalah nilai percepatan gravitasi dan v_{salah satu} Ini adalah kecepatan awal, yang dalam hal ini adalah 0 karena vas itu jatuh, oleh karena itu:

v_F² = 2GH

Anda dapat menghitung kuadrat kecepatan dengan persamaan ini. Perhatikan bahwa kecepatan tidak diperlukan, karena K = ½ mV². Anda juga dapat mengganti kecepatan persegi dalam persamaan K:

K = ½ m (2gh) = mgh

Dan akhirnya dievaluasi dengan data yang disediakan dalam pernyataan:

Dapat melayani Anda: galaksi elips: pembentukan, karakteristik, jenis, contoh

K = 2.40 kg x 9.8 m/s² x 1.30 m = 30.6 j

Sangat menarik untuk dicatat bahwa dalam hal ini, energi kinetik tergantung pada ketinggian dari mana vas turun. Dan seperti yang diharapkan, energi kinetik vas meningkat dari saat jatuhnya dimulai. Itu karena gravitasi melakukan pekerjaan positif pada vas, seperti yang dijelaskan di atas.

- Latihan 2

Truk yang massanya M = 1 250 kg memiliki kecepatan v₀ = 105 km/jam (29.2 m/s). Hitung pekerjaan yang harus dilakukan rem untuk menghentikannya sepenuhnya.

Larutan

Untuk menyelesaikan latihan ini, Anda harus memanfaatkan energi teorema-QUINIC yang berfungsi yang dinyatakan di atas:

W = k_terakhir - K_awal = ΔK

Energi kinetik awal adalah ½ mV_{salah satu}² Dan energi kinetik terakhir adalah 0, karena pernyataan itu mengatakan bahwa truk berhenti sepenuhnya. Dalam hal ini, pekerjaan yang dilakukan oleh rem diinvestasikan secara keseluruhan untuk menghentikan kendaraan. Mempertimbangkannya:

W = -½ mV_{salah satu}²

Sebelum mengganti nilai -nilai, mereka harus dinyatakan dalam satuan sistem internasional, untuk mendapatkan joule saat menghitung pekerjaan:

v₀ = 105 km/jam = 105 km/jam x 1000 m/km x 1 jam/3600 s = 29.17 m/s

Dan nilainya diganti dalam persamaan untuk bekerja:

W = - ½ x 1250 kg x (29.17 m/s)² = -531.805.6 j = -5.3 x 10⁵ J.

Perhatikan bahwa pekerjaan itu negatif, yang masuk akal karena kekuatan rem menentang gerakan yang dibawa kendaraan, membuat energi kinetiknya berkurang.

- Latihan 3

Ada dua mobil yang sedang bergerak. Yang pertama memiliki massa dua kali lebih banyak dari yang kedua, tetapi hanya setengah dari energi kinetiknya. Saat kedua mobil meningkatkan kecepatan mereka 5.0 m/s, energi kinetiknya sama. Apa rapides asli dari kedua mobil?

Larutan

Pada awalnya, mobil 1 memiliki energi kinetik k_1st dan massa m₁, sementara mobil 2 memiliki energi kinetik k₂ dan massa m₂. Diketahui juga bahwa:

M₁ = 2m₂ = 2m

K_1st = ½ k₂

Dengan mengingat hal ini tertulis: K_1st = ½ (2m) v₁²  Dan K₂ = ½ mV₂²

Diketahui itu K_1st = ½ k₂, yang artinya:

K_1st = ½ 2MV₁² = ½ (½ mV₂²)

Karena itu:

2v₁² = ½ v₂²

v₁² = ¼ v₂² → V₁  = V₂ /2

Kemudian dia mengatakan bahwa jika rapides meningkat menjadi 5 m/s energi kinetik disamakan:

½ 2m (v₁ + 5)² = ½ m (v₂+ 5)² → 2 (v₁ + 5)² = (v₂+ 5)²

Hubungan antara kedua rapides diganti:

2 (v₁ + 5)² = (2v₁ + 5)²

Akar kuadrat diterapkan di kedua sisi, untuk membersihkan v₁:

√2 (v₁ + 5) = (2V₁ + 5)

(√2 - 2) v₁ = 5 - √2 × 5 → -0.586 v₁ = -2.071 → V₁ = 3.53 m/s

v₂ = 2 v₁ = 7.07 m/s.

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
2. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 2. Dinamis. Diedit oleh Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6. Ed Prentice Hall.
4. Knight, r.  2017. Fisika untuk Ilmuwan dan Teknik: Pendekatan Strategi. Pearson. 
5. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1-2.