Penentuan keseimbangan translasi, aplikasi, contoh

Dia Keseimbangan translasi Itu adalah keadaan di mana suatu objek secara keseluruhan adalah ketika semua kekuatan yang bekerja di atasnya dikompensasi, menghasilkan gaya batal. Secara matematis itu setara dengan mengatakan itu f₁+ F₂ +  F₃ +.. . = 0, menjadi f₁, F₂,  F₃... pasukan yang terlibat.

Fakta bahwa suatu tubuh dalam keseimbangan translasi tidak berarti bahwa itu harus istirahat. Ini adalah kasus khusus dari definisi sebelumnya. Objek dapat bergerak, tetapi tanpa akselerasi, ini akan menjadi gerakan bujursangkar yang seragam.

Gambar 1. Saldo terjemahan penting untuk sejumlah besar olahraga. Sumber: Pixabay.

Jadi jika tubuh sedang istirahat terus berlanjut. Dan jika Anda sudah memiliki gerakan, itu akan memiliki kecepatan konstan. Secara umum, pergerakan objek apa pun adalah komposisi terjemahan dan rotasi. Terjemahan dapat seperti yang ditunjukkan pada Gambar 2: Linear atau Curvilinear.

Tetapi jika salah satu titik objek diperbaiki, maka satu -satunya kemungkinan bergerak adalah berputar. Contohnya adalah CD, yang pusatnya sudah diperbaiki. CD memiliki kemungkinan untuk berputar di sekitar sumbu yang melewati titik itu, tetapi tidak bergerak.

Ketika objek memiliki titik tetap atau didukung pada permukaan, ada pembicaraan tautan. Tautan berinteraksi membatasi gerakan yang mampu dilakukan objek.

[TOC]

Penentuan keseimbangan translasi

Untuk suatu partikel dalam keseimbangan itu valid untuk memastikan bahwa:

F_R = 0

Atau dalam notasi ringkasan:

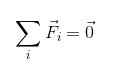
Jelas bahwa untuk suatu tubuh berada dalam keseimbangan translasi, kekuatan yang menindaklanjutinya harus dikompensasi dalam beberapa cara, sehingga hasilnya tidak berlaku.

Dengan cara ini objek tidak akan mengalami akselerasi dan semua partikelnya sedang istirahat atau percobaan terjemahan bujursangkar dengan kecepatan konstan.

Itu dapat melayani Anda: Teori Big Bang: Karakteristik, Tahapan, Bukti, Masalah

Sekarang, jika objek dapat berputar, mereka umumnya akan melakukannya. Itulah sebabnya sebagian besar gerakan terdiri dari kombinasi terjemahan dan rotasi.

Rotasi suatu objek

Ketika keseimbangan rotasi penting, mungkin perlu untuk memastikan bahwa objek tidak berputar. Maka Anda harus mempelajari apakah ada torsi atau momen yang bertindak di atasnya.

Torsi adalah besarnya vektor di mana rotasi bergantung. Mengharuskan kekuatan diterapkan, tetapi titik penerapan ini juga penting. Untuk mengklarifikasi gagasan itu, pertimbangkan objek yang diperluas di mana suatu kekuatan bertindak F Dan mari kita lihat apakah Anda dapat menghasilkan rotasi sehubungan dengan beberapa sumbu atau.

Sudah intuisi bahwa dengan mendorong objek di titik P dengan gaya F, Dimungkinkan untuk membalikkan titik O, dengan arah anti -ulat. Tetapi arah di mana gaya diterapkan juga penting. Misalnya gaya yang diterapkan pada gambar medium tidak akan dapat mengubah objek, meskipun tentu saja dapat memindahkannya.

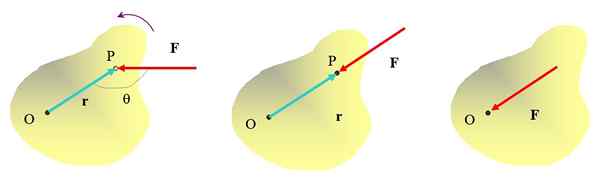Gambar 2. Berbagai cara untuk menerapkan kekuatan pada objek yang luas, hanya pada gambar ekstrem kiri efek rotasi diperoleh. Sumber: Made sendiri.

Terapkan gaya langsung pada titik atau tidak akan digunakan untuk memutar objek juga. Maka jelas bahwa untuk mencapai efek rotasi, gaya harus diterapkan pada jarak tertentu dari sumbu rotasi dan garis aksinya tidak boleh melalui sumbu itu.

Definisi torsi

Torsi atau momen gaya, dilambangkan sebagai τ magnitudo vektor yang bertanggung jawab untuk menyatukan semua fakta ini, didefinisikan sebagai:

τ = r x f

Vektor R Ini diarahkan dari sumbu rotasi ke titik penerapan gaya dan partisipasi sudut antara R dan F adalah penting. Oleh karena itu, besarnya torsi dinyatakan sebagai:

Dapat melayani Anda: Hukum Pertama Newton: Rumus, Eksperimen dan Latihan

τ = r.F.Sen Q

Torsi paling efektif terjadi saat R Dan F Mereka tegak lurus.

Sekarang, jika diinginkan bahwa tidak ada rotasi atau lulus ini dengan akselerasi sudut konstan, perlu bahwa jumlah torsi yang bekerja pada objek adalah nol, analog dengan apa yang dipertimbangkan untuk kekuatan:

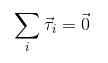
Kondisi keseimbangan

Keseimbangan berarti stabilitas, harmoni dan keseimbangan. Agar pergerakan suatu objek memiliki karakteristik ini, kondisi yang dijelaskan pada bagian sebelumnya harus diterapkan:

1) f₁+ F₂ +  F₃ +.. . = 0

2) τ₁+ τ₂ +  τ₃ +.. . = 0

Kondisi pertama menjamin keseimbangan translasi dan yang kedua rotasi. Keduanya harus dipenuhi jika objek ingin tetap masuk keseimbangan statis (Tidak adanya gerakan apa pun).

Aplikasi

Kondisi keseimbangan berlaku untuk berbagai struktur, karena ketika bangunan atau beragam objek dibangun, dibuat dengan maksud bahwa bagian mereka dipertahankan dalam posisi relatif yang sama satu sama lain. Dengan kata lain, objek itu tidak dilucuti.

Ini penting misalnya ketika membangun jembatan yang tetap kokoh di bawah kaki mereka, atau saat merancang struktur yang dapat dihuni yang tidak mengubah posisi atau memiliki kecenderungan untuk dibuang.

Sementara diyakini bahwa gerakan bubur seragam seragam adalah penyederhanaan yang ekstrem dari gerakan, yang biasanya terjadi sedikit di alam, harus diingat bahwa kecepatan cahaya dalam kekosongan adalah konstan, dan suara di udara juga, jika jika jika jika jika jika suara di udara, jika jika jika jika suara di udara, jika jika jika ada suara, jika jika ada, jika ada, menganggap homogen terhadap lingkungan.

Dalam banyak struktur seluler yang dibuat oleh manusia, penting bahwa kecepatan konstan dipertahankan: misalnya, pada tangga mekanik dan jalur perakitan.

Ini dapat melayani Anda: Hukum Kedua Termodinamika: Rumus, Persamaan, Contoh

Contoh keseimbangan translasi

Ini adalah latihan klasik dari ketegangan yang menahan lampu dalam keseimbangan. Diketahui bahwa lampu tersebut memiliki berat 15 kg. Temukan besaran ketegangan yang diperlukan untuk menjaganya di posisi ini.

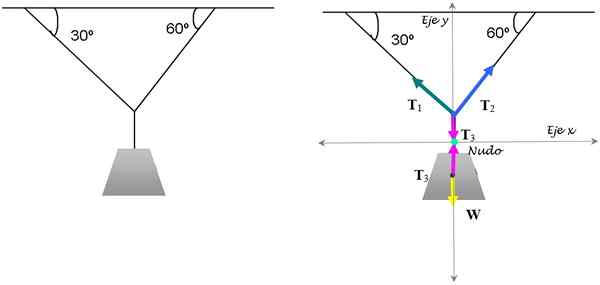Gambar 3. Saldo lampu dijamin dengan menerapkan kondisi keseimbangan translasi. Sumber: Made sendiri.

Larutan

Untuk menyelesaikannya, kami fokus pada simpul di mana tiga senar bersatu. Diagram tubuh bebas masing -masing untuk simpul dan untuk lampu ditunjukkan pada gambar di atas.

Berat lampu W = 5 kg . 9.8 m/s² = 49 n. Agar lampu berada dalam keseimbangan, cukup bahwa kondisi keseimbangan pertama dipenuhi:

T₃ - W = 0

T₃ = W = 49 n.

Ketegangan T₁ Dan T₂ Mereka harus membusuk:

T_1y + T_{2 dan} - T₃ = 0 (Musim Panas Pasukan di sepanjang sumbu Y))

-T_1x +T_2x = 0 (Musim Panas Pasukan di sepanjang sumbu X)

Menerapkan trigonometri:

T₁.Cos 60º +t₂ .Cos 30º = 49

- T₁.sen60º +t₂.Sen30º = 0

Ini adalah sistem dua persamaan dengan dua yang tidak diketahui, yang jawabannya adalah: T₁ = 24.5 n Dan T₂ = 42.4 n.

Referensi

1. Rex, a. 2011. Dasar -dasar fisika. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7^ma. Ed. Pembelajaran Cengage. 120 - 124.
3. Serway, r., Vulle, c. 2011. Dasar -dasar fisika. 9^na Ed. Pembelajaran Cengage. 99-112.
4. Tippens, hlm. 2011. Fisika: Konsep dan Aplikasi. Edisi ke -7. Bukit MacGraw. 71 - 87.
5. Walker, J. 2010. Fisika. Addison Wesley. 332 -346.