Estimasi Standar Kesalahan Bagaimana Dihitung, Contoh, Latihan

Dia Kesalahan Estimasi Standar Ukur penyimpangan dalam nilai populasi sampel. Artinya, kesalahan estimasi standar mengukur variasi yang mungkin dari rata -rata sampel sehubungan dengan nilai sebenarnya dari rata -rata populasi.

Misalnya, jika Anda ingin mengetahui usia rata -rata populasi suatu negara (rata -rata populasi) Sekelompok kecil penduduk diambil, yang akan kami sebut "pertunjukan". Darinya usia rata -rata (rata -rata sampel) diekstraksi dan diasumsikan bahwa populasi memiliki usia rata -rata dengan kesalahan estimasi standar yang bervariasi lebih atau kurang.

M. W. Toews [CC dengan 2.5 (https: // createveCommons.Org/lisensi/oleh/2.5)]

Perlu dicatat bahwa penting untuk tidak membingungkan standar deviasi dengan kesalahan standar dan kesalahan estimasi standar:

1- Deviasi standar adalah ukuran dispersi data; yaitu, ini adalah ukuran variabilitas populasi.

2- Kesalahan standar adalah ukuran variabilitas sampel, dihitung berdasarkan standar deviasi populasi.

3- Kesalahan estimasi standar adalah ukuran kesalahan yang dibuat saat mengambil rata-rata sampel sebagai perkiraan rata-rata populasi.

[TOC]

Bagaimana itu dihitung?

Kesalahan estimasi standar dapat dihitung untuk semua langkah yang diperoleh dalam sampel (misalnya, kesalahan estimasi rata -rata standar atau kesalahan standar estimasi standar deviasi) dan mengukur kesalahan yang dibuat ketika memperkirakan ukuran populasi yang sebenarnya dari nilai sampelnya

Dari kesalahan estimasi standar, interval kepercayaan dari ukuran yang sesuai dibangun.

Dapat melayani Anda: matriks terbalik: perhitungan dan olahraga diselesaikan

Struktur umum formula untuk kesalahan estimasi standar adalah sebagai berikut:

Kesalahan estimasi standar = ± koefisien kepercayaan * Kesalahan standar

Koefisien kepercayaan = batas nilai statistik sampel atau distribusi pengambilan sampel (Normal atau Gauss Bell, Student T, antara lain) untuk interval probabilitas tertentu.

Kesalahan standar = standar deviasi populasi dibagi dengan akar kuadrat dari ukuran sampel.

Koefisien kepercayaan menunjukkan jumlah kesalahan standar yang bersedia menambah dan mengurangi yang disesuaikan untuk memiliki tingkat kepercayaan tertentu dalam hasil.

Contoh perhitungan

Asumsikan bahwa Anda mencoba memperkirakan proporsi orang dalam populasi yang memiliki perilaku A, dan Anda ingin memiliki kepercayaan 95% terhadap hasil mereka.

Sampel n orang diambil dan proporsi sampel P dan komplemennya ditentukan.

Kesalahan Estimasi Standar (EEE) = ± Koefisien kepercayaan * Kesalahan Standar

Koefisien kepercayaan = z = 1.96.

Kesalahan standar = akar kuadrat dari alasan antara produk proporsi sampel untuk komplemennya dan ukuran sampel n.

Dari kesalahan estimasi standar, interval di mana proporsi populasi atau proporsi sampel sampel lain yang dapat dibentuk dari populasi tersebut ditetapkan, dengan tingkat kepercayaan 95%:

P -EEE ≤ Proporsi Populasi ≤ P + EEE

Latihan terpecahkan

Latihan 1

1- Asumsikan bahwa Anda mencoba memperkirakan proporsi orang dalam populasi yang memiliki preferensi untuk formula susu yang diperkaya, dan Anda ingin memiliki kepercayaan 95% dalam hasil mereka.

Dapat melayani Anda: Divisi sintetis

Sampel 800 orang diambil dan ditentukan bahwa 560 orang dalam sampel memiliki preferensi untuk formula susu yang diperkaya. Tentukan interval di mana proporsi populasi dapat diharapkan dan proporsi sampel lain yang dapat diambil dari populasi, dengan kepercayaan 95%

a) Mari kita menghitung proporsi sampel P dan komplemennya:

P = 560/800 = 0.70

Q = 1 -p = 1 -0.70 = 0.30

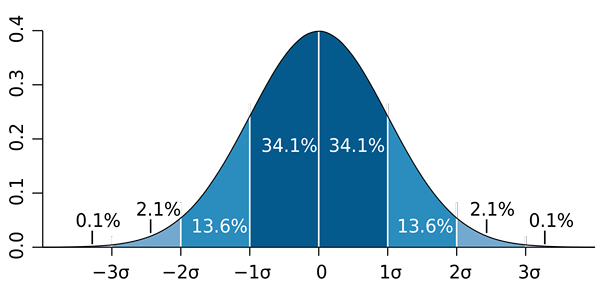
b) Diketahui bahwa proporsi mendekati distribusi normal ke sampel ukuran besar (lebih dari 30). Kemudian, aturan SO yang disebut 68 - 95 - 99 diterapkan.7 dan Anda harus:

Koefisien kepercayaan = z = 1.96

Kesalahan standar = √ (p*q/n)

Kesalahan Estimasi Standar (EEE) = ± (1.96)*√ (0.70)*(0.30)/800) = ± 0.0318

c) Dari kesalahan estimasi standar, interval di mana proporsi populasi diharapkan dengan tingkat kepercayaan 95% ditetapkan:

0.70 -0.0318 ≤ proporsi populasi ≤ 0.70 + 0.0318

0.6682 ≤ proporsi populasi ≤ 0.7318

Anda dapat mengharapkan proporsi sampel 70% berubah hingga 3.18 poin persentase jika mengambil sampel yang berbeda dari 800 orang atau proporsi sebenarnya dari populasi adalah antara 70 - 3.18 = 66.82% dan 70 + 3.18 = 73.18%.

Latihan 2

2- Kami akan mengambil dari Spiegel dan Stephens, 2008, studi kasus berikut:

Dari total nilai matematika dari mahasiswa tahun pertama universitas, sampel acak dari 50 kualifikasi diambil di mana rata -rata yang ditemukan adalah 75 poin dan standar deviasi, 10 poin. Apa batasan kepercayaan 95% untuk estimasi rata -rata kualifikasi matematika universitas?

Itu dapat melayani Anda: apa hubungan antara area belah ketupat dan persegi panjang?

a) Mari kita menghitung kesalahan estimasi standar:

Koefisien kepercayaan 95%= z = 1.96

Kesalahan standar = s/√n

Kesalahan Estimasi Standar (EEE) = ± (1.96)*(10√50) = ± 2.7718

b) Dari kesalahan estimasi standar, interval di mana rata -rata populasi atau rata -rata sampel lain 50 ditetapkan, dengan tingkat kepercayaan 95%:

50 -2.7718 ≤ rata -rata populasi ≤ 50 + 2.7718

47.2282 ≤ rata -rata populasi ≤ 52.7718

c) Anda dapat mengharapkan rata -rata sampel berubah menjadi 2.7718 poin Jika sampel yang berbeda dari 50 nilai diambil atau rata -rata nyata dari nilai matematika populasi universitas adalah antara 47.2282 poin dan 52.7718 poin.

Referensi

1. Abira, v. (2002). Deviasi standar dan kesalahan standar. Majalah Semergen. Web pulih.Arsip.org.
2. Rumsey, d. (2007). Statistik menengah untuk boneka. Wiley Publishing, Inc.
3. Salinas, h. (2010). Statistik dan probabilitas. Pulih dari mat.Uda.Cl.
4. Sokal, r.; Rohlf, f. (2000). Biometri. Prinsip dan Praktik Statistik dalam Penelitian Biologis. Ed ketiga. Edisi Blume.
5. Spiegel, m.; Stephens, l. (2008). Statistik. Edisi keempat. McGraw-Hill/Inter-American dari Meksiko. KE.
6. Wikipedia. (2019). 68-95-99.7 aturan. Diterima dari.Wikipedia.org.
7. Wikipedia. (2019). Kesalahan standar. Diterima dari.Wikipedia.org.