Sejarah statistik inferensial, karakteristik, untuk apa, contohnya

Itu Statistik inferensial atau statistik deduktif adalah salah satu yang menyimpulkan karakteristik populasi dari sampel yang diekstraksi darinya, melalui serangkaian teknik analisis. Dengan informasi yang diperoleh, model diuraikan yang kemudian memungkinkan prediksi tentang perilaku populasi tersebut.

Oleh karena itu, statistik inferensial telah menjadi sains nomor satu untuk menawarkan rezeki dan instrumen yang dibutuhkan disiplin ilmu yang tak terhitung jumlahnya, saat membuat keputusan.

Fisika, Kimia, Biologi, Teknik, dan Ilmu Sosial, terus menerus mendapat manfaat dari alat -alat ini ketika mereka membuat model dan desain mereka dan mengimplementasikan eksperimen.

[TOC]

Sejarah Singkat Statistik Inferensial

Statistik muncul pada zaman kuno karena kebutuhan orang untuk mengatur berbagai hal dan mengoptimalkan sumber daya. Sebelum penemuan penulisan, catatan jumlah orang dan ternak dilakukan, melalui simbol -simbol yang direkam dalam batu.

Kemudian, penguasa Cina, Babilonia dan Mesir meninggalkan data tentang jumlah tanaman dan jumlah penduduk, yang direkam pada tablet tanah liat, kolom dan monumen.

Rum

Ketika Roma menjalankan domainnya di Mediterania, biasa bagi pihak berwenang untuk melakukan sensus setiap lima tahun. Faktanya, kata "statistik" berasal dari kata Italia statista, Apa artinya mengekspresikan.

Secara paralel, di Amerika kekaisaran pra -Kolumbia yang hebat juga membawa catatan serupa.

Abad Pertengahan

Selama Abad Pertengahan Pemerintah Eropa, serta Gereja, mendaftarkan properti Bumi. Kemudian mereka melakukan hal yang sama dengan kelahiran, baptisan, pernikahan dan kematian.

Usia modern

Statistik Inggris John Graunt (1620-1674) adalah yang pertama membuat prediksi berdasarkan daftar tersebut, seperti berapa banyak orang yang bisa meninggal karena penyakit tertentu dan perkiraan proporsi kelahiran wanita dan pria. Oleh karena itu, bapak demografi dipertimbangkan.

Usia kontemporer

Kemudian, dengan munculnya teori probabilitas, statistik tidak lagi menjadi kumpulan teknik organisasi dan mencapai ruang lingkup yang tidak terduga sebagai ilmu prediktif.

Dengan demikian, para ahli mampu.

Karakteristik

Di bawah ini kami memiliki karakteristik yang paling relevan dari cabang statistik ini:

- Studi Statistik Inferensial Suatu populasi mengambil sampel yang representatif.

- Pemilihan sampel dilakukan melalui prosedur yang berbeda, yang paling tepat adalah mereka yang memilih komponen secara acak. Dengan demikian, setiap elemen populasi memiliki kemungkinan yang sama dipilih dan dengan itu, bias yang tidak diinginkan dihindari.

Dapat melayani Anda: cara mengonversi dari km/h a m/s? Latihan terpecahkan

- Untuk mengatur informasi yang dikumpulkan, ia menggunakan statistik deskriptif.

- Pada sampel, variabel statistik dihitung yang berfungsi untuk memperkirakan sifat -sifat populasi.

- Statistik inferensial atau deduktif memanfaatkan teori probabilitas untuk mempelajari peristiwa acak, yaitu, yang muncul secara kebetulan. Setiap peristiwa diberi probabilitas kejadian tertentu.

- Bangun hipotesis -Suposisi- tentang parameter populasi dan kontraskan, untuk mengetahui apakah mereka benar atau tidak dan juga menghitung tingkat kepercayaan respons, yaitu, ia menawarkan margin kesalahan. Prosedur pertama dipanggil tes hipotesis, Sedangkan margin kesalahan adalah interval kepercayaan.

Untuk apa statistik deskriptif? Aplikasi

Statistik inferensial: penting dalam membuat keputusan dan kontrol kualitas

Belajar secara keseluruhan populasi dapat menuntut banyak sumber daya dalam uang, waktu dan upaya. Lebih disukai untuk mengambil sampel representatif yang jauh lebih mudah dikelola, mengumpulkan data melalui mereka dan membuat hipotesis atau asumsi tentang perilaku sampel.

Setelah hipotesis ditetapkan dan validitasnya dikontraskan, hasilnya meluas ke populasi dan digunakan untuk membuat keputusan.

Mereka juga membantu menciptakan model populasi itu, untuk membuat proyeksi di masa depan. Itulah sebabnya statistik inferensial adalah ilmu yang sangat berguna untuk:

Sosiologi dan studi demografis

Ini adalah bidang aplikasi yang ideal, karena teknik statistik berlaku dengan gagasan membangun berbagai model perilaku manusia. Sesuatu yang apriori cukup rumit, karena banyak variabel mengintervensi.

Dalam politik banyak yang digunakan dalam waktu pemilihan untuk mengetahui kecenderungan suara pemilih, dengan cara ini para pihak merancang strategi.

Rekayasa

Metode statistik inferensial banyak digunakan dalam rekayasa, aplikasi yang paling penting adalah kontrol kualitas dan pengoptimalan proses, misalnya, meningkatkan waktu dalam melaksanakan tugas, serta dalam pencegahan kecelakaan kerja.

Ekonomi dan Administrasi Bisnis 

Dengan metode deduktif, proyeksi dapat dilakukan tentang pengoperasian perusahaan, tingkat penjualan yang diharapkan, serta membantu saat membuat keputusan.

Misalnya, teknik Anda dapat digunakan untuk memperkirakan reaksi pembeli terhadap produk baru, hampir diluncurkan ke pasar.

Ini juga berfungsi untuk mengevaluasi apa modifikasi dalam kebiasaan konsumsi orang, diberikan peristiwa penting, seperti epidemi covid.

Contoh statistik inferensial

Contoh 1

Masalah statistik deduktif sederhana adalah sebagai berikut: Seorang guru matematika bertanggung jawab atas 5 bagian aljabar dasar di universitas dan memutuskan untuk menggunakan catatan rata -rata satu bagian mereka untuk memperkirakan rata -rata dari semuanya.

Dapat melayani Anda: perkiraan pengukuran figur amorf: contoh dan olahragaBetapapun besar populasi dapat dipelajari melalui sampel yang representatif. Sumber: Pixabay.

Kemungkinan lain adalah mengambil sampel dari setiap bagian, mempelajari karakteristiknya dan memperluas hasilnya ke semua bagian.

Contoh 2

Manajer toko pakaian untuk wanita ingin tahu berapa banyak blus tertentu akan dijual selama musim panas. Untuk melakukan ini, menganalisis penjualan garmen selama dua minggu pertama musim ini dan dengan demikian menentukan tren.

Konsep dasar dalam statistik inferensial

Ada beberapa konsep utama, termasuk yang berasal dari teori probabilitas, yang perlu untuk memahami semua ruang lingkup teknik ini. Beberapa, sebagai populasi dan sampel, kami telah menyebutkan di seluruh teks.

Peristiwa

Suatu peristiwa atau acara adalah sesuatu yang terjadi, dan itu dapat memiliki beberapa hasil. Contoh acara dapat meluncurkan mata uang dan ada dua hasil yang mungkin: wajah atau segel.

Ruang sampel

Itu adalah himpunan semua hasil yang mungkin dari suatu acara.

Populasi dan sampel

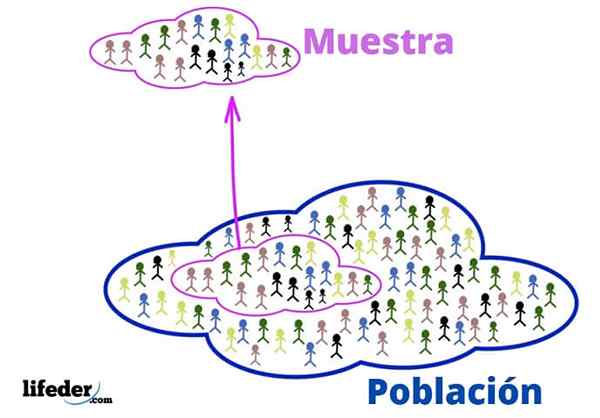Populasi dan sampel

Populasi adalah alam semesta untuk belajar. Mereka tidak harus tentang orang yang hidup atau makhluk, karena populasi, dalam statistik, dapat terdiri dari objek atau ide.

Untuk bagiannya, sampel adalah subset dari populasi, diekstraksi dengan hati -hati untuk menjadi representatif.

Contoh

Ini adalah himpunan teknik di mana sampel dipilih dari populasi tertentu. Pengambilan sampel dapat acak jika metode probabilistik digunakan untuk memilih sampel, atau tidak probabilistik, jika analis memiliki kriteria seleksi sendiri, menurut pengalaman mereka.

Variabel statistik

Set nilai yang dapat memiliki karakteristik populasi. Mereka diklasifikasikan dalam beberapa cara, misalnya mereka bisa bijaksana atau berkelanjutan. Juga, menurut sifat mereka, mereka bisa kualitatif atau kuantitatif.

Distribusi probabilitas

Fungsi probabilitas yang menggambarkan perilaku sejumlah besar sistem dan situasi yang diamati di alam. Yang paling terkenal adalah distribusi Gaussian atau Distribusi Gauss dan Binomial.

Parameter dan statistik 

Teori estimasi menetapkan bahwa ada hubungan antara nilai -nilai populasi dan sampel yang diambil dari populasi tersebut. Itu parameter Mereka adalah karakteristik populasi yang tidak kita ketahui tetapi kita ingin memperkirakan: misalnya rata -rata dan standar deviasi.

Untuk bagiannya, statistik adalah karakteristik sampel, misalnya rata -rata dan standar deviasi.

Sebagai contoh, anggaplah bahwa populasi terdiri dari semua anak muda antara 17 dan 30 tahun komunitas, dan diinginkan untuk mengetahui proporsi mereka yang saat ini dalam pendidikan tinggi. Ini akan menjadi parameter populasi yang harus ditentukan.

Dapat melayani Anda: interpolasi linier

Untuk memperkirakannya, sampel acak dari 50 orang muda dipilih dan proporsi mereka belajar di universitas atau Institut Pendidikan Tinggi dihitung. Proporsi ini adalah statistik.

Jika penelitian ini dilakukan, ditentukan bahwa 63 % dari 50 orang muda belajar lebih tinggi, ini adalah populasi yang diperkirakan, dibuat dari sampel.

Ini hanyalah contoh dari apa yang dapat dilakukan statistik inferensial. Ini dikenal sebagai perkiraan, tetapi ada juga teknik untuk memprediksi variabel statistik, serta membuat keputusan.

Hipotesis statistik

Itu adalah dugaan yang dibuat mengenai nilai rata -rata dan standar deviasi beberapa karakteristik populasi. Kecuali populasi sepenuhnya diperiksa, ini adalah nilai yang tidak diketahui.

Tes hipotesis

Adalah asumsi yang dibuat tentang parameter populasi yang valid? Untuk mengetahuinya, diverifikasi apakah hasil dari sampel mendukungnya atau tidak, jadi perlu untuk merancang tes hipotesis.

Ini adalah langkah umum untuk melakukan satu:

Langkah 1

Identifikasi jenis distribusi yang diharapkan diikuti oleh populasi.

Langkah 2

Naikkan dua hipotesis, dilambangkan sebagai h_{salah satu} dan H₁. Yang pertama adalah hipotesis nol di mana kami mengasumsikan bahwa parameter memiliki nilai tertentu. Yang kedua adalah Hipotesis alternatif yang merupakan nilai yang berbeda dari hipotesis nol. Jika ini ditolak, hipotesis alternatif diterima.

Langkah 3

Menetapkan margin yang dapat diterima untuk perbedaan antara parameter dan statistik. Mereka jarang identik, meskipun mereka diharapkan sangat dekat.

Langkah 4

Mengusulkan kriteria untuk menerima atau menolak hipotesis nol. Untuk ini, statistik uji digunakan yang bisa menjadi rata -rata. Jika nilai rata -rata berada dalam batas tertentu, hipotesis nol diterima, jika tidak maka ditolak.

Langkah 5

Sebagai langkah terakhir diputuskan apakah hipotesis nol diterima atau tidak.

Tema yang menarik

Cabang Statistik.

Variabel statistik.

Populasi dan sampel.

Statistik deskriptif.

Referensi

1. Berenson, m. 1985.Statistik untuk Administrasi dan Ekonomi, Konsep dan Aplikasi. Inter -American Editorial.
2. Canavos, g. 1988. Probabilitas dan Statistik: Aplikasi dan Metode. Bukit McGraw.
3. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Pembelajaran Cengage.
4. Riwayat statistik. Pulih dari: eumeed.bersih.
5. Ibañez, hlm. 2010. Matematika II. Pendekatan kompetensi. Pembelajaran Cengage.
6. Levin, r. 1981. Statistik untuk administrator. Prentice Hall.
7. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.