Rumus dan persamaan kesalahan pengambilan sampel, perhitungan, contoh
- 1572
- 52
- Dewey Runolfsdottir
Dia Kesalahan pengambilan sampel salah satu kesalahan sampel Dalam statistik, itu adalah perbedaan antara nilai rata -rata sampel sehubungan dengan nilai rata -rata dari total populasi. Untuk mengilustrasikan gagasan itu, mari kita bayangkan bahwa total populasi kota adalah satu juta, dari mana Anda menginginkan sepatu rata -rata, di mana seribu orang diambil secara acak.
Ukuran rata -rata yang timbul dari sampel tidak harus bertepatan dengan total populasi, meskipun jika sampel tidak bias, nilainya harus dekat. Perbedaan antara nilai rata -rata sampel ini dan dari total populasi adalah kesalahan sampel.
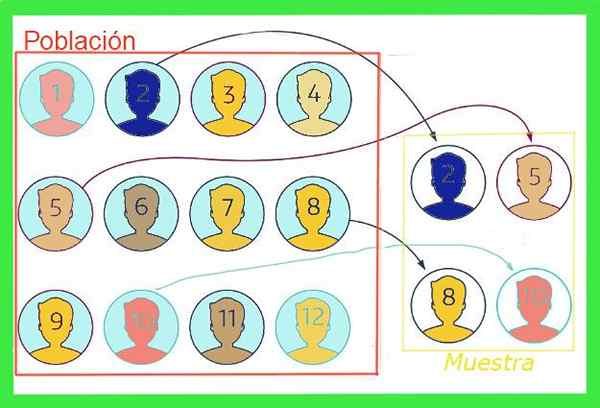
 Gambar 1. Karena sampel adalah subset dari total populasi, rata -rata sampel memiliki margin kesalahan. Sumber: f. Zapata.
Gambar 1. Karena sampel adalah subset dari total populasi, rata -rata sampel memiliki margin kesalahan. Sumber: f. Zapata. Secara umum, nilai rata -rata dari total populasi tidak diketahui, tetapi ada teknik untuk mengurangi kesalahan dan formula tersebut untuk memperkirakan Contoh margin kesalahan yang akan dipamerkan dalam artikel ini.
[TOC]
Rumus dan Persamaan
Mari kita taruh, bahwa Anda ingin mengetahui nilai rata -rata fitur terukur tertentu X Dalam ukuran populasi N, tapi bagaimana caranya N Sejumlah besar tidak layak untuk mempelajari total populasi, jadi kami melanjutkan untuk mengambil a sampel alearory ukuran N<
Nilai rata -rata sampel dilambangkan dengan dan nilai rata -rata dari total populasi menunjukkannya untuk surat Yunani μ (Bunyinya Mu atau miu).
Misalkan mereka diambil M Total sampel populasi N, Semua dengan ukuran yang sama N Dengan nilai rata -rata
Nilai rata -rata ini tidak akan identik satu sama lain dan semuanya akan berada di sekitar nilai populasi rata -rata μ. Dia Contoh margin kesalahan e menunjukkan pemisahan yang diharapkan dari nilai rata -rata sehubungan dengan Nilai populasi rata -rata μ dalam persentase tertentu yang disebut Level kepercayaan γ (Gamma).
Dapat melayani Anda: aditif terbalikDia Margin kesalahan standar ε dari sampel ukuran N adalah:
ε = σ/√n
Di mana σ adalah standar deviasi (Akar kuadrat dari varian), yang dihitung dengan rumus berikut:
σ = √ [(x -)2/(N - 1)]
Arti dari Margin kesalahan standar ε adalah sebagai berikut:
Dia nilai tengah diperoleh dengan ukuran sampel N dipahami dalam interval ( - ε, + ε) dengan tingkat kepercayaan diri 68,3%.
Cara menghitung kesalahan pengambilan sampel
Pada bagian sebelumnya, formula diberikan untuk menemukan rentang kesalahan standar sampel n, di mana kata standar menunjukkan bahwa itu adalah margin kesalahan dengan 68% kepercayaan.
Ini menunjukkan bahwa jika banyak sampel dengan ukuran yang sama diambil N, 68% dari mereka akan memberikan nilai rata -rata dalam kisaran [ - ε, + ε].
Ada aturan sederhana, disebut Aturan 68-95-99.7 yang memungkinkan kita menemukan margin Contoh kesalahan e Untuk tingkat kepercayaan diri 68%, 95% Dan 99,7% Mudah, karena margin ini adalah 1⋅ε, 2⋅ε dan 3⋅ε masing -masing.
Untuk tingkat kepercayaan diri γ
Jika dia Level kepercayaan γ Ini bukan salah satu dari yang di atas, jadi kesalahan pengambilan sampel adalah standar deviasi σ dikalikan dengan faktor Zγ, yang diperoleh melalui prosedur berikut:
1.- Pertama tingkat signifikansi α yang dihitung dari Level kepercayaan γ Melalui hubungan berikut: α = 1 - γ
Dapat melayani Anda: Teorema Bayes2.- Maka Anda harus menghitung nilai 1 - α/2 = (1 + γ)/2, yang sesuai dengan frekuensi normal yang terakumulasi antara -∞ dan Zγ, Dalam distribusi normal atau Gaussian ditiru f (z), yang definisinya dapat dilihat pada Gambar 2.
3.- Persamaannya diselesaikan F (zγ) = 1 - α/2 Melalui tabel distribusi normal (terakumulasi) F, o Melalui aplikasi komputer yang memiliki fungsi Gaussian terbalik yang ditiru F-1.
Dalam kasus terakhir yang Anda miliki:
Zγ = g-1(1 - α/2).
4.- Akhirnya, formula untuk kesalahan pengambilan sampel ini dengan tingkat keandalan diterapkan γ:
E = Zγ⋅(σ/√n)
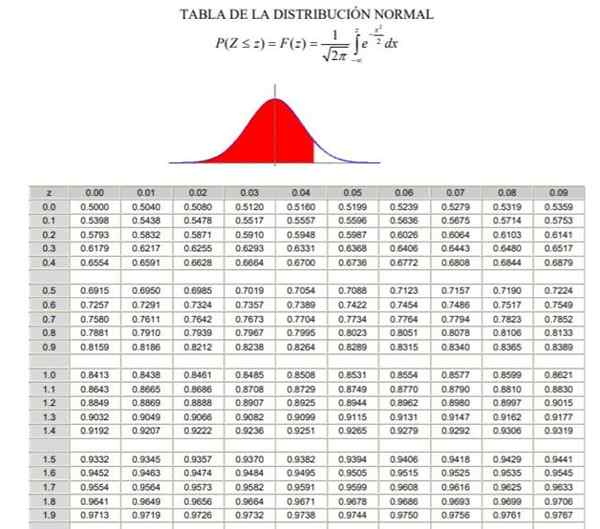 Gambar 2. Tabel distribusi normal. Sumber: Wikimedia Commons.
Gambar 2. Tabel distribusi normal. Sumber: Wikimedia Commons. Contoh
- Contoh 1
Hitung Margin kesalahan standar Berat rata -rata sampel 100 bayi baru lahir. Perhitungan berat rata -rata adalah = 3.100 kg dengan standar deviasi σ = 1.500 kg.
Larutan
Dia Margin kesalahan standar adalah ε = σ/√n = (1.500 kg)/√100 = 0,15 kg. Yang berarti bahwa dengan data ini dapat disimpulkan bahwa berat 68% dari bayi baru lahir adalah antara 2.950 kg dan 3.25 kg.
- Contoh 2
Menentukan margin kesalahan sampel dan dan kisaran berat 100 bayi baru lahir dengan tingkat kepercayaan 95% jika berat rata -rata adalah 3.100 kg dengan standar deviasi σ = 1.500 kg.
Larutan
Jika Peraturan 68; 95; 99.7 → 1⋅ε; 2⋅ε; 3⋅ε, Kamu punya:
E = 2⋅ε = 2⋅0.15 kg = 0,30 kg
Dengan kata lain, 95% bayi baru lahir akan memiliki peso antara 2.800 kg dan 3.400 kg.
- Contoh 3
Tentukan kisaran PESO dari Bayi Baru Lahir Contoh 1 dengan margin kepercayaan 99,7%.
Dapat melayani Anda: rhomboid: karakteristik, cara mengeluarkan perimeter dan areaLarutan
Kesalahan sampel dengan kepercayaan 99,7% 3 σ/√n, bahwa untuk contoh kami adalah E = 3 *0,15 kg = 0,45 kg. Dari sini disimpulkan bahwa 99,7% bayi baru lahir akan memiliki peso antara 2.650 kg dan 3.550 kg.
- Contoh 4
Tentukan faktornya Zγ Untuk tingkat reliabilitas 75%. Tentukan margin kesalahan pengambilan sampel dengan tingkat keandalan ini untuk kasus yang diangkat pada Contoh 1.
Larutan
Dia tingkat kepercayaan diri adalah γ = 75% = 0,75 yang berkaitan dengan tingkat signifikansi α melalui hubungan γ= (1 - α), sehingga tingkat signifikansinya α = 1 - 0,75 = 0,25.
Ini berarti bahwa akumulasi probabilitas normal antara -∞ dan Zγ adalah:
P (z ≤ Zγ ) = 1 - 0.125 = 0,875
Apa yang sesuai dengan nilai Zγ 1.1503, seperti yang ditunjukkan pada Gambar 3.
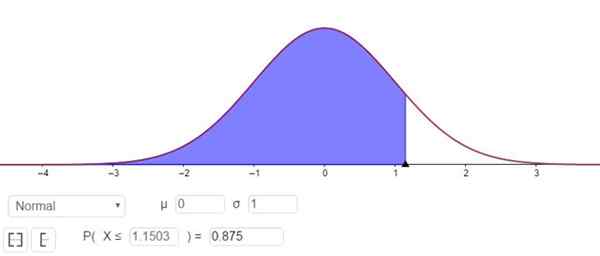 Gambar 3. Penentuan faktor zγ yang sesuai dengan tingkat kepercayaan 75%. Sumber: f. Zapata melalui Geogebra.
Gambar 3. Penentuan faktor zγ yang sesuai dengan tingkat kepercayaan 75%. Sumber: f. Zapata melalui Geogebra. Dengan kata lain, kesalahan pengambilan sampel adalah E = Zγ⋅(σ/√n)= 1.15⋅(σ/√n).
Saat diterapkan pada data contoh 1, itu memberikan kesalahan:
E = 1,15*0,15 kg = 0,17 kg
Dengan tingkat kepercayaan 75%.
- Latihan 5
Berapa tingkat kepercayaan jika zα/2 = 2.4 ?
Larutan
P (z ≤ zα/2 ) = 1 - α/2
P (z ≤ 2.4) = 1 - α/2 = 0,9918 → α/2 = 1 - 0,9918 = 0,0082 → α = 0,0164
Tingkat signifikansi adalah:
α = 0,0164 = 1,64%
Dan akhirnya, tingkat kepercayaan tetap:
1- α = 1 - 0,0164 = 100% - 1,64% = 98,36%
Referensi
- Canavos, g. 1988. Probabilitas dan Statistik: Aplikasi dan Metode. Bukit McGraw.
- Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
- Levin, r. 1988. Statistik untuk administrator. 2nd. Edisi. Prentice Hall.
- Sudman, s.1982. Mengajukan pertanyaan: Panduan praktis untuk desain kuesioner. San Fransisco. Jossey Bass.
- Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.
- Wonnacott, t.H. dan r.J. Wonnacott. 1990. Statistik pengantar. Edisi ke -5. Wiley
- Wikipedia. Kesalahan sampel. Diperoleh dari: di.Wikipedia.com
- Wikipedia. Margin kesalahan. Diperoleh dari: di.Wikipedia.com
- « Sejarah statistik inferensial, karakteristik, untuk apa, contohnya
- U -test dari Mann - Whitney Apa dan ketika berlaku, eksekusi, contoh »

