Evaluasi fungsi

Untuk mengevaluasi fungsi diagram yang diketahui, untuk nilai atau elemen tertentu dari set awal, itu cukup untuk mengamati elemen yang sesuai dalam set kedatangan. Sumber: f. Zapata.

Apa evaluasi fungsi?

Itu Evaluasi fungsi Itu terdiri dalam menentukan gambar nilai domain tertentu. Dengan kata lain, untuk nilai yang diberikan dari set awal, Anda harus menemukan yang sesuai di set kedatangan.

Suatu fungsi dapat diwakili dalam beberapa cara. Jika, misalnya, diagram Venn tersedia, evaluasi ini sangat sederhana, cukup untuk memilih elemen set awal atau domain, dan melihat elemen yang sesuai dengan set kedatangan.

Dalam "…… adalah diagram modal ...", diwakili di atas, ketika mengevaluasi fungsi ini dalam elemen "Kanada", itu adalah elemen "Ottawa", jika terjadi dengan "Meksiko", itu adalah "Kota Meksiko" dan dan segera.

Jika fungsi diberikan dalam bentuk pasangan rapi, evaluasi juga sederhana: anggota kedua dari torsi tertib adalah gambar anggota pertama. Misalnya, dengan fungsi f (x) yang dijelaskan oleh:

f (x) = (0.0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Saat mengevaluasi fungsi untuk nilai 3, hasilnya adalah 6; Saat mengevaluasi untuk 5, itu adalah 10 dan seterusnya.

Demikian juga, suatu fungsi dapat dievaluasi saat grafik tersedia, asalkan nilai yang ingin Anda evaluasi muncul di dalamnya.

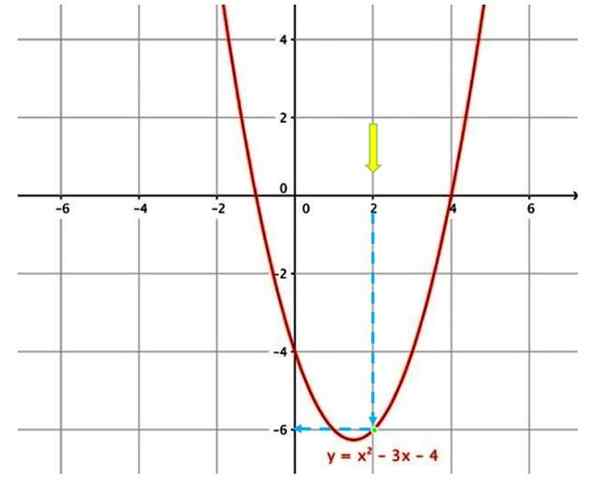Grafik untuk mengevaluasi suatu fungsi

Misalnya, untuk mengevaluasi fungsi yang ditunjukkan di atas, pada x = 2, hal pertama adalah menemukan dalam grafik a x = 2 (panah kuning).

Kemudian, Anda harus bergerak mengikuti panah vertikal biru, sampai Anda menyentuh kurva (titik hijau). Ikuti panah biru lagi, yang menunjukkan nilai yang sesuai pada sumbu vertikal, oleh karena itu, ketika mengevaluasi fungsi pada x = 2, y = −6 diperoleh.

Ini dapat melayani Anda: Fungsi Trigonometri: Dasar, di bidang Cartesian, Contoh, Latihan

Mengevaluasi fungsi yang diberikan dalam notasi matematika

Di bagian bawah grafik di atas, fungsi grafik muncul, tetapi diberikan dalam notasi matematika, yaitu, melalui rumus:

f (x) = x² - 3x - 4

Ketika Anda ingin mengevaluasi fungsi dalam nilai apa pun x = a, Anda harus menemukan f (a), yang hanya dibaca "f dari a".

Untuk menemukan hasilnya, x = a diganti dalam rumus fungsi, dan operasi dan perhitungan yang diminta dilakukan di sana.

Misalkan Anda ingin mengevaluasi fungsi contoh pada x = −1. Ini berarti bahwa f (−1) harus ditemukan.

Langkah pertama adalah mengganti x = -1 di fungsi:

f (−1) = (−1)² - 3 ∙ (−1) - 4

Dan kemudian, lakukan operasi yang ditunjukkan, yang dalam contoh ini adalah:

• Temukan kuadrat −1: (−1)² = 1
• Kurangi nilai sebelumnya dari produk 3 ∙ (−1): 3 ∙ (−1) = −3
• Dari hasil sebelumnya, kurangi 4

f (−1) = (−1)² - 3 ∙ (−1) - 4 = 1 + 3 - 4 = 0

Pembaca dapat menguatkan hasil ini, dari grafik fungsi.

Prosedur yang dijelaskan dapat digunakan untuk mengevaluasi fungsi pada nilai domain lainnya. Misalnya, Anda dapat menemukan f (-2), f (100) atau bahkan f (h), di mana h adalah nilai variabel sewenang-wenang, yang termasuk dalam domain fungsi.

Mengevaluasi fungsi pada nilai x = h 

Misalkan Anda ingin mengevaluasi fungsi pada beberapa nilai sewenang -wenang, sering operasi dalam perhitungan matematika.

Dalam hal ini, X digantikan oleh H, dengan cara yang sama seperti yang dilakukan ketika X mengambil nilai numerik, dan hasilnya disederhanakan sebanyak mungkin.

Ketika operasi yang dihasilkan tidak dapat lagi disederhanakan, operasi yang dihasilkan tersisa.

Itu dapat melayani Anda: enegon: properti, cara membuat enegon, contoh

Contoh

Anda ingin mengevaluasi fungsi f (x) = x² - 3x - 4 at x = h+1. Pendekatan yang diperlukan adalah sebagai berikut:

f (h+1) = (h+1)² - 3 ∙ (h+1) - 4

Di sebelah kanan kesetaraan, istilah pertama adalah produk yang luar biasa:

(H+1)² = h² +2H + 1

Istilah berikut diselesaikan melalui properti distributif:

3 ∙ (h + 1) = 3H + 3

Saat mengganti semua hal di atas, Anda memiliki:

f (h+1) = (h+1)² - 3 ∙ (h+1) - 4 = h² +2H + 1 - (3H + 3) - 4

Istilah serupa dikurangi, dengan jumlah aljabar:

f (h+1) = h² + 2H + 1 - 3H - 3 - 4 = h² - H - 6

Hasil bagi diferensial

Kreasien diferensial atau rasio perbedaan D dari suatu fungsi f (x) didefinisikan sebagai:

Dengan kondisi h ≠ 0, yang diperlukan, karena pembagian dengan 0 tidak didefinisikan.

Hasil bagi ini ditafsirkan secara geometris sebagai kemiringan garis penjelasan ke kurva, yaitu garis yang melewati dua titik. Koordinat poin -poin ini adalah: [x, f (x)] dan [x+h; f (x+h)], seperti yang terlihat pada gambar berikut:

Kreasien diferensial setara dengan menghitung kemiringan garis penjahitan ke kurva, yang melewati titik -titik yang ditunjukkan. Sumber: Wikimedia Commons.

Itulah sebabnya hasil bagi ini muncul dalam perhitungan turunan dari suatu fungsi, karena membuat "h" mendekati nilai 0, garis sekte cenderung menjadi garis singgung pada titik (x, y), karena titik -titik di persimpangan dari Angka itu sangat dekat sehingga mereka cenderung ke titik yang sama.

Dengan demikian, garis menjadi garis singgung (mencegat kurva dalam satu titik).

Ini justru definisi yang berasal dari suatu fungsi: kemiringan garis garis singgung ke kurva di titik koordinat (x, f (x)))).

Itu dapat melayani Anda: media tertimbang: bagaimana itu dihitung, contoh dan latihan

Seperti dapat dilihat, hasil bagi diferensial membutuhkan evaluasi fungsi dalam (x + h) dan di x. Contoh -contoh berikut menggambarkan cara melakukannya.

Contoh 1

Anda ingin menemukan hasil bagi dari fungsi f (x) = 2x - 3. Langkah pertama adalah meningkatkan evaluasi fungsi untuk x = x + h, seperti ini:

f (x+h) = 2 ∙ (x+h) - 3 = 2x+2h - 3

Kemudian, hasilnya diganti dalam definisi D, yang diberikan sebelumnya:

Dengan h ≠ 0.

Pembilang disederhanakan sejauh mungkin, mengurangi istilah yang sama:

Akhirnya, faktor umum dalam pembilang dan penyebut disederhanakan:

D = 2

Contoh 2

Temukan hasil bagi diferensial fungsi f (x) = x² - 3x - 4.

Kami melanjutkan seperti pada contoh sebelumnya, menemukan F (x+h) pertama, mengganti hasil di D dan menyederhanakan maksimum:

f (x+h) = (x+h)² - 3 (x+h) - 4 = x² + 2hx + h² - 3x - 3H - 4

= 2x+H-3

Karena itu:

D = 2x+H-3

Dimana h ≠ 0.

Latihan terpecahkan

Latihan 1

Mengevaluasi fungsi f (x) = 2x² - 4x + 1 Kapan:

a) x = -1
b) x = 0
c) x = 2

Solusi untuk

F (-1) = 2 (-1)² - 4 (-1) + 1 = 2 + 4 + 1 = 7

Solusi b

f (0) = 2 (0)² - 4 (0) + 1 = 0 - 0 + 1 = 1

Solusi c

f (2) = 2 ∙ 2² - 4 ∙ 2 + 1 = 8 - 8 + 1 = 1

Latihan 2

Tim konservasionis menentukan bahwa fungsi w (t) = 0.LT² + 1.8t berfungsi untuk memodelkan jumlah limbah "w", dalam kilogram, yang dilemparkan ke sungai tertentu, dalam waktu "t", diberikan dalam beberapa hari.

Hitung jumlah limbah yang dilemparkan ke sungai di akhir:

a) 3 hari
b) 1 minggu
c) 1 bulan

Solusi untuk

W (t) Fungsi dievaluasi pada t = 3 hari:

W (3) = 0.1 × 3² +1.8 × 3 = 0.9 + 5.4 = 6.3 kilogram

Solusi b

Sebelum mengevaluasi, Anda harus menghabiskan 1 minggu ke hari:

1 minggu = 7 hari

W (7) = 0.1 × 7² +1.8 × 7 = 4.9 + 12.6 = 17.5 kilogram

Solusi c

Sekali lagi, perlu mengubah berbulan -bulan menjadi hari:

1 bulan = 30 hari

W (30) = 0.1 × 30² +1.8 × 30 = 90 + 54 = 144 kilogram

Referensi

1. Larson, r. 2012. Prekalkulasi. Ke -8. Edisi. Pembelajaran Cengage.
2. Institut Monterey. Mengevaluasi fungsi. Pulih dari: montereyinstitute.org.
3. Stewart, J. 2007. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
4. Sullivan, m. 1997. Prekalkulasi. 4. Edisi. Pendidikan Pearson.
5. Zill, d. 2008. Prekcculment dengan kemajuan perhitungan. 4. Edisi. Bukit McGraw.