Apakah ada segitiga scalene dengan sudut kanan?

Ada banyak segitiga scalele dengan sudut kanan. Sebelum memajukan masalah ini, pertama -tama perlu mengetahui berbagai jenis segitiga yang ada. Segitiga diklasifikasikan oleh dua kelas yaitu: sudut internal mereka dan panjang sisi mereka.

Jumlah sudut internal segitiga selalu sama dengan 180º. Tetapi menurut langkah sudut internal diklasifikasikan sebagai:

-Acutangle: Segitiga itu sedemikian rupa sehingga tiga sudutnya akut, yaitu, masing -masing kurang dari 90 °.

-Persegi panjang: Mereka adalah segitiga yang memiliki sudut kanan, yaitu, sudut yang berukuran 90 °, dan, oleh karena itu, dua sudut lainnya akut.

-Tumpul: Mereka adalah segitiga yang memiliki sudut tumpul, yaitu sudut yang ukurannya lebih besar dari 90 °.

Segitiga scalan dengan sudut kanan

Minat pada bagian ini adalah untuk menentukan apakah segitiga scalene dapat memiliki sudut kanan.

Seperti yang dikatakan di atas, sudut kanan adalah sudut yang ukurannya 90º. Hanya perlu mengetahui definisi segitiga scalene, yang tergantung pada panjang sisi segitiga.

Klasifikasi segitiga menurut sisi mereka

Menurut panjang sisi mereka, segitiga diklasifikasikan sebagai:

-Sama sisi: Mereka semua segitiga itu sedemikian rupa sehingga panjang ketiga sisi mereka adalah sama.

-Sama kaki: Mereka adalah segitiga yang memiliki dua sisi dengan panjang yang sama.

-Sisi tak sama panjang: Mereka adalah segitiga di mana ketiga sisi memiliki langkah yang berbeda.

Formulasi pertanyaan yang setara

Pertanyaan yang setara dengan judulnya adalah “Apakah ada segitiga yang memiliki ketiga sisi dengan langkah -langkah yang berbeda dan ini memiliki sudut 90 °?"

Jawaban yang dinyatakan di awal adalah ya. Tidak terlalu sulit untuk membenarkan jawaban ini.

Jika diamati dengan hati -hati, tidak ada segitiga persegi panjang yang sama -sama, ini dapat dibenarkan berkat teorema Pythagoras untuk segitiga persegi panjang, yang mengatakan:

Diberi segitiga persegi panjang bahwa panjang kategorinya adalah "A" dan "B", dan panjangnya yang dihipoten adalah "C", Anda harus C² = A²+B², yang dapat dilihat bahwa panjang hipotenuse " C "selalu lebih besar dari panjang setiap kaki.

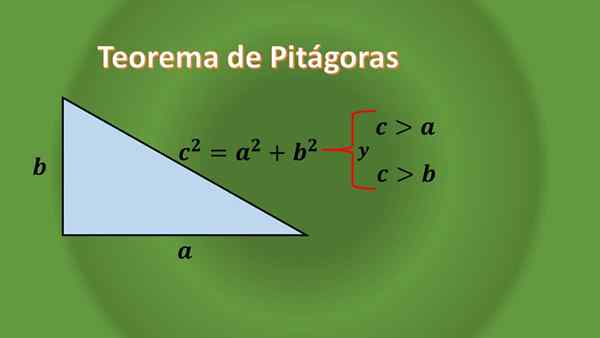
Karena tidak ada yang dikatakan tentang "A" dan "B", maka ini menyiratkan bahwa segitiga siku -siku dapat menjadi sama sekali atau skalene.

Kemudian, cukup pilih segitiga persegi panjang sehingga kakinya memiliki ukuran yang berbeda, dan dengan demikian segitiga scalene yang memiliki sudut kanan akan dipilih.

Contoh

-Jika segitiga persegi panjang dipertimbangkan yang kakinya memiliki panjang masing -masing 3 dan 4, maka oleh teorema Pythagoras dapat disimpulkan bahwa hipotenus akan memiliki panjang 5. Ini menyiratkan bahwa segitiga adalah scalene dan memiliki sudut kanan.

-Biarkan ABC menjadi segitiga persegi panjang dengan ukuran pengukuran 1 dan 2. Maka panjangnya hipotenus adalah √5, yang menyimpulkan bahwa ABC adalah segitiga persegi panjang skalene.

Tidak setiap segitiga skala memiliki sudut yang tepat. Anda dapat mempertimbangkan segitiga seperti gambar berikut, yaitu skalene, tetapi tidak ada sudut internalnya yang lurus.

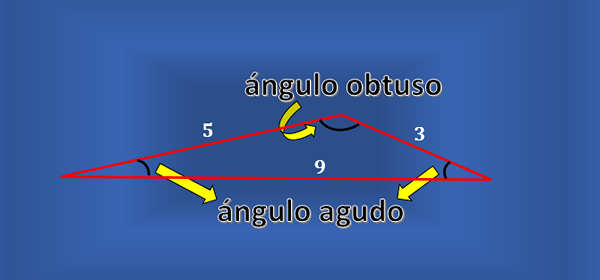Selain itu, tidak setiap segitiga kanan adalah Scalene. Jika Anda mempertimbangkan segitiga siku -siku yang kakinya mengukur keduanya, maka hipotenus akan memiliki ukuran √2. Oleh karena itu, segitiga persegi panjang adalah Isosceles.