Anjak

Apa faktorisasi?

Faktorisasi adalah metode yang melaluinya polinomial dinyatakan dalam bentuk multiplikasi faktor, yang dapat berupa angka, huruf atau keduanya. Untuk memperhitungkan, faktor -faktor yang umum untuk istilah dikelompokkan, dan dengan cara ini polinomial didekomposisi dalam beberapa polinomial.

Jadi, ketika faktor bertambah satu sama lain hasilnya adalah polinomial asli. Faktorisasi adalah metode yang sangat berguna ketika ada ekspresi aljabar, karena dapat menjadi multiplikasi dari beberapa istilah sederhana; Misalnya: 2nd² + 2ab = 2a _* (A + B).

Ada kasus -kasus di mana polinomial tidak dapat dimasukkan karena tidak ada faktor umum di antara persyaratannya; Dengan demikian, ekspresi aljabar ini hanya dapat dibagi antara mereka dan dengan 1. Misalnya: x + y + z.

Dalam ekspresi aljabar, faktor umum adalah pembagi umum maksimum dari istilah yang menyusunnya.

Metode faktorisasi

Ada beberapa metode faktorisasi, yang diterapkan tergantung pada kasusnya. Beberapa di antaranya adalah sebagai berikut:

Faktorisasi umum

Dalam metode ini faktor -faktor yang umum diidentifikasi; yaitu, mereka yang diulang dalam hal ekspresi. Kemudian properti distributif diterapkan, pembagi umum maksimum dihapus dan faktorisasi selesai.

Dengan kata lain, faktor umum dari ekspresi diidentifikasi dan setiap istilah dibagi antara ini; Istilah yang dihasilkan akan dikalikan dengan pembagi umum maksimum untuk mengekspresikan faktorisasi.

Contoh 1

Faktorisasi (b²x) + (b²Dan).

Larutan

Pertama adalah faktor umum dari setiap istilah, yang dalam hal ini b², Dan kemudian istilah dibagi antara faktor umum sebagai berikut:

(B²x) / b² = x

(B²y) / b² = y.

Faktorisasi dinyatakan, mengalikan faktor umum dengan istilah yang dihasilkan:

(B²x) + (b²y) = b² (x + y).

Contoh 2

Faktorisasi (ke -2²B³) + (3ab²).

Larutan

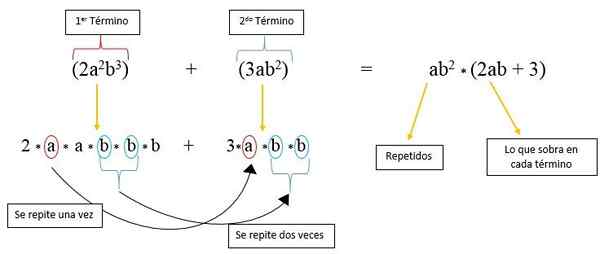
Dalam hal ini kami memiliki dua faktor yang diulang dalam setiap istilah yang "A" dan "B", dan yang dinaikkan menjadi kekuatan. Untuk memperhitungkan mereka terlebih dahulu, kedua istilah itu dipecah dalam bentuk panjangnya:

2_*ke_*ke_*B_*B_*B + 3A_*B_*B

Dapat dilihat bahwa faktor "A" diulangi hanya sekali dalam semester kedua, dan faktor "B" diulangi dua kali dalam hal ini; Jadi dalam istilah pertama hanya ada 2, faktor "a" dan satu "b"; Sedangkan dalam istilah kedua hanya 3 tersisa.

Oleh karena itu, ditulis sebanyak "A" dan "B" diulang dan dikalikan dengan faktor -faktor yang tersisa dari setiap istilah, seperti yang diamati pada gambar:

Faktorisasi pengelompokan

Karena tidak dalam semua kasus pembagi umum maksimum polinomial diungkapkan dengan jelas, perlu membuat langkah -langkah lain untuk dapat menulis ulang polinomial dan dengan demikian membuat faktorisasi.

Dapat melayani Anda: bagian kerucut: jenis, aplikasi, contoh

Salah satu langkah itu adalah mengelompokkan ketentuan polinomial ke dalam beberapa kelompok, dan kemudian menggunakan metode faktor umum.

Contoh 1

Faktorisasi AC + BC + AD + BD.

Larutan

Ada 4 faktor di mana dua adalah umum: dalam istilah pertama itu adalah "c" dan di kedua itu adalah "d". Dengan begitu kedua istilah tersebut dikelompokkan dan terpisah:

(Ac + bc) + (ad + bd).

Sekarang dimungkinkan untuk menerapkan metode faktor umum, membagi setiap istilah dengan faktor umum dan kemudian mengalikan faktor umum dengan istilah yang dihasilkan, seperti ini:

(Ac + bc) / c = a + b

(iklan + bd) / d = a + b

C (A + B) + D (A + B).

Sekarang binomial diperoleh yang umum untuk kedua istilah. Untuk memperhitungkannya dikalikan dengan faktor -faktor yang tersisa; Dengan begitu Anda harus:

AC + BC + AD + BD =  (C + D) _* (A + B).

Faktorisasi inspeksi

Metode ini digunakan untuk memperhitungkan polinomial kuadratik, juga disebut trinomial; yaitu mereka yang terstruktur sebagai kapak² ± BX + C, di mana nilai "A" berbeda dari 1. Metode ini juga digunakan saat trinomial memiliki bentuk x² ± BX + C dan nilai "A" = 1.

Contoh 1

Faktor X² + 5x + 6.

Larutan

Anda memiliki trinomial kuadratik dari bentuk x² ± bx + c. Untuk memperhitungkannya terlebih dahulu, dua angka harus ditemukan bahwa, ketika mengalikan, menghasilkan nilai "C" (yaitu, 6) dan bahwa jumlahnya sama dengan koeffik "B". Angka -angka itu adalah 2 dan 3:

2 _* 3 = 6

2 + 3 = 5.

Dengan cara ini, ekspresi disederhanakan sebagai berikut:

(X² + 2x) + (3x + 6)

Setiap istilah adalah faktor:

• Untuk (x² + 2x) Istilah umum dihapus: x (x + 2)
• Untuk (3x + 6) = 3 (x + 2)

Dengan demikian, ekspresi tetap:

x (x +2) +3 (x +2).

Karena Anda memiliki binomial yang umum, untuk mengurangi ekspresi, ia melipatgandakan ini dengan istilah sisa dan harus:

X² + 5x + 6 = (x + 2) _* (x + 3).

Contoh 2

Faktorisasi 4A² + 12a +9 = 0.

Larutan

Anda memiliki trinomial kuadratik dari bentuk kapak² ± BX + C dan untuk memperhitungkannya melipatgandakan semua ekspresi dengan koefisien x²; Dalam hal ini, 4.

4² + 12a +9 = 0

4² (4) + 12a (4) + 9 (4) = 0 (4)

16 a² + 12a (4) + 36 = 0

4² ke² + 12a (4) + 36 = 0

Sekarang dua angka harus ditemukan bahwa, ketika bertambah satu sama lain, menghasilkan nilai "C" (yaitu 36) dan bahwa ketika bergabung dengan koefisien istilah "A", yaitu 6.

6 _* 6 = 36

6 + 6 = 12.

Dengan begitu ekspresi ditulis ulang, dengan mempertimbangkan 4 bahwa 4² ke² = 4a _* 4. Oleh karena itu, properti distributif diterapkan untuk setiap istilah:

Dapat melayani Anda: kotak mackinder

(4a + 6) _* (4a + 6).

Akhirnya, ekspresi dibagi dengan koefisien a²; yaitu, 4:

(4a + 6) _* (4a + 6) / 4 = ((4a + 6) / 2) _* ((4a + 6)/ 2).

Ekspresinya adalah sebagai berikut:

4² + 12a +9 = (2a +3) _* (2a + 3).

Faktorisasi dengan produk terkenal

Ada kasus di mana, untuk sepenuhnya memperhitungkan polinomial dengan metode sebelumnya, itu menjadi proses yang sangat panjang.

Itulah sebabnya ekspresi dapat dikembangkan dengan formula produk terkenal dan dengan demikian prosesnya menjadi lebih sederhana. Di antara produk terkenal yang paling banyak digunakan adalah:

• Perbedaan dua kotak: (a² - B²) = (a - b) _* (A + B)
• Kuadrat sempurna dari jumlah: a² + 2ab +b² = (a + b)²
• Perfect Square of a Difference: a² - 2ab + b² = (a - b)²
• Perbedaan dua kubus: a³ - B³ = (a-b)_*(ke² + ab + b²)
• Jumlah dua kubus: a³ - B³ = (a + b) _* (ke² - ab + b²)

Contoh 1

Faktorisasi (5² - X²)

Larutan

Dalam hal ini ada perbedaan dua kotak; Oleh karena itu, formula produk terkenal diterapkan:

(ke² - B²) = (a - b) _* (A + B)

(5² - X²) = (5 - x) _* (5 + x)

Contoh 2

Faktorisasi 16x² + 40x + 25²

Larutan

Dalam hal ini, ada kuadrat sempurna dari jumlah, karena dua istilah persegi dapat diidentifikasi, dan istilah yang tersisa adalah hasil dari pengalikan dua dengan akar kuadrat dari istilah pertama, dengan akar kuadrat dari istilah kedua.

ke² + 2ab +b² = (a + b)²

Untuk memperhitungkan, hanya akar kuadrat dari istilah pertama dan ketiga yang dihitung:

√ (16x²) = 4x

√ (25²) = 5.

Kemudian dua istilah yang dihasilkan dinyatakan dipisahkan oleh tanda operasi, dan semua polinomial kuadrat meningkat:

16x² + 40x + 25² = (4x + 5)².

Contoh 3

Faktorisasi 27a³ - B³

Larutan

Ekspresi mewakili pengurangan di mana dua faktor meningkat ke kubus. Untuk memperhitungkan mereka, formula produk terkenal dari perbedaan kubus diterapkan, yaitu:

ke³ - B³ = (a-b)_*(ke² + ab + b²)

Dengan demikian, untuk memperhitungkan, akar kubik dihilangkan dari setiap istilah binomial dan dikalikan dengan kuadrat dari istilah pertama, ditambah produk yang pertama dengan istilah kedua, ditambah istilah kedua kuadrat.

27a³ - B³

³√ (27a³) = 3a

³√ (-b³) = -b

27a³ - B³ = (3a - b) _* [(3a)² + 3ab + b²)]

27a³ - B³ = (3a - b) _* (9a² + 3ab + b²)

Faktorisasi dengan aturan ruffini

Metode ini digunakan ketika Anda memiliki polinomial derajat lebih dari dua, untuk menyederhanakan ekspresi ke beberapa polinomial yang lebih kecil.

Contoh 1

Factorice q (x) = x⁴ - 9x² + 4x + 12

Larutan

Pertama angka -angka yang merupakan pembagi dari 12 dicari, yang merupakan istilah independen; Ini adalah ± 1, ± 2, ± 3, ± 4, ± 6 dan ± 12.

Dapat melayani Anda: kelipatan 2: apa itu dan penjelasan

Maka x digantikan oleh nilai -nilai ini, dari yang paling sedikit ke terbesar, dan karenanya ditentukan dengan nilai -nilai yang akan tepat divisi; Artinya, sisanya harus 0:

x = -1

Q (-1) = (-1)⁴ - 9 (-1)² + 4 (-1) + 12 = 0.

x = 1

Q (1) = 1⁴ - 9 (1)² + 4 (1) + 12 = 8 ≠ 0.

x = 2

Q (2) = 2⁴ - 9 (2)² + 4 (2) + 12 = 0.

Dan seterusnya untuk setiap pembagi. Dalam hal ini, faktor -faktor yang ditemukan adalah untuk x = -1 dan x = 2.

Metode ruffini sekarang diterapkan, yang menurutnya koefisien ekspresi akan dibagi dengan faktor -faktor yang ditemukan sehingga pembagian itu tepat. Istilah polinomial dipesan dari eksponen yang lebih besar ke lebih rendah; Dalam hal istilah tidak ada dengan tingkat yang mengikuti dalam urutan, 0 ditempatkan di tempatnya.

Koefisien terletak dalam skema seperti yang terlihat pada gambar berikut.

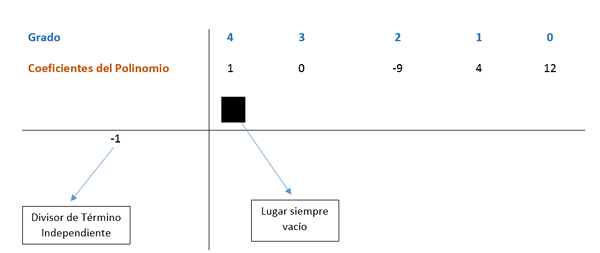
Koefisien pertama diturunkan dan dikalikan dengan pembagi. Dalam hal ini, pembagi pertama adalah -1, dan hasilnya ditempatkan di kolom berikut. Maka nilai koefisien dengan hasil yang diperoleh ditambahkan secara vertikal dan hasilnya ditempatkan di bawah. Dengan begitu prosesnya diulangi sampai kolom terakhir.

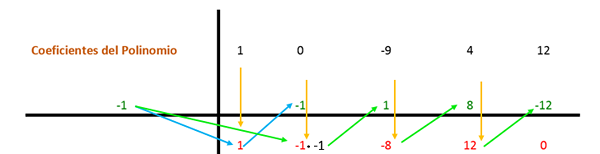
Maka prosedur yang sama diulang lagi, tetapi dengan pembagi kedua (yaitu 2) karena ekspresi masih dapat disederhanakan.

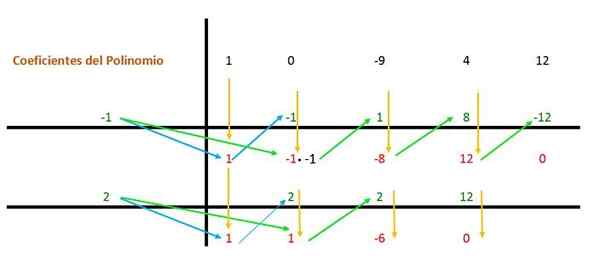
Dengan demikian, untuk setiap root dicapai, polinomial akan memiliki istilah (x - a), di mana "a" adalah nilai root:

(x - (-1)) _* (x - 2) = (x + 1) _* (x - 2)

Di sisi lain, istilah -istilah ini harus dikalikan dengan sisanya yang tetap dari aturan Ruffini 1: 1 dan -6, yang merupakan faktor yang mewakili gelar. Dengan cara ini bentuk ekspresi adalah: (x² + X - 6).

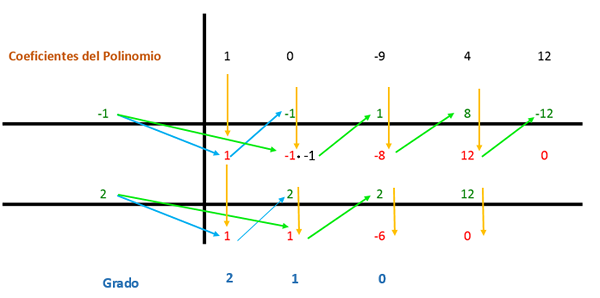
Memperoleh hasil faktorisasi polinomial dengan metode Ruffini adalah:

X⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2) _* (X² + X - 6)

Akhirnya, polinomial grade 2 yang muncul dalam ekspresi sebelumnya dapat ditulis ulang sebagai (x+3) (x-2). Oleh karena itu, faktorisasi terakhir adalah:

X⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2)_*(x+3)_*(X-2).

Referensi

1. Arthur Goodman, L. H. (seribu sembilan ratus sembilan puluh enam). Aljabar dan trigonometri dengan geometri analitik. Pendidikan Pearson.
2. J, v. (2014). Bagaimana mengajar anak -anak tentang anjak polinomial.
3. Manuel Morillo, a. S. (S.F.). Matematika dasar dengan aplikasi.
4. Roelse, hlm. L. (1997). Metode linier untuk faktorisasi polinomial di atas bidang terbatas: teori dan implementasi. Universitas Essen.
5. Sharpe, d. (1987). Cincin dan faktorisasi.