Aliran medan listrik

Apa itu aliran medan listrik?

Dia Aliran medan listrik atau hanya aliran listrik adalah kuantitas skalar sebanding dengan jumlah saluran medan listrik yang melintasi permukaan. Itu dilambangkan dengan huruf kapital modal φ (phi).

Medan listrik tidak benar -benar "mengalir" seperti aliran air, meskipun garis aliran fluida menyerupai lereng dari medan listrik.

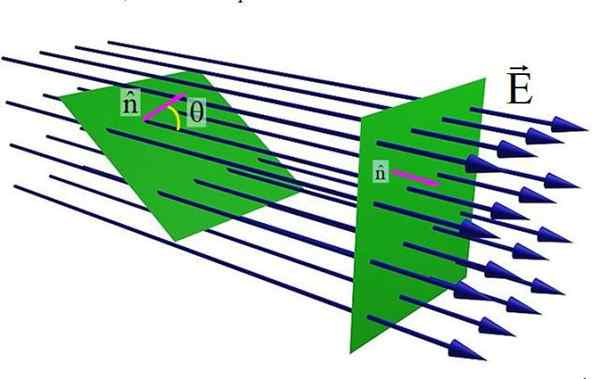
Gambar 1. Aliran medan listrik melalui permukaan datar. Sumber: Wikimedia Commons.

Gambar atas menunjukkan permukaan datar yang dilintasi oleh medan listrik DAN. Saat vektor unit normal ke permukaan N dan lapangan DAN Mereka paralel, jumlah garis bidang yang melintasi permukaan maksimal. Tetapi ketika sudut θ meningkat antara N Dan DAN, Jumlah garis yang melewati permukaan hijau lebih rendah.

Di sisi lain, aliran medan listrik juga tergantung pada besarnya DAN, Karena semakin tinggi ini, semakin banyak garis medan mereka melintasi permukaan. Dan tentu saja, semakin besar area S permukaan tersebut, juga aliran, sehingga persamaan berikut ditetapkan:

Φ = e ∙ sosθ

Ekspresi ini konsisten dengan produk skalar di antara vektor DAN Dan N:

Φ = (DAN • N) S

Unit untuk aliran medan listrik dalam sistem unit internasional jika n.M²/C (Newton x Square Metro/Coulomb). Atau, karena bidang ini juga diukur dalam V/M (volt di kereta bawah tanah), aliran listrik dalam (v ∙ m) m).

Contoh

Menurut definisi, aliran listrik bisa positif, negatif atau sama dengan 0. Aliran medan listrik adalah:

Itu dapat melayani Anda: magnetisasi: momen magnetik orbital dan putaran, contoh

-Positif saat sudut θ DAN Dan N Kurang dari 90º, karena cos θ lebih besar dari nol.

-Negatif jika sudut ini lebih besar dari 90º, karena cos θ kurang dari nol.

-Batal saat θ bernilai tepat 90º, karena cos 90º = 0 dan garis bidang dalam kasus ini tangensial ke permukaan.

-Di sisi lain, jika sudut di antara DAN Dan N Itu sama dengan 0, aliran memperoleh nilai maksimumnya.

Kemungkinan -kemungkinan ini ditunjukkan pada gambar berikut:

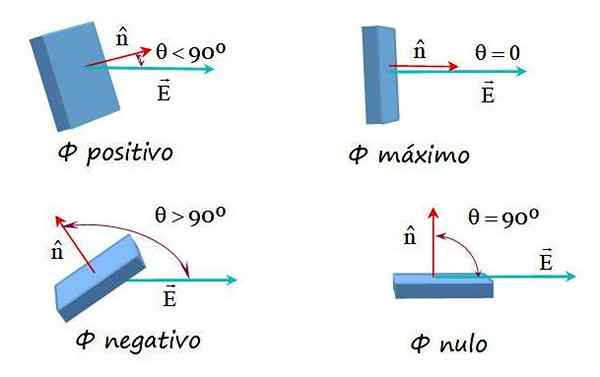Gambar 2. Contoh aliran medan listrik dengan berbagai orientasi antara bidang dan vektor permukaan normal. Sumber: f. Zapata.

Aliran medan listrik pada permukaan sewenang -wenang

Sebelumnya aliran medan listrik ditentukan dalam kasus tertentu dari bidang seragam yang mempengaruhi permukaan datar. Untuk permukaan sewenang -wenang dan/atau medan listrik non -uniform, sudut antara DAN Dan N dapat bervariasi dari titik ke titik.

Pada gambar berikut ada dua contoh, di sebelah kiri permukaan melengkung dan di sebelah kanan permukaan tertutup.

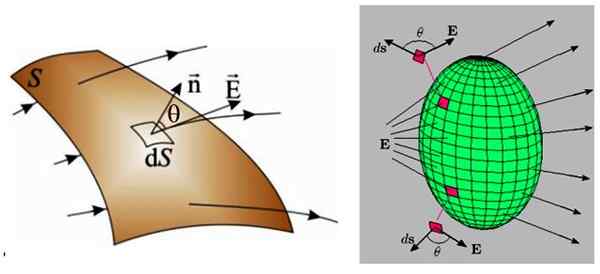Gambar 3. Di sebelah kiri permukaan sewenang -wenang yang melaluinya medan listrik non -uniform melintasi. Di sebelah kanan medan listrik non -uniform melintasi permukaan tertutup, oleh karena itu aliran bersih dalam kasus itu batal. Sumber: f. Zapata.

Dalam kedua kasus, permukaan dibagi menjadi beberapa daerah yang jauh lebih kecil, dengan ukuran yang sangat kecil, yang disebut DS, yang juga melintasi aliran Infinitesimal Dφ:

dφ = (DAN•N) Ds = (ecosθ) ds

Total bidang diperoleh dengan menambahkan semua kontribusi yang sangat kecil ini:

Simbol S sebagai subskrip dalam integral menunjukkan bahwa itu harus dihitung di seluruh permukaan. Jika ini ditutup, dilambangkan dengan lingkaran kecil di integral:

Dapat melayani Anda: Konstanta Antoine: Rumus, Persamaan, Contoh

Dalam hal permukaan tertutup, N Selalu tunjukkan, jadi alirannya memiliki tanda + saat keluar, karena sudut antara DAN Dan N kurang dari 90º, dan tanda - saat lapangan masuk, karena sudut antara DAN Dan N lebih besar dari 90º (lihat Gambar 2).

Perhatikan bahwa pada permukaan tertutup di sebelah kanan, jumlah garis medan yang memasuki permukaan sama dengan jumlah garis yang keluar. Oleh karena itu aliran bersih, didefinisikan sebagai jumlah aljabar dari aliran yang masuk dan aliran keluar, batal.

Sumber medan listrik dalam kasus ini berada di luar permukaan, namun, aliran bersih akan berbeda dari 0 jika sumber medan listrik (distribusi beban) berada di dalam permukaan.

Latihan

Latihan 1

Anda memiliki medan listrik DAN = 3.5 kn/c X dan permukaan persegi panjang datar 0.Lebar 35 m oleh 0.Panjang 7 m. Temukan aliran medan listrik yang melintasi persegi panjang dalam kasus -kasus berikut:

a) Permukaan sejajar dengan bidang YZ.

b) Persegi panjang sejajar dengan bidang XY.

c) bidang normal membentuk sudut 40º dengan sumbu x dan mengandung sumbu dan.

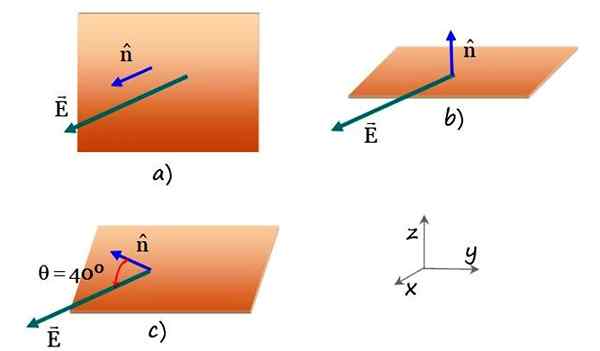Gambar 4. Bidang persegi panjang yang disilangkan oleh medan listrik yang seragam dalam orientasi bidang yang berbeda. Sumber: f. Zapata.

Solusi untuk

Vektor normal dan vektor medan listrik paralel, oleh karena itu sudut θ antara keduanya adalah 0º dan aliran listrik adalah:

Φ = (e ∙ s) cos 0 = e ∙ s

Area S persegi panjang adalah:

Dapat melayani Anda: Metode jajaran genjang: contoh, latihan terpecahkan

S = 0.35 m x 0.7 m = 0.245 m²

Mengganti φ:

Φ = E ∙ S = 3.5 x 10³ N/c × 0.245 m² = 857.5 n ∙ m² /C.

Solusi b

Aliran medan listrik adalah 0, karena vektor DAN Dan N Mereka saling tegak lurus.

Solusi c

Sudut θ antara bidang DAN dan vektor normal N adalah 40º (lihat gambar), oleh karena itu:

Φ = e ∙ s ∙ cos θ = 3.5 x 10³ N/c × 0.245 m² × cos 40º = 656.9 n ∙ m² /C.

Latihan 2

Hitung aliran medan listrik yang menghasilkan beban tepat waktu positif itu_{salah satu} = 2μC terletak di tengah sphere jari -jari r = 5 cm.

Larutan

Bidang yang diproduksi oleh beban q_{salah satu} Ini bukan seragam, tetapi dari hukum Coulomb diketahui bahwa di permukaan bola, ia memiliki besarnya:

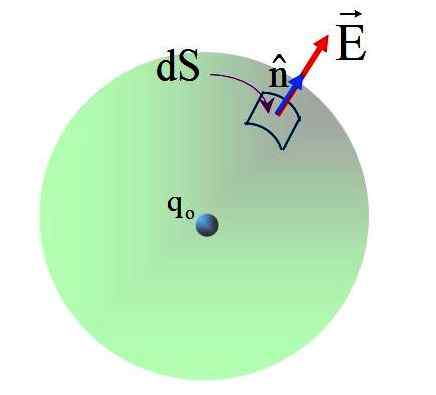Gambar 5. Lalat bidang yang diproduksi di permukaan bola dengan beban tepat waktu di tengahnya. Sumber: f. Zapata.

Lapangan memiliki arah radial, dan vektor normal N, Oleh karena itu sudut antara kedua vektor adalah 0 di semua titik permukaan bola. Mengganti:

Kamu harus:

Integral DS di seluruh permukaan bola S adalah luasnya, yaitu 4πr^2, Karena itu:

Yang menyimpulkan bahwa aliran medan listrik tidak tergantung pada permukaan S, tetapi pada beban terkunci di dalamnya.

Nilainya adalah:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m²/C = 2.3 x 10⁵ N⋅m²/C

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
2. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 5. Elektrostatika. Diedit oleh Douglas Figueroa (USB).
3. Giambattista, a. 2010. Fisika. 2nd. Ed. Bukit McGraw.
4. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1. Pearson.