Rumus frekuensi akumulasi, perhitungan, distribusi, contoh

Itu frekuensi akumulasi Itu adalah jumlah frekuensi absolut f, dari anak yang sesuai dengan nilai variabel tertentu. Pada gilirannya, frekuensi absolut adalah berapa kali pengamatan muncul dalam set data.

Jelas, variabel studi harus tertib. Dan karena frekuensi akumulasi diperoleh dengan menambahkan frekuensi absolut, ternyata frekuensi akumulasi ke data terakhir harus bertepatan dengan jumlah total dari mereka. Jika tidak ada kesalahan dalam perhitungan.

Frekuensi akumulasi digunakan dalam pengelolaan data statistik

Secara umum, frekuensi akumulasi dilambangkan sebagai f_yo (Atau terkadang n_yo), untuk membedakannya dari frekuensi absolut f_yo dan penting untuk menambahkan kolom untuk itu dalam tabel dengan mana data diatur, dikenal sebagai Tabel frekuensi.

Dengan cara ini difasilitasi, antara lain, untuk menjaga akun berapa banyak data yang dihitung sampai pengamatan tertentu.

F_yo Itu juga dikenal sebagai Frekuensi akumulasi absolut. Jika Anda membagi antara total data, Anda memiliki Frekuensi akumulasi relatif, yang jumlah terakhirnya harus sama dengan 1.

[TOC]

Rumus

Frekuensi akumulasi dari nilai variabel x tertentu_yo  Ini adalah jumlah frekuensi absolut f dari semua nilai lebih rendah dari atau sama dengan itu:

F_yo  = f₁ + F₂ + F₃  +… F_yo

Dengan menambahkan semua frekuensi absolut, jumlah total data n diperoleh, yaitu:

F₁ + F₂ + F₃ +.. . + F_N = N

Operasi sebelumnya ditulis dengan cara ringkasan dengan simbol jumlah ∑:

∑ f_yo = N

Frekuensi akumulasi lainnya

Frekuensi berikut juga dapat diakumulasikan:

-Frekuensi relatif: Itu diperoleh dengan membagi frekuensi absolut f_yo Antara total data n:

F_R = f_yo / N

Jika frekuensi relatif ditambahkan dari anak ke yang sesuai dengan pengamatan tertentu, Akumulasi frekuensi relatif. Nilai terakhir harus sama dengan 1.

-Akumulasi akumulasi persentase frekuensi: Frekuensi relatif akumulasi per 100% dikalikan.

F_% = (f_yo / N) x 100%

Frekuensi ini berguna untuk menggambarkan perilaku data, misalnya dengan menemukan langkah -langkah kecenderungan pusat.

Bagaimana mendapatkan frekuensi akumulasi?

Untuk mendapatkan frekuensi akumulasi, perlu memesan data dan mengaturnya dalam tabel frekuensi. Prosedur ini diilustrasikan dalam situasi praktis berikut:

Dapat melayani Anda: suksesi majemuk

-Di toko online yang menjual ponsel, catatan penjualan merek tertentu bulan Maret, nilai -nilai berikut per hari:

1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3

Variabelnya adalah Jumlah ponsel yang dijual sehari Dan itu kuantitatif. Data yang disajikan tidak begitu mudah untuk ditafsirkan, misalnya pemilik toko dapat tertarik mengetahui apakah ada tren, seperti hari -hari dalam seminggu ketika penjualan merek itu lebih besar.

Informasi seperti ini dan lebih banyak lagi, dapat diperoleh dengan menyajikan data secara tertib dan menentukan frekuensi.

Cara mengisi tabel frekuensi

Untuk menghitung frekuensi akumulasi, data dipesan:

 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5

Kemudian tabel dengan informasi berikut dibangun:

-Kolom pertama di sebelah kiri dengan jumlah ponsel yang dijual, antara 0 dan 5 dan dalam urutan yang meningkat.

-Kolom kedua: Frekuensi absolut, yang merupakan jumlah hari yang dijual 0 ponsel, 1 telepon, 2 telepon dan sebagainya.

-Kolom ketiga: frekuensi akumulasi, yang terdiri dari jumlah frekuensi sebelumnya ditambah frekuensi data yang akan dipertimbangkan.

Kolom ini dimulai dengan kolom pertama kolom frekuensi absolut, dalam hal ini adalah 0. Untuk nilai berikutnya, ini ditambahkan dengan yang sebelumnya. Dengan demikian, data terakhir dari frekuensi akumulasi dilanjutkan, yang harus bertepatan dengan total data.

Tabel Frecuency

Tabel berikut menunjukkan variabel "jumlah telepon yang dijual dalam satu hari", frekuensi absolutnya dan perhitungan terperinci dari akumulasi frekuensi.

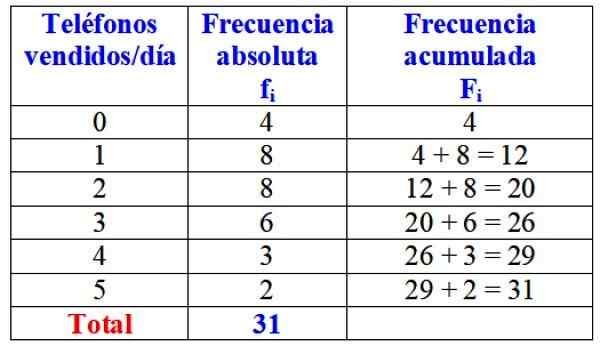Tabel frekuensi absolut dan akumulasi untuk variabel "telepon yang dijual per hari". Sumber: f. Zapata.

Dalam pandangan pertama, dapat dikatakan bahwa merek tersebut hampir selalu dijual satu atau dua ponsel per hari, karena frekuensi paling absolut adalah 8 hari, yang sesuai dengan nilai -nilai variabel ini. Hanya selama 4 hari dalam sebulan yang tidak menjual satu telepon pun.

Itu dapat melayani Anda: Alasan Trigonometri: Contoh, Latihan dan Aplikasi

Seperti dicatat, lebih mudah untuk memeriksa tabel daripada data longgar yang awalnya dikumpulkan.

Akumulasi distribusi frekuensi

Distribusi frekuensi akumulasi adalah tabel di mana frekuensi absolut, frekuensi akumulasi, akumulasi frekuensi relatif dan akumulasi frekuensi persentase tersedia.

Sementara keuntungan mengatur data dalam tabel seperti yang sebelumnya diperhatikan, jika nomor data sangat besar, ada kemungkinan bahwa tidak cukup untuk mengaturnya seperti yang ditunjukkan di atas, karena jika banyak frekuensi muncul, masih sulit untuk menafsirkan.

Masalahnya bisa jadi perbaikan dengan membangun a Distribusi frekuensi Dengan interval, prosedur yang berguna ketika variabel mengambil sejumlah besar nilai atau jika itu adalah variabel kontinu.

Di sini nilainya dikelompokkan ke dalam interval amplitudo yang sama, disebut kelas. Kelas ditandai dengan memiliki:

-Batas kelas: adalah nilai ekstrem dari setiap interval, ada dua, batas atas dan batas bawah. Secara umum, batas atas bukan milik interval tetapi dengan pengikut segera, sedangkan batas bawah tidak ada.

-Merek kelas: Itu adalah titik tengah dari setiap interval, dan dianggap sebagai nilai representatifnya.

-Lebar kelas: Ini dihitung dengan mengurangi nilai jurusan dan terkecil (kisaran) dan membaginya dengan jumlah kelas:

Lebar kelas = rentang / jumlah kelas

Maka elaborasi distribusi frekuensi terperinci.

Contoh

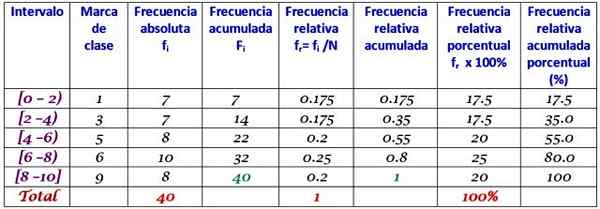
Kumpulan data ini sesuai dengan 40 nilai ujian matematika, pada skala dari 0 hingga 10:

0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.

Distribusi frekuensi dengan sejumlah kelas dapat dikembangkan, misalnya 5 kelas. Harus diingat bahwa ketika menggunakan banyak kelas, data tidak mudah untuk ditafsirkan dan rasa melaksanakan kelompok hilang.

Dapat melayani Anda: berapa banyak yang harus Anda tambahkan ke 3/4 untuk mendapatkan 6/7?

Dan jika sebaliknya mereka dikelompokkan dalam sedikit, maka informasinya diencerkan dan bagian darinya hilang. Itu semua tergantung pada jumlah data yang Anda miliki.

Dalam contoh ini adalah ide yang baik untuk memiliki dua skor di setiap interval, karena ada 10 skor dan 5 kelas akan dibuat. Peringkatnya adalah pengurangan antara peringkat utama dan terkecil, lebar kelas adalah:

Lebar kelas = (10-0)/5 = 2

Interval ditutup oleh kiri dan terbuka di sebelah kanan (kecuali yang terakhir), yang dilambangkan dengan kurung persegi dan tanda kurung masing -masing. Semua memiliki lebar yang sama, tetapi tidak wajib meskipun paling sering.

Setiap interval berisi sejumlah elemen atau frekuensi absolut, dan di kolom berikut adalah frekuensi akumulasi, di mana jumlah tersebut dibawa. Tabel juga menunjukkan frekuensi relatif f_R  (frekuensi absolut antara jumlah total data) dan persentase persentase persentase f_R × 100%.

Latihan yang diusulkan

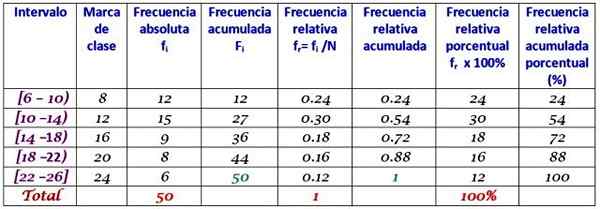
Perusahaan melakukan panggilan harian kepada pelanggannya selama dua bulan pertama tahun ini. Data adalah sebagai berikut:

6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 13, 17, 14, 26, 7, 12, 24, 7, 7

Grup dalam 5 kelas dan membangun tabel dengan distribusi frekuensi.

Menjawab

Lebar kelasnya adalah:

(26-6)/5 = 4

Cobalah untuk menyelesaikannya sebelum melihat jawabannya.

Referensi

1. Berenson, m. 1985. Statistik untuk Administrasi dan Ekonomi. Inter -American s.KE.
2. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
3. Levin, r. 1988. Statistik untuk administrator. 2nd. Edisi. Prentice Hall.
4. Probabilitas dan statistik. Lebar interval kelas. Diperoleh dari: pedroprobababilitas dan stadiistik.Blogspot.com.
5. Spiegel, m. 2009. Statistik. Seri Schaum. 4 ta. Edisi. Bukit McGraw.
6. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.