Formula frekuensi absolut, perhitungan, distribusi, contoh

Itu Frecuency absolut Itu didefinisikan sebagai berapa kali data yang sama diulang dalam rangkaian pengamatan variabel numerik. Jumlah semua frekuensi absolut setara dengan total data.

Ketika ada banyak nilai variabel statistik, lebih mudah untuk mengaturnya dengan benar untuk mengekstrak informasi tentang perilaku mereka. Informasi tersebut diberikan oleh langkah -langkah kecenderungan pusat dan langkah -langkah dispersi.

Gambar 1. Frekuensi absolut dari pengamatan statistik adalah kunci untuk menemukan tren yang mengikuti kumpulan data

Dalam perhitungan langkah -langkah ini, data diwakili melalui frekuensi yang muncul dalam semua pengamatan.

Contoh berikut menunjukkan bagaimana mengungkapkan frekuensi absolut dari setiap data. Selama paruh pertama Mei, ini adalah ukuran kostum koktail terbaik, dari gudang pakaian wanita yang terkenal:

8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18

Berapa banyak gaun yang dijual dalam ukuran tertentu, misalnya ukuran 10? Pemilik tertarik untuk mengetahui pesanan.

Memesan data lebih mudah dihitung, ada total 30 pengamatan, daripada yang dipesan dari yang terkecil ke yang tertinggi seperti ini:

4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18

Dan sekarang terbukti bahwa ukuran 10 diulang 6 kali, oleh karena itu frekuensi absolutnya sama dengan 6. Prosedur yang sama dilakukan untuk mengetahui frekuensi absolut dari ukuran yang tersisa.

[TOC]

Rumus

Frekuensi absolut, dilambangkan sebagai f_yo, Itu sama dengan jumlah kali sebagai nilai x tertentu_yo berada dalam kelompok pengamatan.

Dengan asumsi bahwa total pengamatan adalah dari nilai n, jumlah dari semua frekuensi absolut harus sama dengan angka tersebut:

Dapat melayani Anda: papomudas

∑f_yo = f₁ + F₂ + F₃ +… F_N = N

Frekuensi lain

Jika setiap nilai f_yo Itu dibagi dengan jumlah total data n, Anda memiliki Frekuensi relatif F_R nilai x_yo:

F_R = f_yo / N

Frekuensi relatif adalah nilai antara 0 dan 1, karena n selalu lebih besar dari f_yo, Tetapi jumlahnya harus sama dengan 1.

Mengalikan 100 hingga setiap nilai f_R kamu punya Frekuensi persentase relatif, yang jumlahnya 100%:

Frekuensi persentase relatif = (f_yo / N) x 100%

Itu juga penting frekuensi akumulasi F_yo Sampai pengamatan tertentu, ini adalah jumlah dari semua frekuensi absolut sampai pengamatan tersebut termasuk:

F_yo = f₁ + F₂ + F₃ +… F_yo

Jika frekuensi akumulasi dibagi dengan jumlah total data n, Anda memiliki Akumulasi frekuensi relatif, yang berlipat ganda per 100 menghasilkan akumulasi persentase frekuensi relatif.

Bagaimana mendapatkan frekuensi absolut?

Untuk menemukan frekuensi absolut dari nilai tertentu yang dimiliki oleh kumpulan data, semuanya diatur dari yang paling kecil ke yang terbesar dan nilainya dihitung.

Dalam contoh ukuran gaun, frekuensi absolut ukuran 4 adalah 3 gaun, yaitu f₁ = 3. Untuk ukuran 6, 4 gaun terjual: f₂ = 4. Dalam ukuran 8 4 gaun juga dijual, f₃ = 4 dan seterusnya.

Tabulasi

Hasil total dapat diwakili dalam tabel yang menunjukkan frekuensi absolut masing -masing:

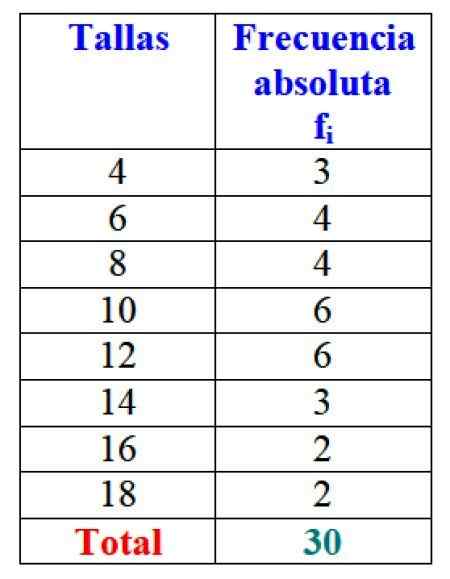Gambar 2. Tabel yang mewakili variabel "penjualan penjualan" dan frekuensi absolut masing -masing. Sumber: f. Zapata.

Jelas menguntungkan untuk memesan informasi dan dapat mengaksesnya, alih -alih bekerja dengan data longgar.

Penting: Perhatikan bahwa dengan menambahkan semua nilai kolom f_yo  Jumlah total data selalu diperoleh. Jika tidak, akuntansi harus ditinjau, karena ada kesalahan.

Tabel frekuensi yang diperluas

Tabel sebelumnya dapat diperpanjang dengan menambahkan jenis frekuensi lain di kolom berturut -turut di sebelah kanan:

Dapat melayani Anda: homokedastisitas: apa itu, penting dan contoh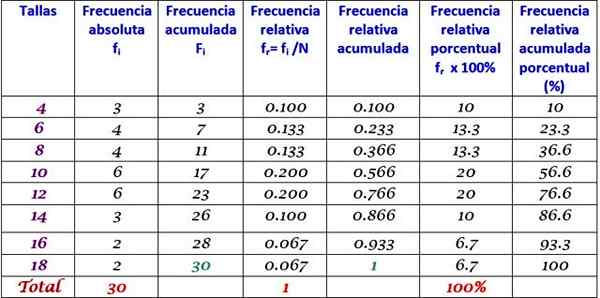

Distribusi frekuensi

Distribusi frekuensi adalah hasil pengorganisasian data dalam hal frekuensi mereka. Saat bekerja dengan banyak data, lebih mudah untuk mengelompokkannya ke dalam kategori, interval atau kelas, masing -masing dengan frekuensi masing -masing: absolut, relatif, akumulasi dan persentase.

Tujuan dari melakukannya adalah untuk lebih mudah mengakses informasi yang berisi data, serta menafsirkannya dengan benar, yang tidak dimungkinkan ketika mereka disajikan tanpa pesanan.

Dalam contoh ukuran, data tidak dikelompokkan, karena mereka tidak terlalu banyak ukuran dan dapat dengan mudah dimanipulasi dan dihitung. Variabel kualitatif juga dapat dikerjakan dengan cara ini, tetapi ketika data sangat banyak, mereka bekerja dengan lebih baik mengelompokkannya di kelas.

Distribusi frekuensi untuk data yang dikelompokkan

Untuk mengelompokkan data di kelas dengan ukuran yang sama, berikut ini harus dipertimbangkan:

-Ukuran, lebar atau amplitudo kelas: Itu adalah perbedaan antara nilai terbesar kelas dan anak di bawah umur.

Ukuran kelas diputuskan dengan membagi kisaran R dengan jumlah kelas yang perlu dipertimbangkan. Kisarannya adalah perbedaan antara nilai maksimum data dan minor, seperti ini:

Ukuran kelas = rentang / jumlah kelas.

-Batas kelas: interval yang naik dari batas bawah ke batas atas kelas.

-Merek kelas: Itu adalah titik tengah interval, yang dianggap mewakili kelas. Itu dihitung dengan semi -terbatas batas atas dan batas bawah kelas.

-Jumlah kelas: Formula Sturges dapat digunakan:

Kelas = 1 + 3.322 log n

Dimana n adalah jumlah kelas. Seperti biasanya angka desimal, berikut ini dibulatkan.

Contoh

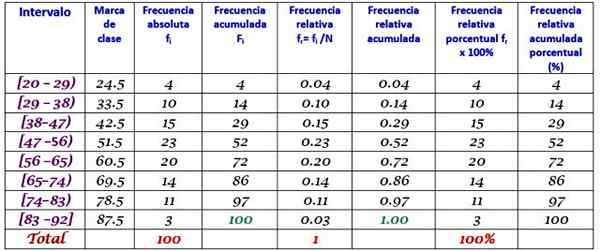
Mesin pabrik besar tidak beroperasi, karena mengalami kegagalan berulang. Periode tidak aktif berturut -turut dalam hitungan menit, mesin tersebut, dicatat di bawah ini, dengan total 100 data:

Itu dapat melayani Anda: probabilitas frekuensi: konsep, bagaimana itu dihitung dan contoh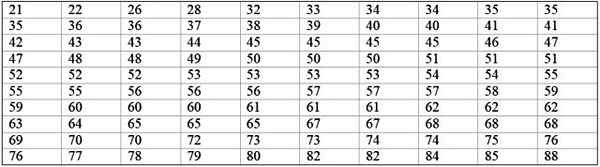

Pertama, jumlah kelas ditentukan:

Kelas = 1 + 3.322 log n = 1 + 3.32 log 100 = 7.64 ≈ 8

Ukuran kelas = rentang / jumlah kelas = (88-21) / 8 = 8.375

Ini juga merupakan angka desimal, jadi dibutuhkan 9 sebagai ukuran kelas.

Merek kelas adalah rata-rata antara batas atas dan bawah kelas, misalnya untuk kelas [20-29) ada tanda dari:

Class Brand = (29 + 20) / 2 = 24.5

Lanjutkan dengan cara yang sama untuk menemukan merek kelas dari interval yang tersisa.

Olahraga diselesaikan

40 orang muda mengindikasikan bahwa waktu dalam hitungan menit yang berlalu di internet Minggu lalu adalah yang berikutnya, diperintahkan semakin:

0; 12; dua puluh; 35; 35; 38; 40; Empat. Lima; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.

Itu diminta untuk membangun distribusi frekuensi data ini.

Larutan

Peringkat r dari set N = 40 data adalah:

R = 220 - 0 = 220

Penerapan formula Sturges untuk menentukan jumlah kelas menghasilkan hasil berikut:

Kelas = 1 + 3.322 log n = 1 + 3.32 log 40 = 6.3

Seperti desimal, keseluruhan langsung adalah 7, oleh karena itu data dikelompokkan menjadi 7 kelas. Setiap kelas memiliki lebar:

Ukuran kelas = rentang / jumlah kelas = 220/7 = 31.4

Nilai dekat dan bulat adalah 35, oleh karena itu lebar kelas 35 dipilih.

Tanda kelas dihitung rata -rata batas atas dan bawah setiap interval, misalnya, untuk interval [0,35):

Class Brand = (0+35)/2 = 17.5

Kami melanjutkan dengan cara yang sama dengan kelas yang tersisa.

Akhirnya, frekuensi dihitung sesuai dengan prosedur yang dijelaskan di atas, menghasilkan distribusi berikut:

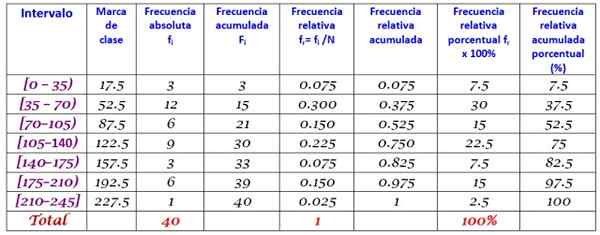
Referensi

1. Berenson, m. 1985. Statistik untuk Administrasi dan Ekonomi. Inter -American s.KE.
2. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
3. Levin, r. 1988. Statistik untuk administrator. 2nd. Edisi. Prentice Hall.
4. Spiegel, m. 2009. Statistik. Seri Schaum. 4 ta. Edisi. Bukit McGraw.
5. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.