Karakteristik fungsi yang terhuyung -huyung, contoh, latihan

Itu fungsi terhuyung -huyung y = s (x) adalah fungsi yang didefinisikan dalam potongan atau bagian, sehingga dalam interval terbatas [a, b] memiliki jumlah diskontinuitas yang terbatas, yang akan kita sebut x₀ < x₁ < x₂ <… . x_N.  Di setiap interval terbuka (x_yo , X_i+1), dan memiliki nilai konstan nilai s_yo, Dengan diskontinuitas -saltos- pada poin x_yo.

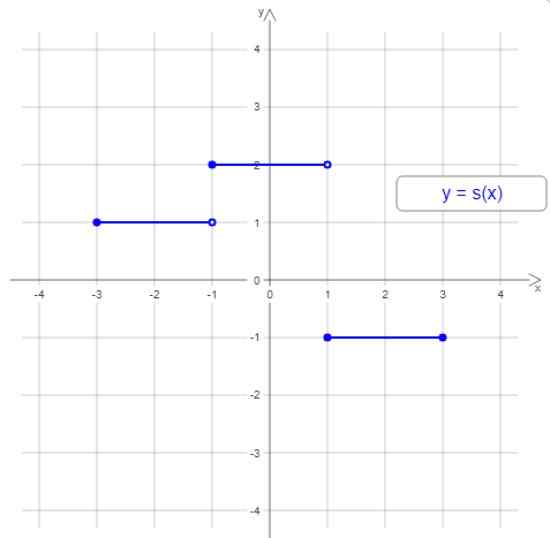
Grafik yang dihasilkan dari fungsi seperti ini terdiri dari langkah atau langkah. Mari kita lihat contoh di bawah ini:

Gambar 1. Contoh fungsi terhuyung -huyung. Sumber: Wikimedia Commons.

Grafik fungsi loncatan ini memiliki tiga langkah atau interval yang terhuyung -huyung, tetapi secara umum fungsi terhuyung -huyung dapat memiliki jumlah langkah berapa pun. Lebar langkah -langkahnya bisa berbeda dan tangga tidak selalu naik atau turun.

Fungsi terhuyung -huyung dari contoh dapat ditulis menentukan lebar dan tinggi dari setiap langkah, seperti ini:

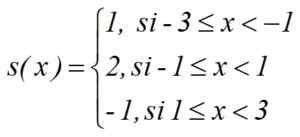
[TOC]

Karakteristik fungsi melangkah

-Fungsi menerima namanya dengan grafik dalam bentuk langkah, yang diberikan oleh segmen yang menyusunnya. Setiap segmen memiliki bagian dari domain fungsi dan di masing -masing, fungsinya konstan.

-Domain fungsi yang terhuyung -huyung adalah nilai -nilai yang dimiliki oleh interval yang didefinisikannya: [a, b], sedangkan rentang dibentuk oleh nilai -nilai s_yo ketinggian langkah.

Dalam contoh Gambar 1, domain adalah interval [-3,3] dan kisarannya adalah nilai -1, 1 dan 2.

-Fungsi terhuyung -huyung kontinu kecuali dalam nilai yang membatasi setiap langkah, poin x_yo.

-Fungsi Escalonada dapat ditambahkan dan dikalikan untuk memunculkan fungsi loncatan baru.

-Turunannya adalah 0 untuk titik -titik di mana ia didefinisikan, karena di dalamnya fungsinya konstan. Untuk bagiannya, turunannya tidak ada dalam diskontinuitas.

-Integral dari fungsi loncatan s (x) antara ke Dan B Itu ada dan sesuai dengan jumlah area persegi panjang lebar x_yo- X_I-1 dan tinggi s_k, sama dengan langkah.

Dapat melayani Anda: Acara Independen: Demonstrasi, Contoh, Latihan

Karena area persegi panjang adalah produk dari pangkalan dengan tinggi, kita harus:

Contoh fungsi terhuyung -huyung

Di dalam fungsi terhuyung -huyung ada beberapa jenis, misalnya fungsi seluruh bagian dan fungsinya Langkah kesatuan, serta berbagai fungsi terhuyung -huyung yang menggambarkan situasi umum, seperti tingkat banyak layanan. Mari kita lihat beberapa contoh:

- Contoh 1: Seluruh Pihak

Seluruh fungsi bagian sering menggunakan braket ganda:

f (x) = [[x]]

Dan didefinisikan sebagai fungsi yang menetapkan ke setiap bilangan real bilangan bulat terdekat atau lebih kecil, mengabaikan desimal yang memiliki angka. Seperti kasusnya, kami memiliki:

Fungsi Atap atau Langit

Memberikan nilai domain kepada setiap bilangan bulat terdekat secara berlebihan. Misalnya:

[+2.56]] = 3

Bagian desimal yang 0 diabaikan.56 dan bilangan bulat terdekat ditugaskan yang lebih besar dari 2.

Contoh lain:

[-4.2]]= -3

Sekali lagi bagian desimal 0 dihilangkan.2 dan bilangan bulat terbesar tertinggi lebih dekat ke -4 diambil sebagai nilai fungsi, yaitu -3.

Pada gambar berikut adalah grafik fungsi langit -langit, perhatikan bahwa langkah dibatasi oleh lingkaran berlubang kecil ke kiri dan satu penuh ke kanan, karena sejumlah interval, bilangan bulat terbesar ditetapkan di antara ujung -ujungnya di antara ujungnya berakhir di antara ujung interval.

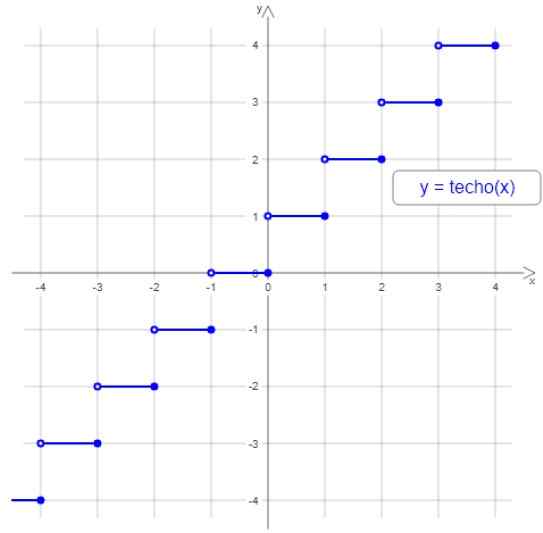Gambar 2. Atap atau fungsi langit. Sumber: Wikimedia Commons.

Misalnya, semua nilai antara 3 dan 4 ditetapkan seluruh 4, yaitu -2 dan -1 ditugaskan -1 dan seterusnya.

Fungsi lantai atau tanah

Menetapkan nilai domain masing -masing angka keseluruhan terdekat secara default. Contoh fungsi ini adalah:

Dapat melayani Anda: berapa persepuluh yang ada di satu unit?

[[+3.7]] = 3

[[-1.5]] = -2

[[π]] = 3

Kedua fungsi itu kontinu kecuali untuk bilangan bulat, di mana lompatan disajikan, dan konstan untuk nilai -nilai antara bilangan bulat k dan k+1.

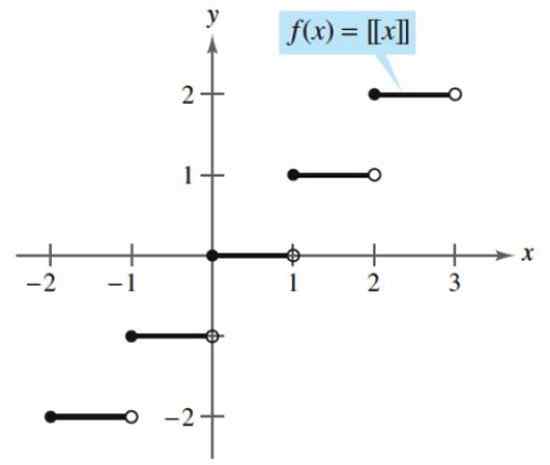Gambar 3. Fungsi lantai atau tanah. Sumber: Larson, R. Perhitungan variabel.

- Contoh 2

Di kota, tarif taksi adalah 3.$ 65, untuk 100 m pertama. Dan untuk setiap 100 m adalah 0.$ 18, menjadi batas per rute 50 km.

Diinginkan untuk menetapkan fungsi yang menghubungkan rute dalam meter dengan biaya layanan dengan $, yang harus memiliki formulir ini:

f (x) = 3.65 + 0.18. [[x /100]] $

Di mana seluruh fungsi bagian dapat dari fungsi langit, di mana laju dasar yang ditambahkan 3.$ 65. Misalnya, jika kita ingin tahu berapa banyak yang akan dibayar untuk perjalanan 6.25 km = 6250 m, kami akan memiliki:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 15.$ 65

Jika perusahaan taksi memilih fungsi lantai, maka klien akan membayar sedikit lebih sedikit untuk perjalanan:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 14.$ 65

Latihan terpecahkan

- Latihan 1

Panggilan Jarak Jauh Antara Kota A dan B Biaya 0.40 $ 10 menit. Setelah periode itu, fraksi atau menit tambahan bernilai 0.05 $.

Ekspresikan biaya c (t) dari panggilan yang berlangsung selama beberapa menit.

Larutan

Kami dapat mengekspresikan fungsi ini jika kami menganalisis apa yang terjadi dengan setiap opsi selama durasi panggilan:

Untuk t ≤ 10 menit

Ketika t, yang merupakan waktu panggilan berlangsung, kurang dari atau sama dengan 10 menit, dibayar 0.$ 40.

Dapat melayani Anda: 2 -digit divisi diselesaikan

Karena itu:

f (t) = 0.$ 40 untuk T termasuk antara 0 dan 10 menit.

Kami sudah memiliki bagian dari fungsi.

Untuk t> 10 menit

Kasus Entero t

Sekarang mari kita lihat apa yang terjadi ketika waktu t = 10 menit terlampaui: mungkin terjadi kelebihannya adalah bilangan bulat, misalnya percakapan berlangsung tepatnya 11, 12, 13, 14 menit atau lebih. Dalam hal ini jumlah panggilannya adalah:

f (t) = 0.40 + 0.05 (T-10) $, untuk T lebih dari 10 menit, dengan seluruh t.

Artinya dalam hal ini: t = 11, 12, 13, 14, 15 ... menit.

Misalnya, misalkan percakapan berlangsung tepat 15 menit, biayanya adalah:

f (15) = 0.40 + 0.05 (15-10) $ = 0.$ 65

Kasus desimal

Akhirnya, pertimbangkan kasus di mana panggilan berlangsung untuk sementara waktu dengan bagian desimal. Misalnya, misalkan panggilan itu berlangsung 15 menit dan 45 detik, yang akan menjadi desimal 15.75 menit.

Kami dapat mengekspresikannya dalam hal seluruh bagian dari jenis lantai, dengan asumsi bahwa perusahaan ingin memberikan lebih banyak manfaat kepada klien, atau langit:

f (t) = 0.40 + 0.05 ⋅ [[T-9]] $

Mari kita lihat apa yang akan dibayar klien jika itu adalah fungsi lantai:

F (15.75) = 0.40 + 0.05 ⋅ [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 6 $ = 0.$ 70.

Atau sebagai fungsi langit, dalam hal ini biayanya adalah:

F (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 7 $ = 0.75 $.

Fungsi dan grafik

Sebagai fungsi yang ditentukan oleh bagian -bagiannya adalah:

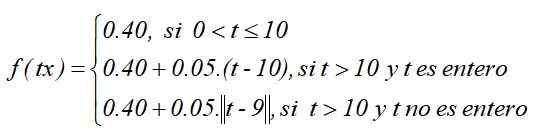
Grafik fungsi akan seperti ini, dengan asumsi bahwa seluruh fungsi jenis langit -langit dipilih:

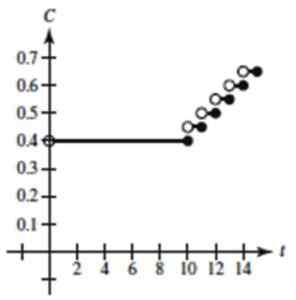Gambar 4. Grafik fungsi melangkah dari latihan diselesaikan 1. Sumber: Larson, R. Perhitungan variabel.

- Latihan 2

Hitung ∫s integral (x) DX antara -3 dan 3 dari fungsi loncatan:

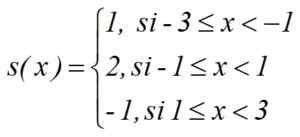
Larutan

Kami menerapkan definisi untuk integral fungsi yang terhuyung -huyung:

Oleh karena itu integral yang dicari I adalah:

I = 1. [(-1)-(-3)] + 2.[1- (-1)]+(-1).[3-1] = 2+4-2 = 4

Referensi

1. Jiménez, r. 2006.Fungsi Matematika. Pendidikan Pearson.
2. Larson, r. 2010. Perhitungan variabel. 9NA. Edisi. Bukit McGraw.
3. Matematika iv. Fungsi. Pulih dari: Cobaqroo.Edu.MX.
4. Wikipedia. Seluruh bagian fungsi. Pulih dari: is.Wikipedia.org.
5. Wikipedia. Fungsi terhuyung -huyung. Pulih dari: is.Wikipedia.org.