Fungsi suntikan apa yang terdiri darinya, untuk apa dan contohnya

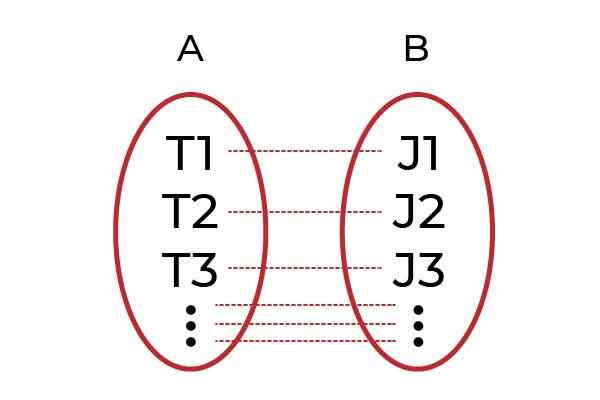
A Fungsi suntikan Ini adalah hubungan elemen domain dengan satu elemen kodominium tunggal. Juga dikenal sebagai fungsi satu per satu ( sebelas ), adalah bagian dari klasifikasi fungsi mengenai cara di mana elemen mereka terkait.

Elemen kodominium hanya dapat menjadi gambar elemen tunggal dari domain, dengan cara ini nilai -nilai variabel dependen tidak dapat diulangi.

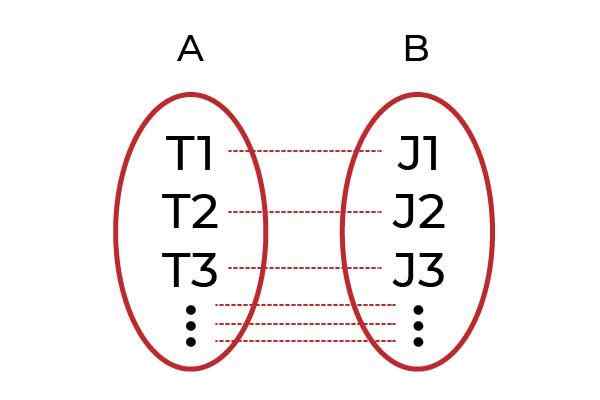
Sumber: Penulis.

Contoh yang jelas adalah untuk mengelompokkan pria dengan pekerjaan di grup A, dan di grup B untuk semua bos. Fungsinya F Itu akan menjadi orang yang mengaitkan setiap pekerja dengan bos mereka. Jika setiap pekerja dikaitkan dengan bos yang berbeda F, Jadi F  Itu akan menjadi satu Fungsi suntikan.

Mempertimbangkan Suntikan Berikut ini harus dipenuhi ke suatu fungsi:

∀ x₁  ≠ x₂   ⇒ f (x₁ ) ≠ f (x₂ )

Ini adalah cara aljabar untuk mengatakan Untuk semua x₁ berbeda dari x₂ Anda memiliki f (x₁ ) Berbeda dari f (x₂ ).

[TOC]

Untuk apa fungsi suntikan?

Suntikan adalah properti fungsi kontinu, karena mereka memastikan alokasi gambar untuk setiap elemen domain, aspek penting dalam kesinambungan suatu fungsi.

Saat menggambar garis sejajar dengan sumbu X Pada grafik fungsi injeksi, hanya grafik yang harus disentuh pada satu titik, terlepas dari berapa tinggi atau besarnya DAN Garis ditarik. Ini adalah cara grafis untuk membuktikan injektifitas suatu fungsi.

Cara lain untuk menguji jika suatu fungsi Suntikan, sedang membersihkan variabel independen X Dalam hal variabel dependen DAN. Maka harus diverifikasi jika domain ekspresi baru ini berisi bilangan real, pada saat yang sama seperti untuk setiap nilai dari DAN ada satu nilai X.

Fungsi pesanan atau hubungan mematuhi, di antara bentuk -bentuk lain, notasi F: d_F→C_F

Itu berbunyi F yang berubah dari D_F ke c_F

Dimana fungsinya F Hubungkan set Domain Dan Kodominium. Juga dikenal sebagai set awal dan set kedatangan.

Dapat melayani Anda: pengambilan sampel acak: metodologi, kelebihan, kerugian, contoh

Dominion D_F  Berisi nilai yang diizinkan untuk variabel independen. Kodominium C_F  Itu dibentuk oleh semua nilai yang tersedia untuk variabel dependen. Elemen C_F berhubungan dengan D_F  Mereka tahu caranya Rentang fungsi (r_F ).

Pengkondisian fungsi

Terkadang fungsi yang tidak suntikan, dapat menjalani pengkondisian tertentu. Kondisi baru ini dapat mengubahnya menjadi a Fungsi suntikan. Semua jenis modifikasi pada domain dan kodominium fungsi valid, di mana tujuannya adalah untuk memenuhi sifat injektifitas dalam hubungan yang sesuai.

Contoh fungsi suntikan dengan latihan terpecahkan

Contoh 1

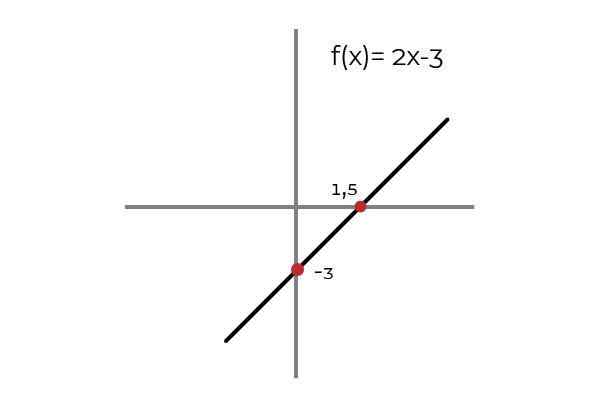
Jadilah fungsinya F: r → R ditentukan oleh garis F (x) = 2x - 3

A: [semua bilangan real]

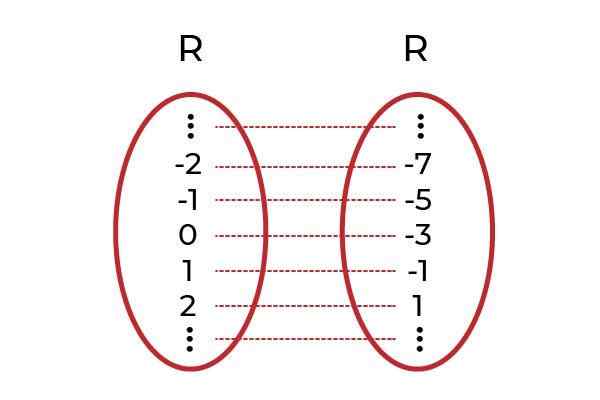
Sumber: Penulis.

Diamati bahwa untuk nilai domain apa pun ada gambar dalam kodominium. Gambar ini unik, yang menjadikan F fungsi injeksi. Ini berlaku untuk semua fungsi linier (fungsi yang tingkat variabelnya lebih besar adalah satu).

Sumber: Penulis.

Contoh 2

Jadilah fungsinya F: r → R didefinisikan oleh F (x) = x² +1

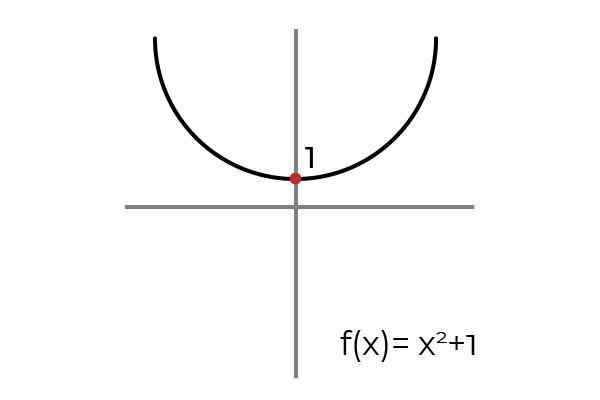Sumber: Penulis

Saat menggambar garis horizontal, diamati bahwa grafik ditemukan pada lebih dari satu kesempatan. Karena ini fungsinya F tidak suntikan saat didefinisikan  R → R

Domain fungsi dikondisikan:

                                               F: r⁺ ATAU 0 → R

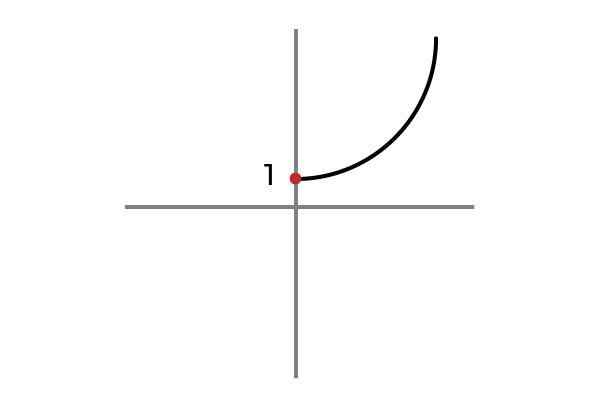Sumber: Penulis

Sekarang variabel independen tidak mengambil nilai negatif, dengan cara ini dihindari untuk mengulang hasil dan fungsinya F: r⁺ ATAU 0 → R didefinisikan oleh F (x) = x² + 1 adalah suntikan.

Solusi homolog lainnya adalah membatasi domain ke kiri, yaitu, membatasi fungsi hanya mengambil nilai negatif dan nol.

Domain fungsi dikondisikan

                                               F: r^- ATAU 0 → R

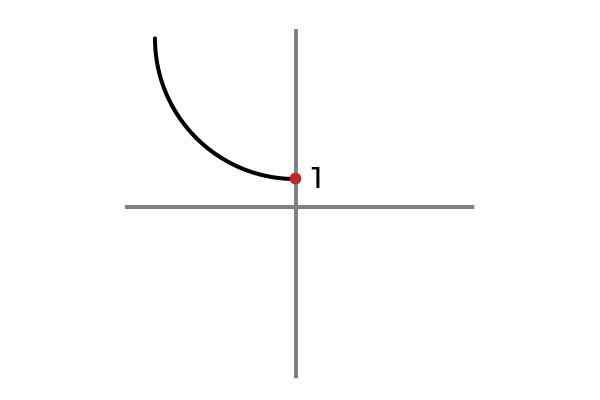Sumber: Penulis

Sekarang variabel independen tidak mengambil nilai negatif, dengan cara ini dihindari untuk mengulang hasil dan fungsinya F: r^- ATAU 0 → R didefinisikan oleh F (x) = x² + 1 adalah suntikan.

Fungsi trigonometri memiliki perilaku yang mirip dengan gelombang, di mana sangat umum untuk menemukan pengulangan nilai dalam variabel dependen. Melalui pengkondisian spesifik, berdasarkan pengetahuan sebelumnya tentang fungsi -fungsi ini, kami dapat membatasi domain untuk memenuhi kondisi injektif.

Dapat melayani Anda: Coplanares Points: Persamaan, Contoh, dan Latihan Terpecahkan

Contoh 3

Jadilah fungsinya F: [ -π/2, π/2 ] → R didefinisikan oleh F (x) = cos (x)

Dalam interval [ -π/2 → π/2 ] Fungsi kosinus memvariasikan hasilnya antara nol dan satu.

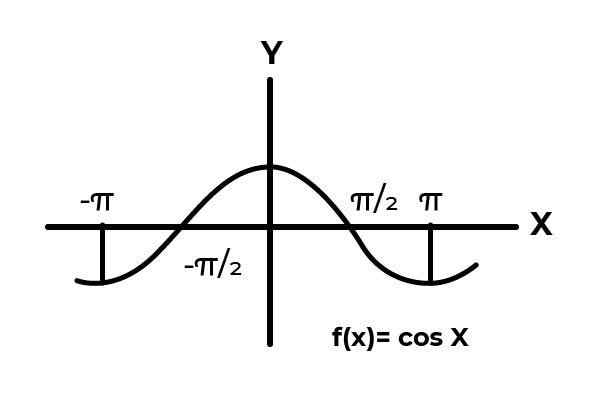Sumber: Penulis.

Seperti yang dapat dilihat dalam grafik. Mulailah dari awal x = -π/2 kemudian mencapai maksimum nol. Itu setelah x = 0 bahwa nilainya mulai mengulang, sampai kembali ke nol masuk x = π/2. Dengan cara ini diketahui itu F (x) = cos (x) tidak suntikan Untuk interval [ -π/2, π/2 ] .

Saat mempelajari grafik fungsi F (x) = cos (x) Interval diamati di mana perilaku kurva beradaptasi dengan kriteria injektivitas. Seperti interval

[0 , π ]

Di mana fungsi bervariasi dari 1 hingga -1, tanpa mengulangi nilai apa pun dalam variabel dependen.

Dengan cara ini fungsi fungsi F: [0 , π ] → R didefinisikan oleh F (x) = cos (x). Itu suntikan

Ada fungsi non -linier di mana kasus serupa disajikan. Untuk ekspresi rasional, di mana denominator menampung setidaknya satu variabel, ada batasan yang mencegah injektifitas hubungan.

Contoh 4

Jadilah fungsinya F: r → R didefinisikan oleh F (x) = 10/x

Fungsi didefinisikan untuk semua bilangan real kecuali 0 yang menyajikan ketidakpastian (tidak dapat dibagi antara nol).

Saat mendekati nol di sebelah kiri variabel dependen membutuhkan nilai negatif yang sangat besar, dan segera setelah nol, nilai variabel dependen mengambil angka positif yang besar.

Gangguan ini membuat ekspresi F: r → R didefinisikan oleh F (x) = 10/x

Jangan suntikan.

Seperti yang terlihat pada contoh sebelumnya, pengecualian nilai -nilai dalam domain berfungsi untuk "memperbaiki" ketidakpastian ini. Zero dikecualikan dari domain, meninggalkan set dan set kedatangan yang didefinisikan sebagai berikut:

R - 0 → R

Di mana R - 0 melambangkan yang nyata kecuali untuk satu set yang satu -satunya elemen adalah nol.

Dengan cara ini ekspresi F: r - 0 → R didefinisikan oleh F (x) = 10/x adalah suntikan.

 Contoh 5

Jadilah fungsinya F: [0 , π ] → R didefinisikan oleh F (x) = sin (x)

Dalam interval [0 , π ] Fungsi sinus memvariasikan hasilnya antara nol dan satu.

Dapat melayani Anda: variabel acak: konsep, jenis, contoh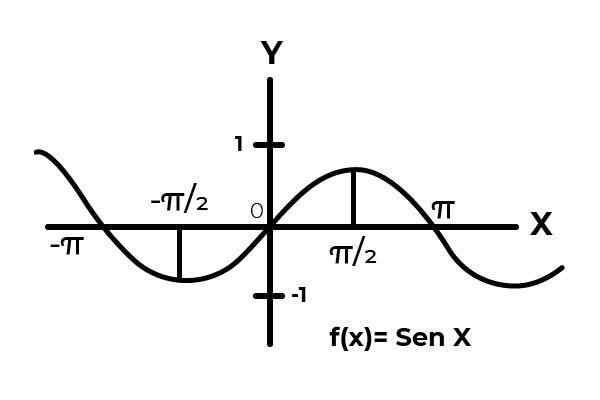Sumber: Penulis.

Seperti yang dapat dilihat dalam grafik. Mulailah dari awal x = 0 kemudian mencapai maksimal x = π/2. Itu setelah x = π/2 bahwa nilai mulai diulang, sampai kembali ke nol masuk x = π. Dengan cara ini diketahui itu F (x) = sin (x) tidak suntikan Untuk interval [0 , π ] .

Saat mempelajari grafik fungsi F (x) = sin (x) Interval diamati di mana perilaku kurva beradaptasi dengan kriteria injektivitas. Seperti interval  [  π/2,3π/2  ]

Di mana fungsi bervariasi dari 1 hingga -1, tanpa mengulangi nilai apa pun dalam variabel dependen.

Dengan cara ini fungsinya F: [  π/2,3π/2  ] → R didefinisikan oleh F (x) = sin (x). Itu suntikan

Contoh 6

Verifikasi jika fungsinya F: [0, ∞) → R didefinisikan oleh F (x) = 3x² Itu suntikan.

Pada kesempatan ini domain ekspresi sudah terbatas. Juga diamati bahwa nilai variabel dependen tidak diulang dalam interval ini.

Oleh karena itu dapat disimpulkan itu F: [0, ∞) → R didefinisikan oleh F (x) = 3x²   Itu suntikan

Contoh 7

Identifikasi fungsinya yang mana

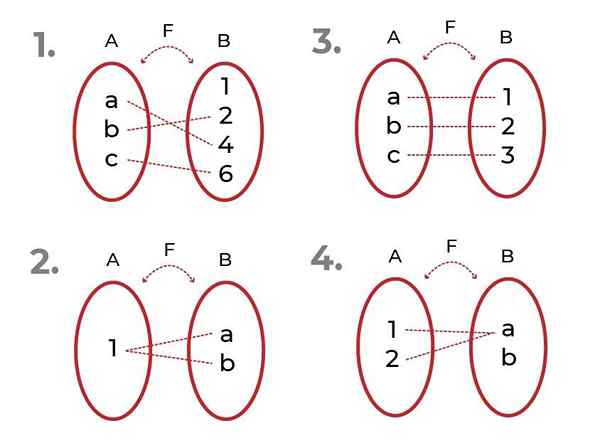Sumber: Penulis

1. Itu suntikan. Elemen terkait kodominium unik untuk setiap nilai variabel independen.
2. Itu tidak suntikan. Ada elemen co -oominium yang terkait dengan lebih dari satu elemen set awal.
3. Itu suntikan
4. Itu tidak suntikan

Latihan yang diusulkan untuk kelas/rumah

Verifikasi jika fungsi berikut adalah injeksi:

F: [0, ∞) → R didefinisikan oleh F (x) = (x + 3)²  

F: [ π/2,3π/2  ] → R didefinisikan oleh F (x) = tan (x)

F: [ -π,π  ] → R didefinisikan oleh F (x) = cos (x + 1)

F: r → R ditentukan oleh garis F (x) = 7x + 2

Referensi

1. Pengantar logika dan pemikiran kritis. Merrilee h. Ikan salmon. Universitas Pittsburgh
2. Masalah dalam analisis matematika. Piotr Bilar, Alfred Witkowski. Universitas Wroclaw. Tiang.
3. Elemen analisis abstrak. Mícheál O'Searcoid PhD. Departemen Matematika. University College Dublin, Beldfield, Dublind 4.
4. Pengantar logika dan metodologi ilmu deduktif. Alfred Tarski, New York Oxford. Oxford University Press.
5. Prinsip Analisis Matematika. Enrique Linés Escardó. Editorial Reverté s. Hingga 1991. Barcelona, ​​Spanyol.