Fungsi berlebihan, sifat, contoh

A fungsi berlebihan Ini adalah hubungan apa pun di mana setiap elemen milik kodominium adalah gambar dari setidaknya satu elemen domain. Juga dikenal sebagai fungsi tentang, Mereka adalah bagian dari klasifikasi fungsi mengenai cara elemen mereka terkait.

Misalnya suatu fungsi F: a → B didefinisikan oleh F (x) = 2x

Yang dibaca "F itu berubah dari KE sampai B didefinisikan oleh F (x) = 2x "

Sentuh Tentukan set awal dan kedatangan A dan B.

A: 1, 2, 3, 4, 5 Sekarang nilai atau gambar yang masing -masing elemen ini akan dirilis saat dievaluasi F, Mereka akan menjadi elemen kodominium.

F (1) = 2

F (2) = 4

F (3) = 6

F (4) = 8

F (5) = 10

Sehingga membentuk set B: 2, 4, 6, 8, 10

Dapat disimpulkan bahwa itu:

F: 1, 2, 3, 4, 5  → 2, 4, 6, 8, 10 didefinisikan oleh F (x) = 2x adalah fungsi overjective

Setiap elemen kodominium harus setidaknya satu operasi variabel independen melalui fungsi yang dimaksud. Tidak ada pembatas gambar, elemen kodominium dapat menjadi gambar lebih dari satu elemen domain dan terus berurusan dengan a fungsi berlebihan.

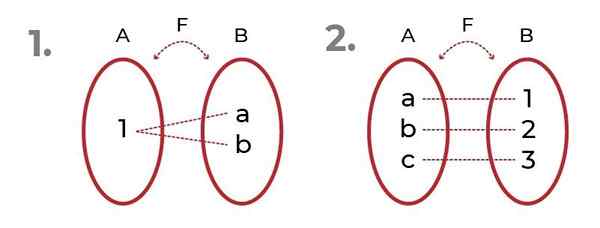
Gambar menunjukkan 2 contoh dengan Fungsi Onjective.

Sumber: Penulis

Pada yang pertama, diamati bahwa gambar dapat dirujuk ke elemen yang sama, tanpa mengorbankan Overjektivitas dari fungsi tersebut.

Di detik kita melihat distribusi yang adil antara domain dan gambar. Ini memunculkan Fungsi BYJECTIVE, dimana kriteria Fungsi suntikan dan fungsi berlebihan.

Metode lain untuk mengidentifikasi Fungsi Onjective, adalah untuk memverifikasi apakah kodominium sama dengan peringkat fungsi. Ini berarti bahwa jika set kedatangan sama dengan gambar yang disediakan oleh fungsi saat mengevaluasi variabel independen, Fungsinya berlebihan.

[TOC]

Properti

Mempertimbangkan Overjective Berikut ini harus dipenuhi ke suatu fungsi:

Menjadi F: d_F → C_F

∀ B ℮ C_F  DAN untuk ℮  D_F   / F (a) = b

Ini adalah cara aljabar untuk menetapkan itu Untuk semua "b" milik c_F Ada "A" milik D_F  sedemikian rupa, fungsi F dievaluasi dalam "A" sama dengan "B". 

Itu dapat melayani Anda: sifat radikal

Overturtivitas adalah kekhasan fungsi, di mana kodominium dan peringkat serupa. Dengan demikian, elemen yang dievaluasi dalam fungsi membentuk set kedatangan.

Pengkondisian fungsi

Terkadang fungsi yang tidak Overjective, dapat menjalani pengkondisian tertentu. Kondisi baru ini dapat mengubahnya menjadi a fungsi berlebihan.

Semua jenis modifikasi pada domain dan kodominasi fungsi valid, di mana tujuannya adalah untuk memenuhi sifat overjectivity dalam hubungan yang sesuai.

Contoh: latihan terpecahkan

Untuk memenuhi persyaratan Overjektivitas Teknik pengkondisian yang berbeda harus diterapkan, ini untuk memastikan bahwa setiap elemen kodominium berada dalam set gambar fungsi.

Latihan 1

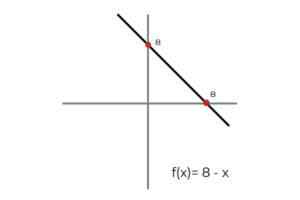
• Jadilah fungsinya F: r → R ditentukan oleh garis F (x) = 8 - x

A: [semua bilangan real]

Sumber: Penulis

Dalam hal ini, fungsi tersebut menggambarkan garis kontinu, yang mencakup semua bilangan real baik di domain dan rentangnya. Karena peringkat fungsinya R_F Itu sama dengan kodominium R Dapat disimpulkan bahwa:

F: r → R ditentukan oleh garis F (x) = 8 - x adalah fungsi berlebihan.

Ini berlaku untuk semua fungsi linier (fungsi yang tingkat variabelnya lebih besar adalah satu).

Latihan 2

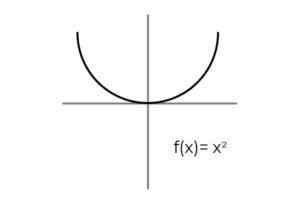
• Mempelajari fungsinya F: r → R didefinisikan oleh F (x) = x² : Tentukan jika itu a fungsi berlebihan. Jika tidak, tunjukkan pengkondisian yang diperlukan untuk membuatnya berlebihan.

Sumber: Penulis

Hal pertama yang perlu dipertimbangkan adalah kodominium F, yang terdiri dari bilangan real R. Tidak ada cara bagi fungsi untuk melempar nilai negatif, yang tidak termasuk yang nyata di antara gambar yang mungkin terjadi.

Mengkondisikan kodominium interval [0 , ∞ ]. Dihindari untuk meninggalkan elemen co -alomio tanpa berhubungan melalui F.

Gambar diulangi untuk pasangan elemen variabel independen, seperti x = 1 Dan x = - 1.  Tapi ini hanya mempengaruhi Injeksi  dari fungsi, tidak menjadi masalah untuk penelitian ini.

Dapat melayani Anda: turunan berturut -turut

Dengan cara ini dapat disimpulkan bahwa:

F: r  →[0, ∞ ) didefinisikan oleh F (x) = x²    Ini adalah fungsi yang terlalu besar

Latihan 3

• Mendefinisikan kondisi kodominasi yang mereka lakukan overjective untuk fungsi

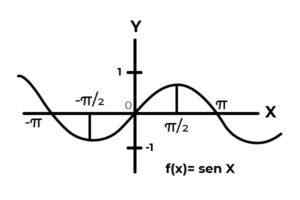
F: r  → R didefinisikan oleh F (x) = sin (x)

F: r  → R didefinisikan oleh F (x) = cos (x)

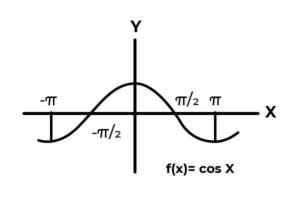Sumber: Penulis Sumber: Penulis.

Perilaku fungsi trigonometri mirip dengan gelombang, karena sangat umum untuk menemukan pengulangan variabel dependen antara gambar. Juga dalam kebanyakan kasus, kisaran fungsi terbatas pada satu atau lebih sektor dari garis nyata.

Ini adalah kasus fungsi sinus dan kosinus. Di mana nilai-nilai mereka berfluktuasi dalam interval [-1, 1]. Interval tersebut harus mengkondisikan kodominasi untuk mencapai amplop fungsi.

F: r  →[ -sebelas ] didefinisikan oleh F (x) = sin (x)  Ini adalah fungsi yang terlalu besar

F: r  →[ -sebelas ]didefinisikan oleh F (x) = cos (x) Ini adalah fungsi yang terlalu besar

Latihan 4

• Mempelajari fungsinya

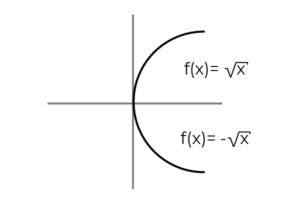
F: [0, ∞ ) → R didefinisikan oleh F (x) = ± √x   menunjukkan apakah itu a fungsi berlebihan

Sumber: Penulis

Fungsinya F (x) = ± √x  Ini memiliki kekhasan yang mendefinisikan 2 variabel dependen pada setiap nilai "x" . Yaitu, rentang menerima 2 elemen untuk masing -masing yang dilakukan di domain. Nilai positif dan negatif untuk setiap nilai "x" harus diverifikasi untuk setiap nilai "x".

Saat mengamati rakitan awal, dicatat bahwa domain telah dibatasi, ini untuk menghindari ketidakpastian yang dihasilkan saat mengevaluasi angka negatif dalam akar torsi akar.

Saat memverifikasi kisaran fungsi, ini menunjukkan bahwa setiap nilai kodominium termasuk dalam kisaran.

Dengan cara ini dapat disimpulkan bahwa:

F: [0, ∞ ) → R didefinisikan oleh F (x) = ± √x  Ini adalah fungsi yang terlalu besar

Dapat melayani Anda: vektor bersamaan: karakteristik, contoh dan latihan

Latihan 4

• Mempelajari fungsinya F (x) = ln x  menunjukkan apakah itu a fungsi berlebihan. Kondisikan set kedatangan dan keberangkatan untuk menyesuaikan fungsi dengan kriteria overjektivitas.

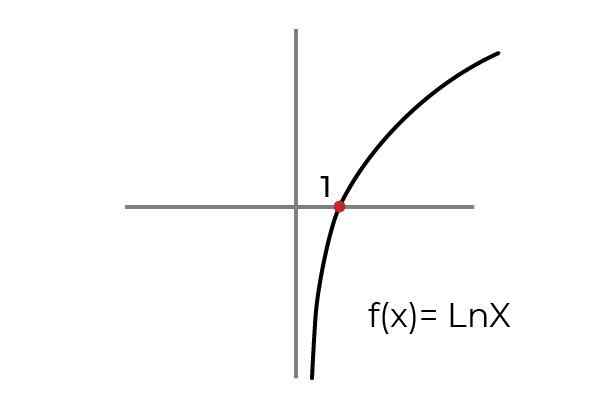Sumber: Penulis

Seperti yang ditunjukkan dalam grafik fungsi F (x) = ln xdidefinisikan untuk nilai "x" lebih besar dari nol. Sedangkan nilai "dan" atau gambar dapat mengambil nilai nyata.

Dengan cara ini kita dapat membatasi domain F (x) = ke interval (0 , ∞ )

Sedangkan peringkat fungsi dapat dipertahankan sebagai set bilangan real R.

Mempertimbangkan ini, dapat disimpulkan bahwa:

F: [0, ∞ ) → R didefinisikan oleh F (x) = ln x  Ini adalah fungsi yang terlalu besar

Latihan 5

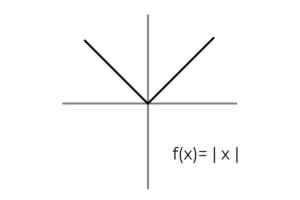
• Mempelajari fungsi nilai absolut F (x) = | x | dan tentukan set kedatangan dan keberangkatan yang dikumpulkan untuk kriteria untuk alegivitas.

Sumber: Penulis

Domain fungsi dipenuhi untuk semua bilangan real R. Dengan cara ini satu -satunya pengkondisian harus dilakukan dalam kodominium, dengan mempertimbangkan bahwa fungsi nilai absolut hanya mengambil nilai positif.

Kodominium fungsi ditetapkan menyamakannya dengan kisaran yang sama

[0 , ∞ )

Sekarang dapat disimpulkan bahwa:

F: [0, ∞ ) → R didefinisikan oleh F (x) = | x |  Ini adalah fungsi yang terlalu besar

Latihan yang diusulkan

1. Verifikasi jika fungsi -fungsi berikut ini berlebihan:

• F: (0, ∞ ) → R didefinisikan oleh F (x) = log (x + 1)
• F: r → R didefinisikan oleh F (x) = x³
• F: r →[1, ∞ )  didefinisikan oleh F (x) = x²  + 1
• [0, ∞ ) → R didefinisikan oleh F (x) = log (2x + 3)
• F: r → R didefinisikan oleh F (x) = dtk x
• F: r - 0 → R didefinisikan oleh F (x) = 1 / x

Referensi

1. Pengantar logika dan pemikiran kritis. Merrilee h. Ikan salmon. Universitas Pittsburgh
2. Masalah dalam analisis matematika. Piotr Bilar, Alfred Witkowski. Universitas Wroclaw. Tiang.
3. Elemen analisis abstrak. Mícheál O'Searcoid PhD. Departemen Matematika. University College Dublin, Beldfield, Dublind 4
4.  Pengantar logika dan metodologi ilmu deduktif. Alfred Tarski, New York Oxford. Oxford University Press.
5.  Prinsip Analisis Matematika. Enrique Linés Escardó. Editorial Reverté s. Hingga 1991. Barcelona, ​​Spanyol.