Fungsi gelar lebih besar dari dua (contoh)

A (polinomial) kelas yang lebih besar dari dua memiliki bentuk umum:

f (x) = a₀ + ke₁x +a₂X² +.. .ke_NX^N

Dengan n = 3, 4, 5, ..., bilangan bulat non -negatif dan koefisien untuk_{salah satu}, ke₁… ke_N, yang biasanya bilangan real.

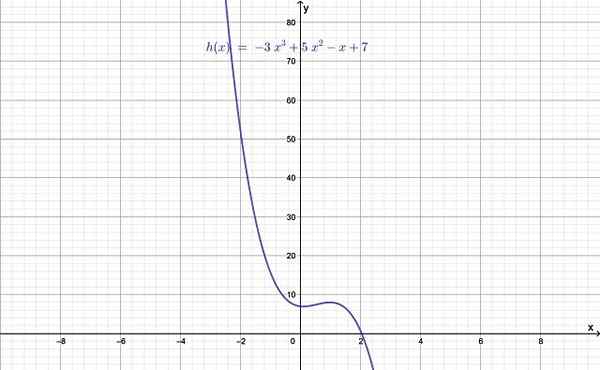Gambar 1.- Grafik fungsi derajat lebih besar dari 2. Sumber: f. Zapata.

Tingkat fungsi diberikan oleh nilai n, yang terbesar dari eksponen dan yang pada gilirannya lebih besar dari 2. Ketika n = 0 adalah fungsi konstan, jika n = 1 itu adalah fungsi linier, dan akhirnya dengan n = 2 itu adalah fungsi kuadratik.

Contoh fungsi lebih dari dua, dalam variabel "x", adalah sebagai berikut:

• f (x) = x³
• H (x) = - 3x³ + 5x² - X + 7
• g (x) = x⁴ - 6x² + 25

Fungsi f (x) = x³ Ini adalah yang paling sederhana dari semua fungsi yang lebih besar dari dua dan derajatnya adalah 3. Gelar 3 juga dikenal sebagai fungsi kubik. Untuk bagiannya, g (x) adalah grade 4, untuk menjadi 4 eksponen maksimum.

Nilai n sangat penting karena menentukan bentuk umum grafik, dan juga jumlah maksimum akar atau persimpangan yang dimiliki fungsi dengan sumbu horizontal. Memang, fungsi 3 -grade akan menyentuh sumbu horizontal paling banyak 3 poin, satu dari kelas 4 akan melakukannya paling banyak dalam 4 poin dan seterusnya.

Adapun istilah independen, dalam fungsi polinomial dari derajat apa pun itu menunjukkan persimpangan fungsi dengan sumbu vertikal.

Karakteristik fungsi polinomial lebih dari dua

Domain

Domain fungsi adalah himpunan nilai yang memungkinkan menghitung nilai y = f (x). Untuk fungsi polinomial set ini adalah angka N nyata, atau set bilangan kompleks, jika perlu untuk memperluas domain.

Dapat melayani Anda: Batas trigonometri: Cara menyelesaikannya, latihan terpecahkan

Berarti, mengingat fungsi polinomial f (x) = a₀ + ke₁x +a₂X² +.. .ke_NX^N, Anda selalu dapat mengganti bilangan real apa pun, melakukan operasi yang ditunjukkan dan memperoleh sebagai akibatnya nilai yal y = f (x) nyata.

Jangkauan

Ini adalah set yang dibentuk oleh semua nilai yang diperoleh f (x), yaitu gambar yang dimiliki setiap nilai x melalui fungsi f (x). Untuk fungsi polinomial yang lebih besar dari 2, set ini adalah bilangan real.

Akar fungsi

Adalah nilai x yang dipenuhi bahwa f (x) = 0. Seperti ditunjukkan di atas, tingkat fungsi menunjukkan jumlah maksimum akar yang dapat dimiliki, meskipun tidak semuanya harus nyata.

Ketika koefisien fungsi adalah bilangan real, akar nyata sesuai dengan persimpangan fungsi dengan sumbu x.

Contoh 1

Akar rasional fungsi f (x) = 2x³ - 9x² + 7x + 6 dapat ditemukan melalui teorema berikut:

Jika akar f (x) = a₀ + ke₁x +a₂X² +.. .ke_NX^N Ini adalah bentuk b/c, sehingga nilai b yang mungkin adalah faktor a_{salah satu} dan nilai -nilai yang mungkin dari C adalah faktor a_N.

Untuk fungsi contoh, kombinasi yang sudah disederhanakan adalah: ± 6, ± 3, ± 2, ± 1, ± 3/2, ± ½. Sekarang masing -masing diuji melalui prosedur divisi sintetis, misalnya. Ketika residu divisi adalah 0, nilai yang terbukti adalah root:

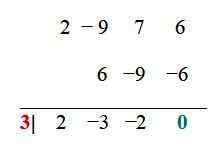
Nilai x₁ = 3 adalah root atau nol fungsi, oleh karena itu (x - 3) adalah faktor umum f (x), dan ini dapat ditulis sebagai:

Ini dapat melayani Anda: Lingkaran Kesatuan: Fungsi dan Aplikasi Trigonometri

f (x) = (x - 3) ∙ (2x² −3x −2)

Dua akar yang tersisa adalah nilai yang memenuhi persamaan 2x² −3x −2 = 0. Persamaan ini dapat diselesaikan melalui rumus umum, kalkulator ilmiah atau mengulangi proses tanteo sebelumnya.

Akar ini x₂ = 2 dan x₃ = - ½, dan sekarang f (x) dapat ditulis sebagai produk dari tiga faktor:

f (x) = (x - 3) ∙ (x - 2) ⋅ (x + ½)

Persimpangan f (x) dengan sumbu x adalah titik: p₁ (3.0), p₂(2.0) dan p₃(−½, 0). Grafik fungsi, yang diperoleh dengan geogebra, menunjukkan persimpangan dengan sumbu x:

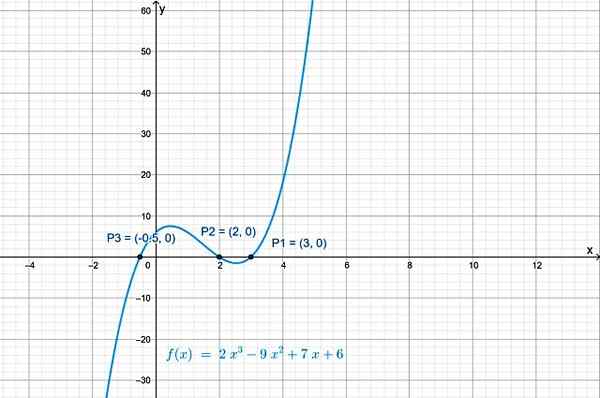Gambar 2.- Fungsi polinomial grade 3 memiliki tiga persimpangan dengan sumbu horizontal. Sumber: f. Zapata.

Persimpangan dengan sumbu vertikal

Untuk menemukan persimpangan fungsi dengan sumbu vertikal, Anda harus menemukan f (0), yang hanya untuk₀.

Contoh 2

Temukan persimpangan f (x) = 2x³ - 9x² + 7x + 6 dengan sumbu vertikal sangat sederhana, saat membuat x = 0 dalam f (x) diperoleh:

f (x) = 6

Dan titik persimpangan fungsi dengan sumbu vertikal adalah p₄(0,6).

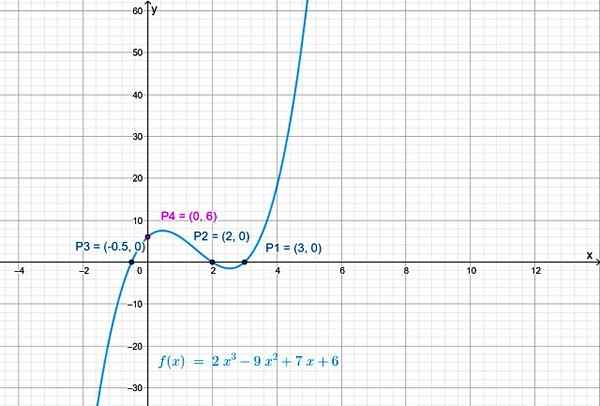Gambar 3. Persimpangan kurva dengan sumbu vertikal membuat x = 0 dalam f (x). Sumber: f. Zapata.

Kontinuitas

Fungsi polinomik secara umum, dan khususnya yang lebih tinggi dari 2 adalah fungsi kontinu di seluruh domain mereka, ini berarti bahwa mereka tidak memiliki lompatan, langkah, lubang atau nilai yang tidak ditentukan oleh mereka. Mereka juga tidak memiliki asimtot, yang vertikal, horizontal atau miring langsung yang mendekati fungsi itu tanpa melintasi mereka.

Kualitas kelembutan dan kontinuitas ini dihargai dalam grafik yang ditunjukkan di atas.

Grafik fungsi lebih tinggi dari 2

Grafik fungsi yang lebih tinggi dari 2 adalah kontinu dan lunak, dan bentuknya tergantung pada tingkat polinomial.

Dapat melayani Anda: permutasi tanpa pengulangan: rumus, demonstrasi, latihan, contoh

Misalnya, orang -orang dari rim grade 3 memiliki tanda negatif dalam istilah dengan tingkat tertinggi).

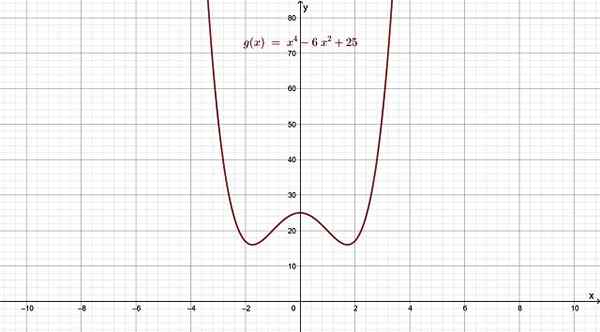Gambar 4. Fungsi poliinomik grade 4, yang grafiknya menyerupai huruf w. Sumber: f. Zapata.

Untuk nilai x jauh dari x = 0, baik kiri maupun kanan, fungsi berperilaku bagaimana istilah tingkat terbesar akan dilakukan, karena ini berlaku di atas orang lain ketika x menjadi sangat besar atau sangat kecil.

Dalam gambar yang mengikuti fungsi f (x) = 2x dibandingkan³ - 9x² + 7x + 6 dengan fungsi r (x) = x³ Dan sangat dihargai bahwa bentuk kedua kurva mirip dengan nilai x yang jauh dari x = 0.

Untuk nilai x besar, fungsi tumbuh dengan cepat dengan cenderung +∞, sedangkan untuk nilai x negatif, fungsi berkurang dengan cepat dan cenderung −∞.

Gambar 5.- Semua fungsi grade n berperilaku sama ketika mereka menjauh dari x = 0, baik kiri maupun kanan. Sumber: f. Zapata.

Membandingkan kurva torsi -kompor (Gambar 4) dengan derajat ganjil (Gambar 2), selama koefisien yang menyertai istilah kelas tertinggi memiliki tanda yang sama, diamati bahwa kurva derajat aneh dimulai dari "y" negatif dan negatif dan negatif Tumbuh, sementara yang dari kelas target dimulai dalam "y" positif dan berkurang.

Referensi

1. Barnett, r. 2000. PRECCCULMENT: Fungsi dan Grafik. 4. Edisi. Bukit McGraw.
2. Perhitungan.Dc. Fungsi polinomik. Pulih dari: perhitungan.Dc.
3. Larson, r. 2012. Prekalkulasi. Ke -8. Edisi. Pembelajaran Cengage.
4. Stewart, J. 2007. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
5. Varsity Tutorrs. Fungsi polinomial grafik. Diperoleh dari: WarsityTorm.com.