Jenis fungsi transenden, definisi, properti, contoh

Itu fungsi transenden Unsur adalah eksponensial, logaritmik, trigonometri, fungsi trigonometri terbalik, hiperbolik hiperbolik dan terbalik. Yaitu, mereka yang tidak dapat diekspresikan dengan polinomial, rasio akar polinomial atau polinomial. 

Fungsi transenden non-elemen juga dikenal sebagai fungsi khusus dan di antaranya fungsi kesalahan dapat dinamai. Itu Fungsi Aljabar (polinomial, quotient polinomial dan akar polinomial) di sebelah fungsi transenden Elemental merupakan apa yang dalam matematika dikenal sebagai fungsi dasar.

Juga dianggap fungsi transenden yang dihasilkan dari operasi antara fungsi transenden atau antara fungsi transenden dan aljabar. Operasi ini adalah: jumlah dan perbedaan fungsi, produk dan rasio fungsi, serta komposisi dua atau lebih fungsi.

[TOC]

Definisi dan Properti

Fungsi eksponensial

Ini adalah fungsi nyata dari variabel independen nyata dari bentuk:

f (x) = a^x = a^X

Di mana ke Itu adalah bilangan real positif (A> 0) diperbaiki disebut pangkalan. Circumflejo atau pengawasan digunakan untuk menunjukkan operasi potensiasi.

Mari kita lakukan untuk berjaga -jaga A = 2 Maka fungsinya seperti ini:

f (x) = 2^x = 2^X

Yang akan dievaluasi untuk beberapa nilai variabel independen x:

Di bawah ini adalah grafik di mana fungsi eksponensial untuk beberapa nilai dasar diwakili, termasuk basis Dan (Nomor Neper Dan ≃ 2.72). Basis Dan Sangat penting bahwa, secara umum, ketika berbicara tentang fungsi eksponensial, Anda pikirkan E^x, itu juga dilambangkan exp (x).

Gambar 1. Fungsi eksponensial a^x, untuk beberapa nilai basis a. (Elaborasi sendiri)

Properti Fungsi Eksponensial

Dari Gambar 1 dapat dilihat bahwa domain fungsi eksponensial adalah bilangan real (dom f = R) dan jangkauan atau rute adalah yang nyata yang nyata (berlari f = R⁺). 

Dapat melayani Anda: simetri

Di sisi lain, terlepas dari nilai basis A, semua fungsi eksponensial melewati titik (0, 1) dan berdasarkan titik (1, a). 

Saat pangkalan A> 1, Kemudian fungsinya tumbuh dan kapan 0 < a < 1 Fungsinya berkurang. 

Kurva y = a^x dan dari y = (1/a)^x  Mereka simetris sehubungan dengan sumbu DAN. 

Dengan pengecualian kasus ini A = 1, Fungsi eksponensial adalah injeksi, yaitu, untuk setiap nilai gambar, satu sesuai dan hanya nilai awal.

Fungsi logaritmik

Ini adalah fungsi aktual nyata dari variabel independen nyata berdasarkan definisi logaritma angka. Berbasis logaritma ke dari angka X, Itu angkanya Dan yang harus diajukan pangkalan untuk mendapatkan argumen X:

catatan_ke(x) = y ⇔ a^y = x

Itu adalah fungsi logaritma di pangkalan ke Ini adalah fungsi terbalik ke fungsi eksponensial berdasarkan ke.

Misalnya:

catatan₂1 = 0, karena 2^0 = 1

Kasus lain, log₂4 = 2, karena 2^2 = 4

Logaritma akar 2 adalah log₂√2 = ½, karena 2^½ = √2

catatan₂ ¼ = -2, dalam tampilan bahwa 2^(-2) = ¼ 

Di bawah ini adalah grafik fungsi logaritma di berbagai basis.

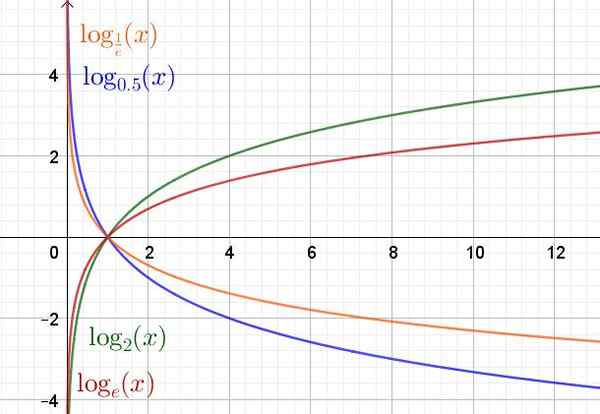Gambar 2. Fungsi eksponensial untuk nilai dasar yang berbeda. (Elaborasi sendiri)

Properti Fungsi Logaritmo

Domain fungsi logaritma dan (x) = logke(X)  Mereka adalah bilangan real yang positif R+. Kisaran atau rute adalah bilangan real R.

Terlepas dari dasarnya, fungsi logaritma selalu melewati titik (1.0) dan titik (a, 1) milik grafik fungsi tersebut.

Itu dapat melayani Anda: teori antrian: sejarah, model, untuk apa dan contohnya

Dalam hal basis A lebih besar dari unit (a> 1) fungsi logaritma meningkat. Tapi ya (0 < a < 1) entonces es una función decreciente.

Fungsi Seno, Coseno dan Tangen

Fungsi sinus memberikan bilangan real dan untuk setiap nilai x, di mana x mewakili ukuran sudut dalam radianes. Untuk mendapatkan nilai sen (x) dari sudut, sudut diwakili dalam lingkaran satuan dan proyeksi sudut tersebut pada sumbu vertikal adalah payudara yang sesuai dengan sudut tersebut.

Di bawah ini adalah (pada Gambar 3) lingkaran trigonometri dan payudara untuk beberapa nilai sudut x1, x2, x3 dan x4.

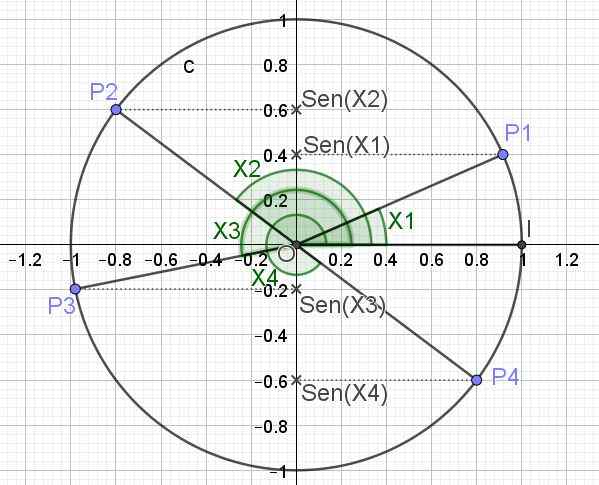Gambar 3. Lingkaran trigonometri dan pangkuan beberapa sudut. (Elaborasi sendiri)

Didefinisikan dengan cara ini nilai maksimum yang dapat dimiliki fungsi sen (x) adalah 1, yang terjadi ketika x = π/2 + 2π n, menjadi n bilangan bulat (0, ± 1, ± 2,). Nilai minimum yang dapat diambil oleh fungsi sen (x) saat x = 3π/2 + 2π n. 

Fungsi coseno y = cos (x) didefinisikan dengan cara yang sama, tetapi proyeksi posisi sudut P1, P2, dll. Dilakukan pada sumbu horizontal dari lingkaran trigonometri.

Di sisi lain, fungsi y = tan (x) adalah rasio antara fungsi sinus dan fungsi kosinus.

Kemudian grafik fungsi transenden sen (x), cos (x) dan tan (x) ditampilkan

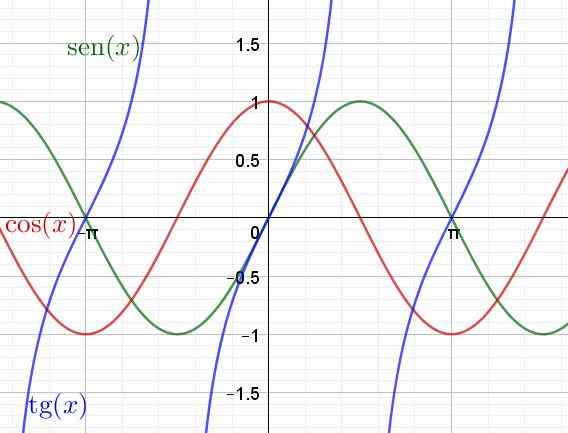Gambar 4. Grafik fungsi transenden, payudara, cosinus dan garis singgung. (Elaborasi sendiri)

Diturunkan dan integral

Berasal dari fungsi eksponensial

Turunannya Dan' dari fungsi eksponensial y = a^x Itu fungsinya a^x dikalikan dengan dia Logaritma Neperian dari pangkalan a:

Dapat melayani Anda: Teori Set: Karakteristik, Elemen, Contoh, Latihan

dan '= (a^x)' = a^x ln a

Dalam kasus tertentu dari pangkalan Dan, Turunan fungsi eksponensial adalah fungsi eksponensial itu sendiri.

Integral dari fungsi eksponensial

Integral yang tidak terbatas a^x Ini adalah fungsi yang dibagi antara logaritma Neperian dari pangkalan. 

Dalam kasus tertentu dari basis E, integral dari fungsi eksponensial adalah fungsi eksponensial itu sendiri.

Tabel turunan dan integral dari fungsi transenden

Di bawah ini adalah tabel ringkasan dari fungsi transenden utama, turunannya dan tidak terbatas (antiderivatif):

Tabel turunan dan integral yang tidak terbatas untuk beberapa fungsi transenden. (Elaborasi sendiri)

Contoh

Contoh 1

Temukan fungsi yang dihasilkan dari komposisi fungsi f (x) = x^3 dengan fungsi g (x) = cos (x):

(f atau g) (x) = f (g (x)) = cos³(X)

Turunannya dan integral yang tidak terbatas adalah:

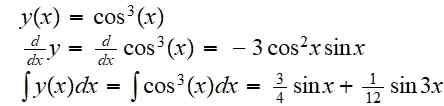
Contoh 2

Temukan komposisi fungsi G dengan fungsi F, menjadi g dan f fungsi yang ditentukan dalam contoh sebelumnya:

(g atau f) (x) = g (f (x)) = cos (x³)

Perlu dicatat bahwa komposisi fungsi bukanlah operasi komutatif.

Turunan dan integral yang tidak terbatas untuk fungsi ini masing -masing:

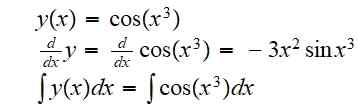
Integral dibiarkan ditunjukkan karena tidak mungkin untuk menulis hasilnya sebagai kombinasi fungsi dasar dengan cara yang tepat.

Referensi

1. Kalkulus variabel tunggal. Ron Larson, Bruce H. Edwards. Pembelajaran Cengage, 10 Nov. 2008
2. Teorema Fungsi Implisit: Sejarah, Teori, dan Aplikasi. Steven G. Krantz, Harold R. Taman. Sains Springer & Media Bisnis, 9 November. 2012
3. Analisis multivariabel. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 Desember. 2010
4. Dinamika Sistem: Pemodelan, Simulasi, dan Kontrol Sistem Mekatronik. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 Mar. 2012
5. Kalkulus: Matematika dan Pemodelan. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 Januari. 1999
6. Wikipedia. Fungsi transenden. Pulih dari: is.Wikipedia.com