Geometri analitik

Kami menjelaskan geometri analitik apa, sejarahnya, studi dan aplikasi apa itu

Apa itu geometri analitik?

Itu geometri analitik Ini adalah cabang matematika di mana geometri dan aljabar digabungkan, untuk menyelesaikan berbagai masalah geometris melalui teknik aljabar.

Gunakan sistem koordinat, seperti sistem koordinat cartesian, yang berutang namanya René Descartes. Dengan cara ini, dimungkinkan untuk mengaitkan kurva di bidang dan di ruang angkasa, dengan persamaan aljabar.

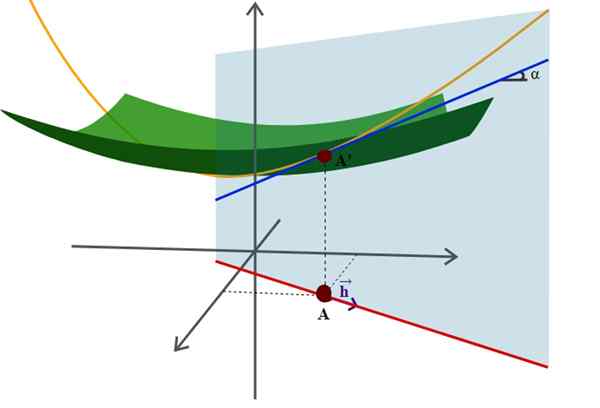
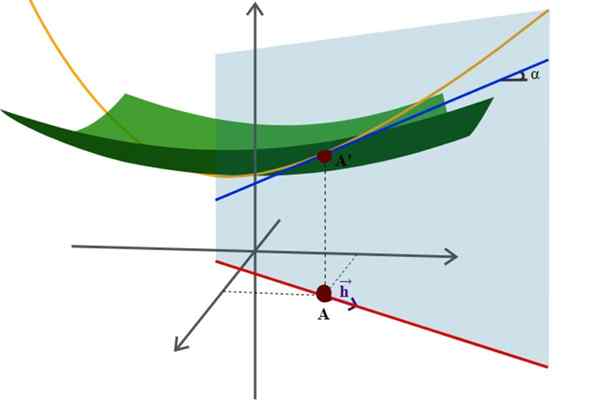Diagram permukaan dalam ruang dan turunan arahnya, salah satu dari banyak aplikasi geometri analitik yang lebih maju. Sumber: Wikimedia Commons.

Contoh dari ini adalah persamaan yang diketahui dengan baik dari jari -jari R -riorsi yang berpusat pada asal sistem koordinat:

Tidak diragukan lagi, dalam banyak kasus lebih sederhana untuk bekerja dengan ekspresi aljabar kurva, daripada dengan representasi geometrisnya sendiri. Ini adalah kasus ketika menghitung persimpangan antara kurva, atau menemukan garis singgung atau pengeringan untuk mereka.

Demikian pula, melalui geometri analitik, dimungkinkan untuk fungsi tata letak grafik. Dan seperti yang diketahui, fungsi memungkinkan pemodelan sains dan masalah teknik. Oleh karena itu, geometri analitik hadir dalam kurikulum karier yang terkait dengan bidang pengetahuan ini.

Sejarah Singkat Geometri Analitik

Geometri analitik berawal dari paruh pertama abad ke-17, dengan tangan dua ahli matematika Prancis terkenal: René Descartes (1596-1650) dan Pierre de Fermat (1601-1665).

Rene Descartes

Namun, dapat dikatakan bahwa latar belakangnya tanggal berabad-abad yang lalu, kepada ahli matematika Yunani Apollonius dari Pergamo (262-190 a.C.). Dia menulis risalah tentang kerucut, yang dia berikan nama mereka: keliling, elips, perumpamaan dan hiperbola.

Itu dapat melayani Anda: proporsionalitas majemuk: penjelasan, tiga aturan majemuk, latihan

Dengan demikian, karya Apollonio adalah dasar bagi, jauh kemudian, Prancis René Descartes dan Pierre de Fermat meletakkan dasar -dasar geometri analitik, secara mandiri. Tapi Descartes dianggap sebagai bapak sains ini, karena dia adalah orang pertama yang mempublikasikan karyanya.

Descartes, Fermat dan Euler

Dalam pidato metode 1637, Descartes menyatukan dua disiplin ilmu bahwa sampai saat itu telah dipisahkan: aljabar dan geometri. Dalam karyanya, Descartes memperkenalkan sistem koordinat Cartesian, untuk menemukan titik di pesawat dan di luar angkasa.

Ini juga memanfaatkan persamaan aljabar -kedua dengan dua variabel, untuk menggambarkan bagian kerucut dan didedikasikan untuk memecahkan masalah geometris dengan mereka. Juga untuk membuat bagian yang baik dari notasi matematika yang saat ini digunakan.

Pierre de Fermat lebih terkait dengan optik daripada dengan geometri analitik, namun, kontribusinya penting.

Pada tahun 1629, Fermat melanjutkan kerucut Apollonius dari Pergamo dan menciptakan teknik -teknik yang membentuk geometri analitik, menciptakan sistem koordinatnya sendiri dan dengan jelas mendefinisikan konsep kunci dari Tempat geometris, dengan mana studi geometri analitik dimulai.

Namun, karya -karya Fermat tidak melihat cahaya sampai 1679, diterbitkan oleh putranya, ketika ahli matematika sudah mati. Untuk alasan ini, ayah geometri analitik disebabkan oleh descartes.

Selanjutnya untuk matematikawan Prancis, Swiss Leonardo Euler (1707-1783) menetapkan basis formal geometri analitik. Euler memperkenalkan beberapa sistem koordinat di bidang dan ruang: koordinat persegi panjang, kutub dan miring, serta transformasi dari satu sistem ke sistem lainnya.

Dapat melayani Anda: bagaimana informasi yang diperoleh dalam survei?

Dalam karya -karyanya tentang geometri analitik, Euler juga memperdalam klasifikasi berbagai kurva, sesuai dengan tingkat persamaan aljabar yang representatif (urutan ketiga dan keempat) dan mempelajari sifat -sifatnya secara intensif, persamaan garis singgung, kelengkungan, simetri dan banyak lagi.

Apa yang mempelajari geometri analitik?

Secara umum, geometri analitik berfokus pada studi elemen geometris, seperti titik, segmen, garis, kurva, permukaan dan volume. Untuk melakukan ini, seperti yang dinyatakan di atas, ia menetapkan persamaan aljabar yang menggambarkan dan menghubungkan elemen -elemen ini, memungkinkan manajemen mereka melalui teknik aljabar.

Tujuan utama geometri analitik, dengan cara yang sangat ringkasan, adalah sebagai berikut:

1. Menetapkan sistem koordinat cartesian dan sistem koordinat kutub, untuk menemukan titik di pesawat, serta perpanjangannya ke titik di luar angkasa.
2. Gambar segmen, lurus, kurva dan permukaan di bidang dan ruang cartesian.
3. Menyimpulkan persamaan yang secara analitis menggambarkan kurva dan konstruksi pada bidang dan/atau ruang, serta studi tentang semua sifatnya.
4. Klasifikasi kurva, permukaan dan volume.
5. Turunkan formula mendasar untuk memecahkan masalah pada titik -titik penting, lurus, rencana, sudut, paralelisme, tegak lurus, jarak, persimpangan, area dan banyak lagi.
6. Memecahkan masalah geometris melalui penerapan metode aljabar, yang rumusnya merujuk pada titik -titik penting, persamaan untuk garis, rencana, sudut, jarak antara titik, antara garis dan titik, titik tangency, garis kering, area, area dan banyak lagi lainnya.
7. Bekerja dengan ruang vektor dan produk antar vektor.

Jarak antara dua titik

Sebagai contoh dari berbagai aplikasi geometri analitik, salah satu yang paling sederhana adalah perhitungan jarak antara dua titik bidang. Adalah dua poin p₁ Dan p₂, koordinat (x₁,Dan₁) dan (x₂,Dan₂) masing -masing, jarak D di antara mereka dihitung oleh:

Dapat melayani Anda: trinomial

Koordinat Kutub

Titik bidang dapat ditentukan melalui jarak "R" ke asal sistem koordinat, yang disebut polo, dan sudut yang membentuk garis yang berisi titik dan tiang, dengan sumbu horizontal atau sumbu kutub.

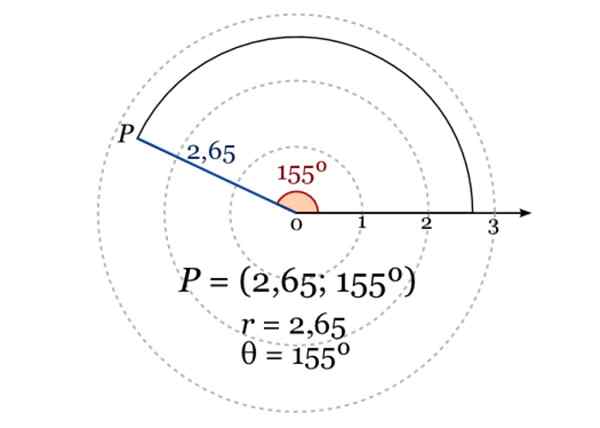Gambar menunjukkan koordinat kutub titik P, di mana r = 2.65 dan sudut dalam derajat sehubungan dengan sumbu kutub adalah 155º. Sumber: Wikimedia Commons.

Aplikasi Geometri Analitik

Fondasi perhitungan infinitesimal

Geometri analitik sangat penting untuk pengembangan perhitungan infinitesimal, karena memfasilitasi representasi grafik kurva dan fungsi, dan bekerja dengannya dengan cara analitik, untuk membuat model yang mewakili fenomena alam.

Peta

Sistem koordinat cartesian membantu membuat peta dan mengidentifikasi tempat melalui garis lintang dan panjang, setara dengan koordinat cartesian titik di pesawat.

Perhitungan topografi

Berbagai jenis sistem koordinat digunakan dalam topografi dan merupakan dasar dari studi dan aplikasi mereka. Di antara mereka adalah sistem koordinat kutub yang dijelaskan di atas.

Lintasan benda selestial

Bagian kerucut, yang dijelaskan melalui geometri analitik, berpartisipasi dalam fenomena penting alam, seperti lintasan benda -benda selestial, tunduk pada gaya gravitasi. Misalnya, planet dan beberapa komet menggambarkan lintasan elips di sekitar matahari, dengan ini terletak di salah satu lampu sorot.

Arsitektur dan Konstruksi Sipil

Banyak kurva adalah bagian dari konstruksi arsitektur, misalnya, kabel jembatan gantung dapat berupa perumpamaan.

Sistem Penentuan posisi Global

Sistem penentuan posisi global atau GPS memungkinkan lokasi yang mungkin dengan presisi, serta benda bergerak, seperti kendaraan dan kapal. Ini juga membantu orang menjadi lebih mudah ke tujuan mereka, membimbing mereka di rute terbaik.