Tingkat polinomial bagaimana hal itu ditentukan, contoh dan latihan

Dia tingkat polinomial di dalam A Variabel diberikan oleh istilah yang dimiliki eksponen utama, dan jika polinomial memiliki dua atau lebih variabel, Maka derajat ditentukan oleh jumlah eksponen dari setiap istilah, jumlah utama makhluk polinomial.

Mari kita lihat bagaimana menentukan tingkat polinomial secara praktis.

Gambar 1. Persamaan Einstein yang terkenal untuk energi E adalah monomial kelas 1 absolut untuk variabel massa, yang dilambangkan dengan M, karena kecepatan cahaya C dianggap konstan. Sumber: Piqsels.

Misalkan polinomial p (x) = -5x + 8x³ + 7 - 4x². Polinomial ini adalah variabel, dalam hal ini adalah variabel X. Polinomial ini terdiri dari beberapa istilah, yang merupakan sebagai berikut:

-5x; 8x³; 7; - 4x²

 Mari Pilih dari Empat istilah yang eksponennya lebih besar, istilah ini adalah:

8x³

Dan sekarang apa eksponennya? Jawabannya adalah 3. Oleh karena itu p (x) adalah polinomial grade 3.

Jika polinomial yang dimaksud memiliki lebih dari satu variabel, maka derajatnya dapat:

-Mutlak

-Dalam kaitannya dengan variabel

Gelar absolut dijelaskan di awal: menambahkan eksponen dari setiap istilah dan memilih yang terhebat.

Di sisi lain, tingkat polinomial sehubungan dengan salah satu variabel atau huruf, adalah nilai terbesar dari eksponen yang mengatakan surat tersebut. Intinya akan lebih jelas dengan contoh dan latihan yang diselesaikan dari bagian berikut.

[TOC]

Contoh nilai polinomial

Polinomial dapat diklasifikasikan berdasarkan gelar, dapat menjadi gelar pertama, kelas dua, kelas tiga dan sebagainya. Untuk contoh Gambar 1, energi adalah monomial -degree pertama untuk massa.

Dapat melayani Anda: kongruensi: angka kongruen, kriteria, contoh, latihan

Penting juga untuk mengamati bahwa jumlah istilah yang dimiliki polinomial sama dengan derajat ditambah 1. Jadi:

-Polinomial tingkat pertama memiliki 2 istilah: a₁x + a_{salah satu}

-Polinomial Degree kedua memiliki 3 istilah: a₂X² + ke₁x + a_{salah satu}

-Polinomial tingkat ketiga memiliki 4 istilah: a₃X³ + ke₂X² + ke₁x + a_{salah satu}

Dan seterusnya. Pembaca yang penuh perhatian akan mengamati bahwa polinomial dari contoh -contoh sebelumnya ditulis dengan cara yang menurun, yaitu, pertama -tama menempatkan istilah dengan gelar utama.

Berbagai polinomial muncul di tabel berikut, baik dari satu dan beberapa variabel dan derajat absolut masing -masing:

Tabel 1. Contoh polinomial dan gelar mereka

Polinomial	Derajat
3x4+5x3-2x+3	4
7x3-2x2+3x-6	3
6	0
X-1	1
X5-bx4+Abx3+AB3X2	6
3x3Dan5 + 5x2Dan4 - 7xy2 + 6	8

Dua polinomial terakhir memiliki lebih dari satu variabel. Istilah yang memiliki gelar absolut terbesar telah menonjol dalam tebal, sehingga pembaca dengan cepat memeriksa gelar. Penting untuk diingat bahwa ketika variabel tidak memiliki eksponen tertulis, dapat dipahami bahwa eksponen tersebut sama dengan 1.

Misalnya dalam istilah yang menonjol AB³X² Ada tiga variabel, yaitu: ke, B Dan X. Dalam istilah itu, ke Diangkat menjadi 1, yaitu:

a = a¹

Karena itu AB³X² = a¹B³X²

Karena eksponen B adalah 3 dan dari x adalah 2, segera diikuti bahwa tingkat istilah ini adalah:

1+3+2 = 6

Dan itu adalah tingkat absolut polinomial, karena tidak ada istilah lain yang memiliki gelar yang lebih besar.

Prosedur untuk bekerja dengan polinomial

Saat bekerja dengan polinomial, penting untuk memperhatikan tingkat yang sama, karena di tempat pertama dan sebelum melakukan operasi apa pun, lebih mudah untuk mengikuti langkah -langkah ini, di mana gelar memberikan informasi yang sangat penting:

-Pesan preferensi polinomial dalam arti yang menurun. Dengan cara ini, istilah dengan nilai tertinggi ada di sebelah kiri dan yang terendah ke kanan.

Dapat melayani Anda: endecagon

-Kurangi istilah yang serupa, prosedur yang terdiri dari menambahkan semua istilah variabel yang sama dan derajat yang ada dalam ekspresi aljabar secara aljabar.

-Jika perlu, polinomial selesai, diselingi istilah yang koefisiennya adalah 0, dalam hal persyaratan dengan beberapa eksponen.

Memesan, mengurangi dan menyelesaikan polinomial

Diberikan polinomial P (x) = 6x² - 5x⁴- 2x+3x+7+2x⁵  - 3x³ + X⁷ -12 Ini diminta untuk memesannya secara berkurang, mengurangi persyaratan yang sama jika ada dan menyelesaikan persyaratan yang hilang karena akurat.

Hal pertama yang harus dicari adalah istilah dengan eksponen utama, yaitu tingkat polinomial, yang ternyata:

X⁷

Oleh karena itu p (x) adalah kelas 7. Kemudian polinomial diperintahkan, dimulai dengan istilah ini di sebelah kiri:

P (x) = x⁷ + 2x⁵ - 5x⁴ - 3x³ + 6x² - 2x+3x+7 -12

Istilah serupa sekarang dikurangi, yang merupakan berikut: - 2x dan 3x di satu sisi. Dan 7 dan -12 di sisi lain. Untuk menguranginya, koefisien ditambahkan secara aljabar dan variabel dibiarkan tidak berubah (jika variabel tidak muncul di sebelah koefisien, harus diingat bahwa x⁰ = 1):

-2x+3x = x

7 -12 = -5

Hasil ini diganti dalam p (x):

P (x) = x⁷ +2x⁵ - 5x⁴ - 3x³ + 6x² + x -5

Dan akhirnya polinomial diperiksa untuk melihat apakah suatu eksponen hilang dan berlaku, sebuah istilah yang eksponennya 6 tidak ada, oleh karena itu selesai dengan nol seperti ini:

P (x) = x⁷ + 0x⁶ +2x⁵ - 5x⁴ - 3x³ + 6x² + X - 5

Sekarang diamati bahwa polinomial dibiarkan dengan 8 istilah, karena seperti yang dikatakan sebelumnya, jumlah istilah sama dengan derajat + 1.

Pentingnya tingkat polinomial dalam jumlah dan pengurangan

Dengan polinomial, operasi dan operasi pengurangan dapat dilakukan, di mana hanya istilah serupa yang ditambahkan atau dikurangi, yang merupakan variabel yang sama dan derajat yang sama. Jika tidak ada istilah yang serupa, jumlah atau pengurangan dibiarkan ditunjukkan secara sederhana.

Dapat melayani Anda: properti distributif

Setelah jumlah atau pengurangan telah dilakukan, yang terakhir menjadi jumlah yang berlawanan, tingkat polinomial yang dihasilkan selalu sama dengan atau kurang dari tingkat penambahan polinomial yang lebih besar.

Latihan terpecahkan

- Latihan diselesaikan 1

Temukan jumlah berikut dan tentukan gelar absolutnya:

ke³- 8ax²  + X³ + Ke -5²X - 6ax² - X³ + 3³ - Ke -5²x - x³ + ke³+ 14ax² - X³

Larutan

Ini adalah polinomial dari dua variabel, sehingga lebih mudah untuk mengurangi istilah yang sama:

ke³- 8ax²  + X³ + Ke -5²X - 6ax² - X³ + 3³ - Ke -5²x - x³ + ke³+ 14ax² - X³ =

= a³ + 3³ + ke³ - 8ax² - 6ax²+ 14ax² +Ke -5²X - 5a²x+ x³- X³- X³- X³ =

= 5a³ - 2x³

Kedua istilah adalah grade 3 di setiap variabel. Oleh karena itu tingkat absolut polinomial adalah 3.

- Latihan diselesaikan 2

Ekspresikan sebagai polinomial luas gambar geometris datar berikut (Gambar 2 kiri). Berapa tingkat polinomial yang dihasilkan?

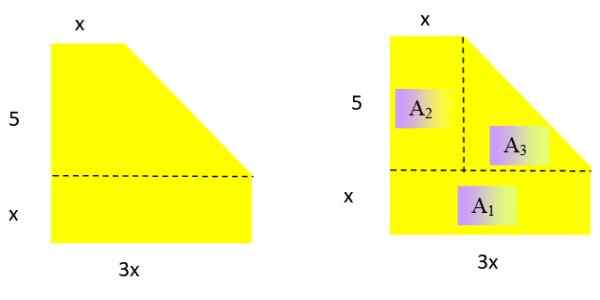Gambar 2. Di sebelah kiri, angka untuk tahun ini menyelesaikan 2 dan ke kanan, sosok yang sama terurai di tiga area yang ekspresinya diketahui. Sumber: f. Zapata.

Larutan

Menjadi suatu daerah, polinomial yang dihasilkan harus kelas 2 dalam variabel x. Untuk menentukan ekspresi yang memadai untuk area tersebut, gambar tersebut dipecah menjadi area yang diketahui:

Area persegi panjang dan segitiga masing -masing: Dasar X Tinggi Dan Basis x tinggi /2

KE₁ = x . 3x = 3x²; KE₂ = 5 . x = 5x; KE₃ = 5 . (2x /2) = 5x

Catatan: Basis segitiga adalah 3x - x = 2x dan tingginya 5.

Sekarang tiga ekspresi yang diperoleh ditambahkan, dengan ini Anda memiliki luas gambar tergantung pada X:

3x² + 5x + 5x = 3x² + 10x

Referensi

1. Baldor, a. 1974. Aljabar Dasar. Budaya Venezuela S.KE.
2. Jiménez, r. 2008. Aljabar. Prentice Hall.
3. Wikilibros. Polinomial. Pulih dari: is. Wikibooks.org.
4. Wikipedia. Kelas (polinomial). Pulih dari: is.Wikipedia.org.
5. Zill, d. 1984. Aljabar dan Trigonometri. Mac Graw Hill.