Definisi hypercubo, dimensi, koordinat, dibuka

A Hypercubo adalah dimensi kubus n. Kasus hypercubo dimensi tertentu disebut Testeract. Hypercubo atau N-cubo terdiri dari segmen lurus, semua dengan panjang yang sama yang ortogonal dalam simpulnya.

Manusia merasakan ruang tiga dimensi: lebar, tinggi dan dalam, tetapi tidak mungkin bagi kita untuk memvisualisasikan hypercubo dimensi yang lebih besar dari 3. 

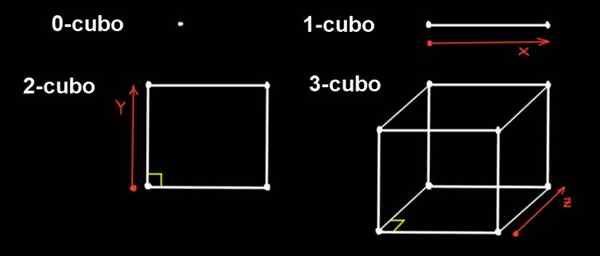
Gambar 1. 0-cubo adalah titik, jika titik itu memanjang dalam satu arah jarak dengan cara 1-cubo, jika 1-cubo itu memanjang jarak ke arah ortogonal ada 2-cubo (dari sisi ke x a), Jika 2-cubo memanjang jarak ke arah ortogonal ada 3-cubo. Sumber: f. Zapata.

Kita dapat membuat proyeksi dalam ruang tiga dimensi untuk mewakilinya, mirip dengan bagaimana kita memproyeksikan kubus di pesawat untuk mewakilinya.

Di dimensi 0 satu-satunya gambar adalah intinya, jadi 0-cubo adalah suatu titik. 1-cubo adalah segmen lurus, yang dibentuk dengan menggerakkan titik di kejauhan.

Untuk bagiannya 2-cubo adalah persegi. Itu dibangun dengan menggusur 1-cubo (segmen panjang a) ke arah dan, yang ortogonal ke alamat x, jarak ke.

3-cubo adalah kubus umum. Itu dibangun dari persegi yang menggusur yang sama di arah ketiga (z), yang ortogonal ke arah x dan y, jarak ke.

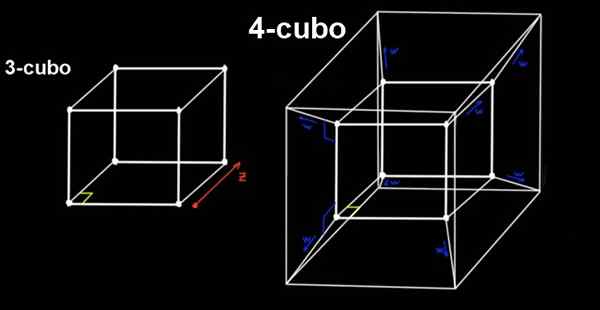Gambar 2. 4-cubo (testeract) adalah perpanjangan dari 3-cubo dalam arah ortogonal ke tiga alamat spasial konvensional. Sumber: f. Zapata.

4-cubo adalah uji coba, yang dibangun dari 3-cubo menggusur ortogonal yang sama, jauh ke, Menuju dimensi keempat (atau arah keempat), yang tidak dapat kita rasakan.

Pemicu memiliki semua sudut lurus, ia memiliki 16 simpul dan semua tepi (total 18) memiliki panjang yang sama ke.

Jika panjang tepi N-cubo atau hypercubo dimensi N adalah 1, maka itu adalah unit hypercubo, di mana ukuran diagonal terpanjang √n.

Dapat melayani Anda: pemrograman linier: untuk apa, model, pembatasan, aplikasiGambar 3. N-Cubo diperoleh dari (N-1) -Cubo yang memperluasnya secara ortogonal di dimensi berikutnya. Sumber: Wikimedia Commons.

[TOC]

Apa dimensinya?

Dimensi adalah tingkat kebebasan, atau arah yang mungkin di mana suatu objek dapat bergerak.

Di dimensi 0 tidak ada kemungkinan untuk bergerak dan satu -satunya objek geometris yang mungkin adalah intinya.

Dimensi dalam ruang Euclidian diwakili oleh garis berorientasi atau sumbu yang mendefinisikan dimensi itu, yang disebut sumbu x. Pemisahan antara dua titik A dan B adalah jarak Euclidian:

D = √ [(x_ke - X_B)²]. 

Dalam dua dimensi, ruang diwakili oleh dua garis berorientasi ortogonal satu sama lain, disebut x dan sumbu.

Posisi titik mana pun dalam ruang dua -dimensi ini diberikan oleh sepasang koordinat Cartesian (x, y) dan jarak antara dua titik A dan B apa saja akan:

D = √ [(x_ke - X_B)² + (Dan_ke - Dan_B)²]

Karena itu adalah ruang di mana geometri euclid terpenuhi.

Ruang tiga dimensi

Ruang tiga dimensi adalah ruang di mana kita bergerak. Ini memiliki tiga arah: lebar, tinggi dan dalam.

Di ruangan kosong, sudut tegak lurus satu sama lain memberikan ketiga arah ini dan untuk masing -masing kita dapat mengaitkan sumbu: x, y, z.

Ruang ini juga Euclidian dan jarak antara dua titik A dan B dihitung sebagai berikut:

D = √ [(x_ke - X_B)² + (Dan_ke - Dan_B)² + (z_ke - z_B)²]

Manusia tidak dapat merasakan lebih dari tiga dimensi spasial (atau euclideas).

Namun, dari sudut pandang matematika yang ketat itu mungkin.

Di ruang ini titik memiliki koordinat: (x1, x2, x3, ..., xn) dan jarak antara dua titik adalah: 

D = √ [(x_1st - X_{1 b})² + (X_2nd - X_2b)² +... + (x_na - X_NB)²].

Dapat melayani Anda: Distribusi Hypergeometrik: Rumus, Persamaan, Model

Dimensi dan waktu keempat

Memang, dalam teori waktu relativitas diperlakukan sebagai satu dimensi lagi dan koordinat terkait.

Tetapi harus diklarifikasi bahwa koordinat yang terkait dengan waktu ini adalah angka imajiner. Oleh karena itu pemisahan dua titik atau peristiwa dalam ruang-waktu bukanlah Euclidiana, tetapi mengikuti metrik Lorentz.

Hypercubo empat dimensi (pemicu) tidak hidup dalam ruang-waktu, milik euclideal hyper-space empat dimensi. 

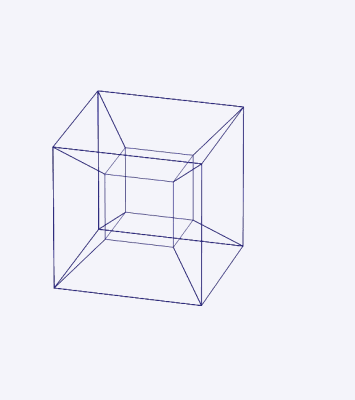
Gambar 4. Proyeksi 3D dari hypercubo empat dimensi dalam rotasi sederhana di sekitar bidang yang membagi sosok depan ke kiri, kembali ke kanan dan dari atas ke bawah. Sumber: Wikimedia Commons.

Koordinat hypercubo

Koordinat simpul-simpul N-Cubo yang berpusat pada asal dicapai dengan membuat semua permutasi yang mungkin dari ekspresi berikut:

(A/2) (± 1, ± 1, ± 1, .. ., ± 1)

Dimana a adalah panjang tepi.

-Dia volume Dari tepi tepi A adalah: (A/2)^N (2^N) = a^N.

-Itu Diagonal terpanjang Itu adalah jarak antara simpul yang berlawanan.

-Berikut ini simpul yang berlawanan di persegi: (-1, -1) dan (+1, +1).

-Dan dalam a kubus: (-1, -1, -1) dan (+1, +1, +1). 

-Itu Diagonal terpanjang Tindakan N-Cubo: 

D = √ [1 -(-1))² +... + (1 -(-1))²] = √ [n 2²] = 2√n

Dalam hal ini diasumsikan bahwa sisi adalah A = 2. Untuk sisi N-cubo kepada siapa pun akan tetap:

d = A√n.

-Percobaan memiliki masing -masing dari 16 simpulnya yang terhubung ke empat tepi. Gambar berikut menunjukkan bagaimana simpul terhubung dalam pemicu.

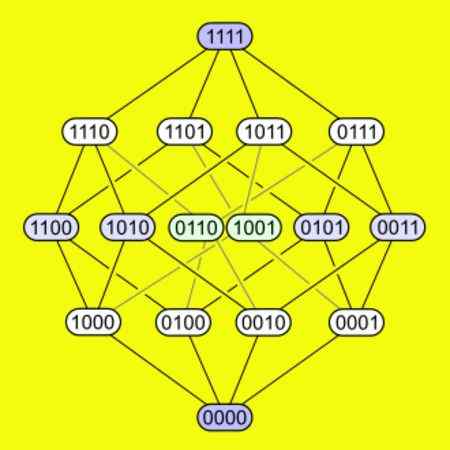Gambar 5. 16 simpul hypercubo empat dimensi ditampilkan dan bagaimana mereka menghubungkan hal yang sama. Sumber: Wikimedia Commons.

Terungkap dari hypercubo

Sosok geometris biasa, misalnya polyhedron, dapat dibuka dalam beberapa angka dimensi yang lebih rendah.

Dalam kasus 2-cubo (persegi) dapat dibuka dalam empat segmen, yaitu empat 1-cubo.

Ini dapat melayani Anda: Distribusi Poisson: Rumus, Persamaan, Model, Properties

Demikian pula 3-cubo dapat dibuka dalam enam 2-cubo.

Gambar 6. N-Cubo dapat dibuka di beberapa (N-1) -Cubos. Sumber: Wikimedia Commons.

4-cubo (testeract) dapat dibuka dalam delapan 3-cubo.

Animasi berikut menunjukkan pembukaan babat.

Gambar 7. Hypercubo 4 -dimensi dapat dibuka dalam delapan kubus tiga dimensi. Sumber: Wikimedia Commons. Angka 8. Proyeksi tiga dimensi dari hypercubo empat dimensi membuat rotasi ganda di sekitar dua bidang ortogonal. Sumber: Wikimedia Commons.

Referensi

1. Budaya Ilmiah. Hypercubo, memvisualisasikan dimensi keempat. Diperoleh dari: CulturAcientifica.com
2. Epsilones. Hypercubo atau Tesseract tetradimensional. Pulih dari: epsilones.com
3. Perez R, Aguilera A. Metode untuk mendapatkan uji coba dari pengembangan hypercubo (4D). Pulih dari: risetgate.bersih
4. Wikilibros. Matematika, polyhedra, hypercubes. Pulih dari: is.Wikibooks.org
5. Wikipedia.  Hypercube. Diperoleh dari: di.Wikipedia.com
6. Wikipedia. Tesseract. Diperoleh dari: di.Wikipedia.com