Hiperbola

Apa itu hiperbola?

Hiperbola adalah himpunan titik bidang sedemikian rupa sehingga nilai absolut dari perbedaan antara jarak ke dua titik tetap, yang disebut lampu sorot, tetap konstan. Set titik ini membentuk kurva dengan dua cabang yang diamati pada Gambar 1.

Ada titik p (x, y), fokus f₁ dan f₂ memisahkan jarak yang sama dengan 2c. Cara matematika untuk mengekspresikan hubungan ini adalah melalui:

Gambar 1. Hiperbola dengan sumbu fokus horizontal. Sumber: f. Zapata.

Semua titik hiperbola memenuhi kondisi ini, yang mengarah ke persamaan hiperbola, seperti yang akan dilihat nanti. Titik tengah antara lampu sorot disebut pusat C dan dalam gambar itu bertepatan dengan titik (0,0), tetapi hiperbola juga dapat dipindahkan dan pusatnya sesuai dengan titik koordinat lain C (h, k).

Pada gambar atas, sumbu x adalah sumbu fokus hiperbola, karena ada lampu sorot, tetapi Anda juga dapat membangun satu yang sumbu fokusnya adalah sumbu dan sumbu.

Hiperbola adalah bagian dari kurva yang dikenal sebagai berbentuk kerucut, Mereka disebut itu karena mereka dapat berasal dari potongan kerucut dengan bagian datar. Hiperbola diperoleh saat memotong kerucut dan bidang, asalkan tidak melewati titik kerucut dan sudut yang membentuk bidang dengan sumbu kerucut kurang dari yang terbentuk dengan sumbu generatrix dari sama.

Bersama dengan perumpamaan, keliling dan elips, kerucut diketahui sejak zaman kuno. Matematikawan Yunani Apollonius dari Perga (262-190 SM) menulis perjanjian geometri di mana ia merinci propertinya dan ia sendiri memberi mereka nama-nama yang mereka kenal satu sama lain sampai hari ini.

Karakteristik hiperbola

Ini adalah beberapa karakteristik hiperbola yang paling menonjol:

1. Ini adalah kurva datar, oleh karena itu cukup untuk memberikan koordinat (x, y) dari setiap titik yang menjadi miliknya.
2. Itu juga kurva terbuka, tidak seperti keliling atau elips.
3. Ini memiliki dua cabang yang disusun secara simetris.
4. Baik sumbu vertikal dan sumbu horizontal dapat dianggap sebagai sumbu simetri, tetapi sumbu di mana lampu sorot disebut sumbu fokus atau sumbu utama.
5. Itu simetris sehubungan dengan pusatnya.
6. Hiperbola memotong sumbu fokus pada dua titik yang disebut Sudut, Itulah sebabnya sumbu fokus kadang -kadang disebut Sumbu nyata, sedangkan sumbu lainnya dipanggil Sumbu imajiner, Karena tidak memiliki poin yang sama dengan hiperbola.
7. Pusat hiperbola terletak di tengah -tengah di antara titik -titik yang disebut fokus.
8. Ini terkait dengan dua baris yang sangat khusus yang disebut asimtot, yang merupakan garis yang didekati hiperbola, tetapi tanpa melintasi mereka, ketika nilai -nilai x e y sangat besar. Asimtot berpotongan di tengah hiperbola.

Dapat melayani Anda: Fungsi Overjektif: Definisi, Properti, Contoh

Persamaan dan Rumus

Persamaan HiPerbol dengan pusat di (0,0)

Mulai dari definisi yang diberikan di awal:

Untuk konstanta positif ini, biasanya disebut 2a dan jarak yang memisahkan simpul hiperbola, lalu:

Di sisi lain, DP₁, Dp₂ dan 2c adalah sisi segitiga yang ditunjukkan pada Gambar 1, dan dengan geometri dasar, pengurangan kotak sisi segitiga selalu kurang dari kuadrat dari sisi yang tersisa. Jadi:

4² < 4c²

DAN:

ke < c

Hasil ini akan segera berguna.

Sebagai jarak antara dua titik p₁(X₁,Dan₁) Dan p₂(X₂,Dan₂) adalah:

Dengan mengganti koordinat p (x, y), f₁(-C, 0) dan f₂(C, 0) tetap:

Yang setara dengan:

Kotak di kedua anggota untuk menghilangkan akar dan mengatur ulang istilah yang Anda capai:

Kuantitas c² - ke², yang selalu menjadi jumlah yang positif karena < c, se la denomina b², Oleh karena itu di atas ditulis ulang sebagai:

B²X² - ke²Dan² = a² B²

Membagi semua istilah dengan² B², Ini adalah persamaan hiperbola yang berpusat pada (0,0) dengan sumbu nyata horizontal:

Dengan A dan B lebih besar dari 0. Persamaan ini disebut Persamaan Canonical Hyerbola dan penyebutnya² Itu selalu sesuai dengan fraksi positif.

Hiperbola berpusat pada (0,0) dan dengan sumbu nyata vertikal mengambil bentuk:

Persimpangan hiperbola dengan sumbu koordinat

Persimpangan hiperbola dengan sumbu koordinat sedang dilakukan masing -masing y = 0 dan x = 0 dalam persamaan:

Untuk y = 0

X² /ke² = 1 ⇒ x² = a²

x = ± a

Hiperbola memotong ke sumbu x dalam dua titik yang disebut simpul, yang koordinatnya masing -masing adalah: x = a y x = -a

Untuk x = 0

Itu diperoleh -dan² /B² = 1, yang tidak memiliki solusi nyata dan mengikuti bahwa hiperbola tidak memotong ke sumbu vertikal.

Persamaan hiperbola dengan pusat di (h, k)

Jika pusat hiperbola berada pada titik C (h, k), maka persamaan kanoniknya adalah:

Elemen Hiperbola

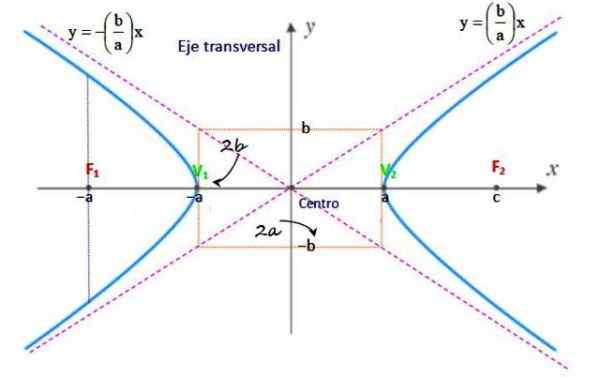Gambar 2. Elemen Hiperbola. Sumber: f. Zapata.

Tengah

Itu adalah titik tengah segmen f₁F₂ Dan koordinatnya adalah (h, k) atau (x_{salah satu},Dan_{salah satu}).

Dapat melayani Anda: Divisi sintetis

Fokus

Mereka adalah dua titik tetap f₁ dan f₂ yang ada pada sumbu nyata hiperbola, sehubungan dengan perbedaan jarak ke titik p (x, y) tetap konstan. Jarak antara lampu sorot dan pusat hiperbola adalah "C".

Radio vektor

Ini disebut jarak antara titik P dan salah satu lampu sorot.

Jarak fokus

Itu adalah jarak yang memisahkan kedua lampu sorot dan setara dengan 2c.

Sudut

Simpul v₁ dan v₂ Mereka adalah titik di mana hiperbola memotong sumbu asli. Sebuah simpul dan pusat hiperbola dipisahkan dengan jarak A, oleh karena itu, jarak antara simpul adalah 2a.

Sumbu fokus, sumbu utama atau sumbu asli

Itu adalah sumbu di mana lampu sorot berada dan berukuran 2c. Itu dapat ditempatkan di salah satu dari dua sumbu cartesian dan hiperbola memotongnya pada titik yang disebut simpul.

Sumbu transversal, sumbu sekunder atau sumbu imajiner

Itu adalah sumbu tegak lurus terhadap sumbu fokal dan mengukur 2b. Hiperbola tidak memotongnya, jadi itu juga disebut sumbu imajiner.

Asimtot

Mereka adalah dua baris, yang masing -masing tertunda adalah m₁ = (b/a) dan m₂ = - (b/a), yang dimaksudkan di tengah hiperbola. Kurva tidak pernah memotong garis -garis ini dan produk antara jarak mana pun dari hiperbola ke asimtot, itu konstan.

Untuk menemukan persamaan asimtot, cukup cocokkan sisi kiri persamaan kanonik hiperbola dengan 0. Misalnya, untuk hiperbola yang berpusat pada asal:

Persegi panjang hyberbola

Itu adalah persegi panjang yang lebarnya adalah jarak antara simpul 2a dan jarak 2b dan difokuskan pada pusat hiperbola. Konstruksinya memfasilitasi tata letak manual hiperbola.

Sisi lurus

Tali yang melewati salah satu lampu sorot, tegak lurus terhadap sumbu asli.

Keanehan

Itu didefinisikan sebagai hasil bagi antara jarak fokus dan sumbu asli:

E = C/A

Itu selalu lebih besar dari 1, karena C lebih besar dari A, dan kurang dari √2.

Nilai dan menunjukkan apakah hiperbola agak tertutup (persegi panjang sempit, memanjang ke arah sumbu utama) atau terbuka (persegi panjang lebar, memanjang ke arah sumbu imajiner).

Tangen lurus ke hiperbola pada titik P (x₁,Dan₁)

Garis garis singgung ke hiperbola pada titik p (x₁,Dan₁) Ini adalah bisektor dari dua vektor radio pada titik itu.

Untuk hiperbola dengan sumbu utama sejajar dengan sumbu x, kemiringan garis garis singgung ke hiperbola pada titik p (x₁,Dan₁) diberikan oleh:

Dapat melayani Anda: Operasi gabungan

Dan jika hiperbola adalah sumbu utama yang sejajar dengan sumbu y, maka:

Contoh hiperbola

Dispersi partikel alfa oleh nukleus

Dengan membombardir inti atom dengan partikel alfa, yang tidak lain adalah inti helium, ini ditolak, karena inti atom mana pun memiliki muatan positif. Inti helium ini tersebar setelah lintasan hiperbolik.

Lintasan badan tata surya

Gambar 3: Planet Tata Surya

Di tata surya, benda bergerak di bawah aksi gaya gravitasi. Deskripsi gerakan berasal dari persamaan diferensial di mana gaya itu konservatif dan berbanding terbalik dengan kuadrat jarak. Dan solusi dari persamaan ini adalah lintasan yang mungkin terjadi yang mengikuti objek.

Nah, lintasan ini selalu berbentuk kerucut: keliling, elips, perumpamaan atau hiperbolas. Dua yang pertama adalah kurva tertutup, dan ini adalah bagaimana planet bergerak, tetapi beberapa komet masih merupakan lintasan terbuka, seperti perumpamaan atau hiperbola, dengan matahari yang terletak di salah satu lampu sorot.

Suara minimum

Ketika ada dua sumber suara, seperti dua speaker yang memancarkan suara secara merata ke segala arah, yang terletak di sepanjang garis lurus, minimum intensitas suara (gangguan destruktif) berada pada hiperbola yang poros utamanya dikatakan garis, dan dalam lampu sorot Hiperbola adalah speakernya.

Olahraga diselesaikan

Temukan unsur -unsur hiperbola berikut: simpul, fokus, dan asimtot hiperbola dan membangun grafiknya:

Larutan

Pusat hiperbola ini bertepatan dengan asal koordinat dan sumbu aslinya horizontal, karena fraksi positif sesuai dengan variabel x.

Semi -ax hiperbola adalah:

ke² = 16 ⇒ a = 4

B² = 4 ⇒ b = 2

Dengan cara ini, persegi panjang pusat mengukur lebar 4 unit dan 2 unit tinggi. Mengingat bahwa itu disebutkan di atas bahwa c² - ke² = b² , Jadi:

C² = a² + B² ⇒ c² = 16 + 4 = 20

Oleh karena itu, semi-tugas fokal adalah:

C = √20 = 2√5

Dan fokus berada pada titik koordinat f₁ (-2√5.0) dan f₂ (2√5.0).

Lereng asimtot adalah:

m = ± (b/a) = ± (2/4) = ± 0.5

Oleh karena itu persamaan masing -masing adalah:

Dan₁ = 0.5x; Dan₂ = -0.5x

Hiperbola dapat dengan mudah membuat grafik melalui perangkat lunak online seperti Geogebra:

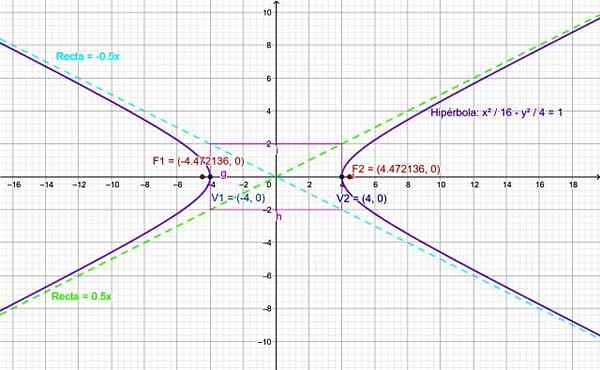Gambar 4. Grafik untuk hiperbola latihan diselesaikan. Sumber: f. Zapata.

Referensi

1. Fisicalab. Persamaan hiperbola. Pulih dari: fisicalab.com
2. Hoffman, J. Pemilihan masalah matematika. Volume 2.
3. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
4. Rumus alam semesta. Hiperbola. Pulih dari: universoformulas.com
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.