Matematika

Homotecia negatif

Homotecia negatif
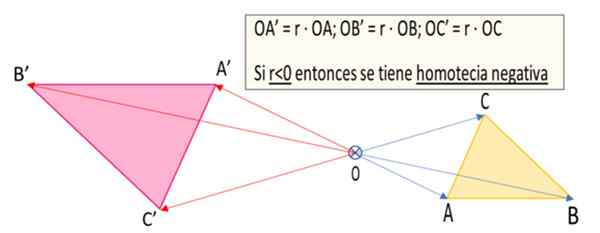
Gambar 1. Segitiga A'B'C 'adalah transformasi homotetik dari segitiga ABC sehubungan dengan titik atau dengan alasan homotecia negatif R = -1.5 (disiapkan oleh: f zapata).

Apa itu homotecia negatif?

Homotecia negatif adalah transformasi di mana poligon yang terkandung dalam bidang memiliki gambarnya poligon lain di bidang yang sama, dengan sudut yang sama dan dengan sisi yang sesuai sebanding dengan yang asli. Saat homotecia negatif gambar diputar setengah belokan sehubungan dengan gambar awal.

Homotecia ditandai dengan memiliki pusat homotecia SALAH SATU dan konstanta proporsionalitas disebut alasan R. Kapan R Ini adalah angka negatif sehingga ada pembicaraan tentang homotecia negatif.

Bagaimana transformasi homotecia dibuat?

Untuk menjelaskan bagaimana homotecia negatif dilakukan, kami akan mengambil kasus Gambar 1 di mana segitiga berada ABC siapa yang ingin membangun homotetik negatifnya.

1.- Itu mulai memilih pusat homotecia, yang merupakan kasus ini adalah intinya SALAH SATU.

2.- Dari SALAH SATU Segmen berorientasi dibangun (vektor) Oa, Ob Dan Oc yang berubah dari pusat homotecia ke masing -masing simpul segitiga.

3.- Alasan homotecia dipilih R. Karena Anda menginginkan homotecia negatif, lalu R Itu pasti kurang dari nol. Dalam kasus Gambar 1 itu diambil R = -1.5.

4.- Vektor ditarik Oa ', Ob ' Dan Oc ', yang masing -masing Oa '= r ∙ oa, Ob '= r ∙ ob  Dan Oc '= r ∙ oc. Sebagai R = -1.5, Itu adalah angka negatif, lalu vektor Oa ', Ob ' Dan Oc ' Mereka memiliki arah yang bertentangan dengan rekan mereka yang sesuai, yaitu Oa, Ob Dan Oc. Tetapi sebagai nilai nalar absolut R adalah | R | = 1.5 ukuran Oa ', Ob' Dan Oc ' Mereka sekali setengah lebih besar dari rekan -rekan mereka Oa, Ob Dan Oc.

5.- Ujung vektor Oa ', Ob ' Dan Oc ' Tentukan simpul segitiga A'b'c ' Apa homotetik negatif dari segitiga ABC.

Sifat homotecia negatif

Itu homotecia negatif, disebut juga Homotecia terbalik, Ini memiliki properti berikut:

Itu dapat melayani Anda: kelipatan 8: apa itu dan penjelasan

1.- Sisi yang sesuai antara poligon gambar dan poligon asli memiliki panjang proporsional, menjadi konstanta proporsionalitas nilai absolut dari rasio homotecia, yaitu gambar tersebut diperkuat dalam suatu faktor | r | selama | r | lebih besar dari unit, tetapi gambar dikurangi jika | r | kurang dari unit.

2.- Sudut antara sisi gambar yang sesuai dan figur asli memiliki ukuran yang sama.

3.- Sisi homolog antara asli dan gambar sejajar satu sama lain.

4.- Segmen yang sesuai dalam kasus homotecia negatif adalah paralel, tetapi dengan panduan atau arah yang berlawanan. Misalnya pada Gambar 1, segmen AB memiliki a'b 'homolog paralel dengan yang pertama, tetapi dengan arah yang berlawanan.

Perbandingan dengan homotecia positif

Ini disebut homotecia positif yang di mana rasio homotecia adalah angka positif. Untuk membangun homotecia positif, langkah yang sama diikuti dengan homotecia negatif:

1.- Pilih pusat homotecia, dalam kasus kami SALAH SATU (Lihat Gambar 2).

2.- Gambar segmen berorientasi (vektor), mulai dari pusat homotecia hingga simpul poligon, dalam kasus Gambar 2 ini adalah: Oa, Ob Dan Oc.

3.- Pilih rasio homotecia yang merupakan angka positif, misalnya, dalam kasus Gambar 2 telah dipilih R = 0.5.

4.- Vektor ditarik Oa ', Ob ' Dan Oc ', yang masing -masing Oa '= r ∙ oa, Ob '= r ∙ ob Dan Oc '= r ∙ oc. Sebagai R Itu adalah angka positif, maka vektor Oa ', Ob ' Dan Oc ' Mereka memiliki alamat yang sama seperti Oa, Ob Dan Oc. Panjangnya Oa ', Ob' Dan Oc ' Mereka setengah dari rekan -rekan mereka Oa, Ob Dan Oc, karena alasannya R = 0.5.

5.- Akhirnya simpul A'B'C 'bergabung untuk mendapatkan segitiga homotetik ke ABC dengan alasan 1/2.

Dapat melayani Anda: segi empat: elemen, properti, klasifikasi, contoh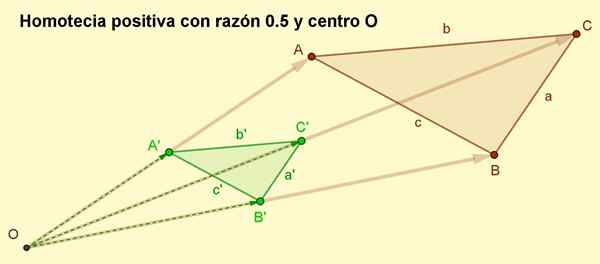 Gambar 2. Homotecia positif dengan benar 0,5 dari hasil segitiga ABC. Dalam homotecia positif orientasi dipertahankan. (Disiapkan oleh: f. Zapata)

Contoh Homotecia

Homotecia muncul dalam berbagai situasi:

Proyektor film

Dalam sebuah proyektor film, gambar yang direkam dalam bingkai diproyeksikan dan diperluas pada layar, dan agar proyeksi terlihat di sebelah kanan perlu bahwa bingkai diinvestasikan, karena pusat homotecia berada di tengah lensa dari Lensa lensa proyektor, antara bingkai dan layar (homotecia negatif, lihat Gambar 3)

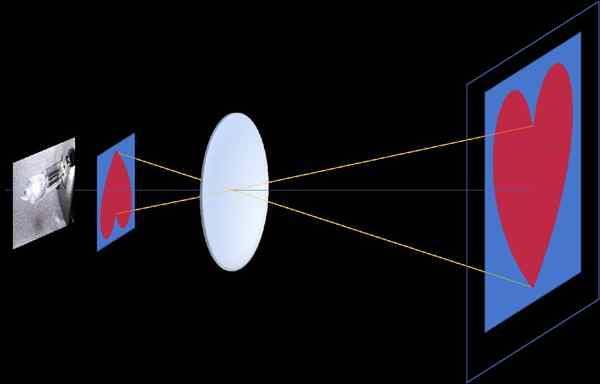Gambar 3. Homotecia negatif muncul dalam proyektor film, antara gambar yang direkam pada bingkai tembus cahaya dan gambar yang diproyeksikan di layar. Pusat Homotecia berada di pusat optik lensa, pada gilirannya terletak di antara bingkai dan layar. Sumber: f. Zapata.

Kamera foto

Prinsip ini juga berlaku untuk kamera: Cahaya dari gambar yang terletak jarak tertentu dari lensa diproyeksikan pada sensor fotografi, yang bisa menjadi film kimia yang sensitif terhadap cahaya atau sensor CCD, jika itu adalah kamera digital.

Gambar yang direkam dalam sensor terbalik sehubungan dengan yang asli dan biasanya secara proporsional kurang dari dia.

Aplikasi praktis

Matahari tidak boleh terlihat secara langsung, karena menyebabkan kerusakan permanen pada retina, tetapi ada dua kemungkinan untuk mempelajarinya: gunakan filter yang melemahkan intensitas cahaya atau memproyeksikan gambarnya di layar.

Dapat melayani Anda: variasi proporsional

Perangkat proyeksi terdiri dari tabung panjang D. Salah satu ujung tabung ditutupi dengan aluminium foil dan bor di tengahnya dengan pin. Ujung lainnya, yang akan berfungsi sebagai layar, ditutupi dengan kertas tembus cahaya, yang dapat berupa kertas bawang atau kertas Albanene (kertas sayuran).

Latihan

Tentukan diameter matahari, mengetahui bahwa jari -jari orbital terestrial adalah urutan 150 juta kilometer, bahwa tabung proyeksi, seperti yang ditunjukkan pada Gambar 4, panjangnya 2,2 meter dan bahwa gambar yang diproyeksikan adalah 2, 1 diameter cm.

Gambar 4. Di dalam tabung untuk memproyeksikan cakram surya rasio homotecia negatif terjadi. Sumber: f. Zapata.

Larutan

Data adalah sebagai berikut:

  • Panjang tabung: D = 2.2m
  • Diameter gambar yang diproyeksikan Sun: S = 2.1 cm
  • Jarak dari tabung matahari: r = 150 x 10^9 m
  • Diameter Matahari Nyata: S = ¿?

Untuk mendapatkan diameter matahari, rasio proporsionalitas diterapkan sesuai dengan proporsionalitas homotecia (lihat Gambar 4):

Jarak ke matahari berada pada panjang tabung karena diameter matahari adalah dengan diameter gambar yang diproyeksikan:

(R / d) = (s / s)

Membersihkan kesetaraan ini bahwa diameter asli matahari memiliki diameter proyeksi dikalikan dengan hasil bagi antara jarak ke matahari dan panjang tabung:

S = S (r / d)

Menempatkan nilai numerik adalah:

S = 2.1 x 10-2 M (150 x 109 m / 2.2 m)

S = 1,43 x 109 M.

Hasil ini ditafsirkan sebagai berikut: Diameter asli matahari adalah 1,43 juta kilometer.

Referensi

  1. Álvaro rendón, ke. R. 2004. Gambar Teknis: Buku catatan aktivitas.
  2. Antonio álvarez de la Rosa, J. L. 2002. Afinitas, homologi dan homotecia.
  3. Baer, ​​r. 2012. Aljabar linier dan geometri proyektif. Couer Corporation.
  4. Hebert, dan. 1980. Matematika Umum, Probabilitas dan Statistik.
  5. Messerve, b. DAN. 2014. Konsep geometri mendasar. Couer Corporation