Interpolasi lagrange

Apa interpolasi Lagrange?

Interpolasi LaGrange adalah metode numerik perkiraan fungsi, yang memanfaatkan polinomial yang melewati titik -titik fungsi tertentu yang diketahui yang dimaksudkan untuk mendekati perkiraan.

Jika fungsi perkiraan lunak, bahkan di luar nilai yang diberikan atau diketahui, polinomial mengambil nilai dekat dengan fungsi yang menarik, terutama jika nilai -nilai ini berada di antara titik yang diberikan. Itulah sebabnya polinomial dianggap sebagai pendekatan yang baik untuk fungsi tersebut.

Gambar 1.- Formula untuk membangun polinomial lagrange. Sumber: f. Zapata.

Sekarang, misalkan Anda ingin memperkirakan suatu fungsi f (x) yang hanya diketahui nilainya X-_yo-, dengan yo dari 0 sampai N-1. Yaitu, mereka saling kenal N poin (X-_yo, Dan_yo) dengan Dan_yo = f (x_yo), Dimana indeks yo Pergi dari 0 sampai N-1.

Dalam metode interpolasi lagrange, polinomial yang mendekati fungsi f (x) Itu adalah polinomial P (x) gelar N-1, dibangun oleh kombinasi linier N Polinomial L_yo(X) gelar N-1. Ini adalah Polinomial lagrange, yang dinyatakan sebagai berikut:

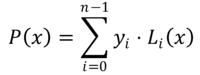
Nilai -nilai Dan_yo Mereka mewakili ordinat yang sesuai dengan absis X_yo Dimana fungsinya f (x) Diketahui, yaitu: Dan_yo = f (x_yo).

Polinomial lagrange

Melalui kombinasi linier di antara mereka, polinomial lagrange bertindak sebagai dasar untuk pembangunan polinomial kelas N -1 yang akan berfungsi untuk interpolasi N poin yang diketahui.

Notasi untuk polinomial adalah l_yo(x), dengan indeks I dalam kisaran dari 0 hingga n-1. Formula untuk membangun polinomial lagrange adalah sebagai berikut:

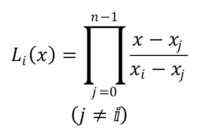
Simbol yang ditunjukkan menunjukkan bahwa produktori monomial n -1 harus dilakukan, mulai dari polinomial j = 0.

Karakteristik polinomial lagrange

1.- Polinomial lagrange persis sama dengan unit ketika dievaluasi di absis yang sesuai dengan indeks mereka, yaitu:

L_yo(X_yo) = 1

2.- Mereka dibatalkan di absis titik interpolasi dengan indeks berbeda dari polinomial yang sama:

Dapat melayani Anda: statistik deskriptif: sejarah, karakteristik, contoh, konsep

L_yo(X_J) = 0, dengan i ≠ j.

3.- Mengambil nilai absis lain yang berbeda dari titik interpolasi, polinomial lagrange memperoleh nilai antara -1 dan +1.

4.- Untuk mendapatkan polinomial lagrange, hanya perlu mengetahui absis titik ke interpoch.

Polinomial Lagrange Kedua

Polinomial Lagrange Kedua adalah yang paling sering digunakan saat Anda ingin melakukan interpolasi tiga poin.

Misalkan fungsi interpolar dikenal dalam tiga titik, yaitu:

(X₀,Dan₀); (X₁, Dan₁); (X₂, Dan₂)

Kemudian polinomial lagrange yang sesuai L₀, L₁ Dan L₂ Mereka menjadi seperti ini:

L₀(x) = [(x - x₁) / (X₀ - X₁)] [(x - x₂) / (X₀ - X₂)]

L₁(x) = [(x - x₀) / (X₁ - X₀)] [(x - x₂) / (X₁ - X₂)]

L₂(x) = [(x - x₀) / (X₂ - X₀)] [(x - x₁) / (X₂ - X₁)]

Perlu dicatat itu L₀(X₀) = L₁(X₁) = L₂(X₂) = 1, ketika L_yo(X_J) = 0 selama yo≠ j.

Polinomial interpolasi dari tingkat kedua

Penting untuk dicatat bahwa dalam polinomial interpolasi Lagrange, ordinat titik interpolasi adalah faktor polinomial Lagrange.

Dengan cara ini, begitu polinomial diperoleh untuk nilai -nilai absis tertentu, mereka berfungsi untuk menghitung polinomial interpolasi dari berbagai fungsi, asalkan yang dipesan dalam absis yang sebelumnya diketahui sebelumnya diketahui diketahui.

Dalam kasus interpolasi kelas dua:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(X)

Dan p (x) mendekati fungsi f (x) dalam interval (X₀, X₂).

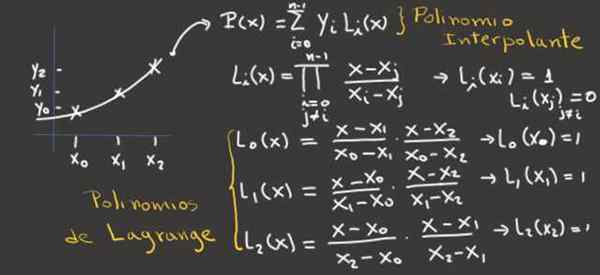Gambar 2.- Gambar ini menunjukkan cara mendapatkan polinomial lagrange untuk tiga titik interpolasi dan dari mereka, polinomial interpoling. Sumber: f. Zapata.

Contoh

Contoh 1

Temukan polinomial lagrange yang sesuai dengan tiga titik absis X₀= 0, X₁= 1 Dan X₂= 2.

Seperti yang terlihat pada bagian sebelumnya, polinomial ini adalah:

Dapat melayani Anda: Fungsi Overjektif: Definisi, Properti, Contoh

L₀(x) = [(x - 1) / (0 - 1)] [(x - 2) / (0 - 2)] = - (x -1) ⋅ (-½) (x - 2) = ½ X² - 3x + 2)

L₁(x) = [(x - 0) / (1 - 0)] [(x - 2) / (1 - 2)] = x ⋅ (-1) (x - 2) = - x² + 2x

L₂(x) = [(x - 0) / (2 - 0)] [(x - 1) / (2 - 1)] = (½) x ⋅ (x - 1) = (½) (x² - X)

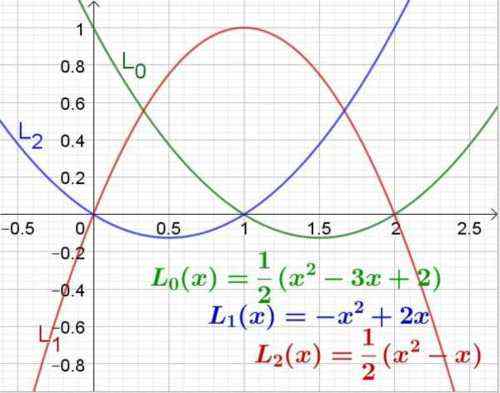Gambar 3. Polinomial Lagrange untuk Nilai Absis 0, 1 dan 2. Sumber: f. Zapata.

Contoh 2

Anda ingin memperkirakan fungsinya f (x) = arcan (x) Dalam interval [0, 2]. Fungsi ini hanya nilainya yang diketahui X₀= 0, X₁= 1 Dan X₂= 2, yang masing -masing Dan₀= 0, Dan₁= π/4 = 0,785 Dan Dan₂= 1.107.

Oleh karena itu Anda harus menemukan polinomial interpoling P (x) mendekat f (x) Dalam interval yang ditunjukkan.

Dalam Contoh 1, polinomial lagrange telah ditentukan untuk nilai absis yang ditunjukkan dalam pernyataan ini, sehingga tidak perlu mengulangi perhitungan. Polinomial interpoling sekarang akan menjadi:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(X)

Yang setara dengan:

P (x) = y₀ L₀(x) + dan₁ L₁(x) + dan₂ L₂(X)

Dalam kasus khusus ini adalah:

P (x) = 0 ∙ (½) (x² - 3x + 2) + 0.785 ∙ (- x² + 2x) + 1.107 ∙ (½) (x² - X)

Di atas disederhanakan untuk:

P (x) = 0,785 ∙ (- x² + 2x) + 1.107 ∙ (½) (x² - X)

Dan akhirnya tetap:

P (x) = -0.2315 ∙ x² + 1.0165 ∙ x

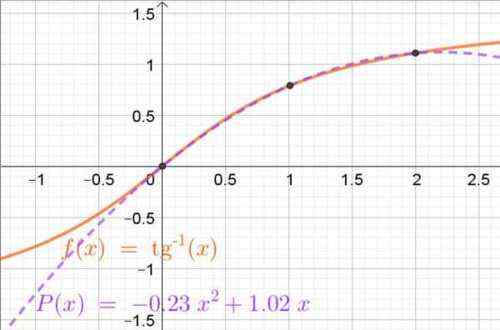Gambar 4. Interpoling polinomial yang diperoleh melalui polinomial lagrange yang mendekati fungsi busur-tangent dalam interval (0, 2). Titik interpolasi juga ditampilkan. Sumber: f. Zapata.

Latihan

Latihan 1

Dapatkan polinomial lagrange yang memadai untuk memiliki pendekatan terhadap fungsi:

f (x) = sin (x)

Dalam interval [0, π] dan dengan lima titik interpolasi.

Larutan

Pertama -tama, absis titik interpolasi ditentukan, yang dipilih sama dan termasuk ujung interval perkiraan. Dengan ini Anda punya:

X₀= 0; X₁= π/4; X₂= π/2; X₃= 3 π/4; X₄= π.

Dapat melayani Anda: Ketimpangan segitiga: demonstrasi, contoh, latihan terpecahkan

Karena f (x) dibatalkan pada titik -titik ekstrem, tidak perlu mendapatkan polinomial lagrange l₀ dan saya₄.

Polinomial l₁, L₂ dan saya₃ adalah:

L₁ = [(x - x₀) / (X₁ - X₀)] [(x - x₂) / (X₁ - X₂)] [(x - x₃) / (X₁ - X₃)] [(x - x₄) / (X₁ - X₄)]

L₂ = [(x - x₀) / (X₂ - X₀)] [(x - x₁) / (X₂ - X₁)] [(x - x₃) / (X₂ - X₃)] [(x - x₄) / (X₂ - X₄)]

L₃ = [(x - x₀) / (X₃ - X₀)] [(x - x₁) / (X₃ - X₁)] [(x - x₂) / (X₃ - X₂)] [(x - x₄) / (X₃ - X₄)]

Sekarang kami mengganti nilai absis:

L₁ = [(x - 0)/(π/4 - 0)] [(x - π/2)/(π/4 - π/2)] [(x - 3 π/4)/(π/4 - 3 π/4)] [(x - π)/(π/4 - π)]

L₂ = [(x - 0)/(π/2 - 0)] [(x - π/4)/(π/2 - π/4)] [(x - 3 π/4)/(π/2 - 3 π/4)] [(x - π)/(π/2 - π)]

L₃ = [(x - 0)/(3 π/4 - 0)] [(x - π/4)/(3 π/4 - π/4)] [(x - π/2)/(3 π/ 4 - π/2)] [(x - π)/(3 π/4 - π)]

Denominator diselesaikan:

L₁ = [x/π/4] [(x - π/2)/( - π/4)] [(x - 3 π/4)/( - π/2)] [(x - π)/( - 3π/4)]

L₂ = [x/π/2] [(x - π/4)/(π/4)] [(x - 3 π/4)/( - π/4)] [(x - π)/( - π /2)]

L₃ = [x/(3 π/4)] [(x - π/4)/(π/2)] [(x - π/2)/(π/4)] [(x - π)/( - π/4)]

Disederhanakan dan dikelompokkan kembali untuk mendapatkan:

L₁ = x (x - π/2) (x - 3 π/4) (x - π)/( - 3 π ⁴/128)

L₂ = x (x - π/4) (x - 3 π/4) (x - π)/(π ⁴/64)

L₃ = x (x - π/4) (x - π/2) (x - π)/( - 3 π ⁴/128)

Latihan 2

Dapatkan polinomial interpolasi yang mendekati fungsi sen (x) dalam interval [0, π] dengan lima titik interpolasi yang dipilih dalam Latihan 1 dan polinomial lagrange masing -masing.

Larutan

Polinomial interpolasi adalah:

P (x) = sin (0) * l₀ + Sen (π/4) * l₁ + Sen (π/2) * l₂ + Sen (3π/4) * l₃ + Sen (π) * l4

Mengevaluasi fungsi sinus dan pengalikan adalah:

P (x) = (√2/2) l₁ + 1 * l₂ + (-√2/2) l₃

Setelah karya aljabar yang sulit, polinomial interpolasi adalah:

P (x) = 2. 7481 x⁴ -limabelas. 138 x³ +23. 467 x² - 9. 5236 x

Referensi

1. Goodman, a. L. H. seribu sembilan ratus sembilan puluh enam. Aljabar dan trigonometri dengan geometri analitik. Pendidikan Pearson.
2. Harpe, hlm. D. (2000). Topik dalam teori kelompok geometris. University of Chicago Press.
3. Hazewinkel, m. (2001). Interpolasi linier ", ensiklopedia matematika.
4. Hoffmann, e. (2002). Hingga kronologi interpolasi: dari astronomi kuno hingga sinyal dan pemrosesan gambar modern. Prosiding IEEE.
5. Wikipedia. Interpolasi polinomial lagrange. Pulih dari: wikipedia.com