Penjelasan terbalik multiplikasi, contoh, latihan diselesaikan
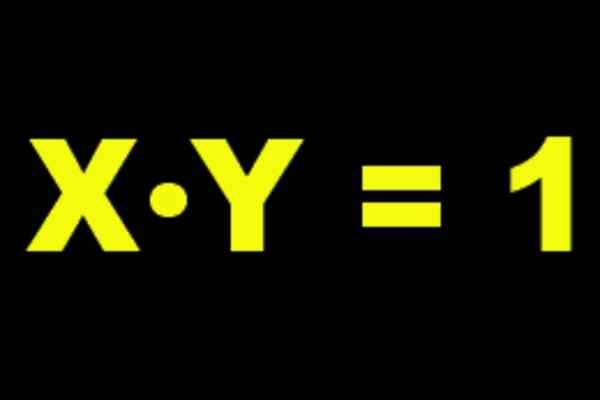
- 1709
- 501
- Pete Lesch
Itu dipahami oleh Inverse Multiplikative Dari satu angka, nomor lain yang dikalikan dengan hasil pertama dalam elemen netral produk, artinya unit. Jika Anda memiliki bilangan real ke Kemudian kebalikan multiplikatifnya dilambangkan dengan ke-1, Dan terpenuhi bahwa:
A A-1 = a-1 A = 1
Biasanya angkanya ke Itu milik set bilangan real.
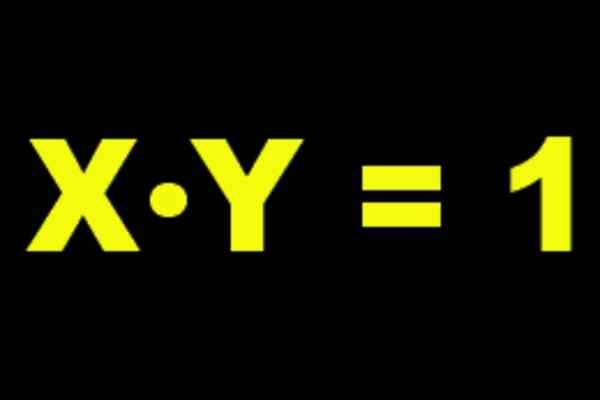 Gambar 1. Dan itu adalah multiplikasi terbalik dari x dan x adalah kebalikan multiplikatif dari y.
Gambar 1. Dan itu adalah multiplikasi terbalik dari x dan x adalah kebalikan multiplikatif dari y. Jika misalnya kita mengambil A = 2, Maka kebalikan multiplikatif Anda adalah 2-1 = ½ karena berikut ini diverifikasi:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2⋅ ½ = ½ ⋅ 2 = 1
Ke Inverse Multiplikative dari sejumlah juga disebut timbal-balik, Karena kebalikan multiplikatif diperoleh dengan menukar pembilang dan penyebut, misalnya kebalikan multiplikasi dari 3/4 adalah 4/3.
Sebagai aturan umum, dapat dikatakan bahwa untuk bilangan rasional (P/Q) Inverse multiplikatif Anda (P/Q)-1 Itu timbal balik (Q/p) Seperti yang dapat diverifikasi di bawah ini:
(p/q) ⋅ (p/q)-1 = (p/q) ⋅ (q/p) = (p⋅ q)/(q⋅ p) = (p⋅ q)/(p⋅ q) = 1
Kebalikan multiplikatif tidak ada di set numerik bilangan bulat, Misalnya, jika seluruh angka 2 diambil, kebalikan multiplikatif sesuai dengan apa yang terlihat di atas adalah ½, tetapi ½ bukan integer.
Ada juga kebalikan multiplikasi dari elemen nol multiplikasi. Dengan kata lain, angka nol (0), yang merupakan elemen nol dari operasi multiplikasi, tidak memiliki kebalikan multiplikasi, karena tidak ada angka yang dikalikan dengan nol unit.
Inverse multiplikasi ada dalam bilangan rasional, dalam bilangan real dan bilangan kompleks.
Contoh terbalik multiplikasi
Contoh 1
Temukan invers 3/2 multiplikatif dan verifikasi bahwa ia memenuhi properti integer multiplikasi.
Dapat melayani Anda: Coplanares Points: Persamaan, Contoh, dan Latihan TerpecahkanMenurut aturan yang diberikan di atas, kebalikan multiplikasi (3/2) adalah (2/3) dipertukarkan dengan cara ini. Untuk memverifikasi perkalian dari dua angka dilakukan:
(3/2) ⋅ (2/3) = (3 ⋅ 2)/(2 ⋅ 3) = 6/6 = 1.
Untuk mengalikan dua angka fraksional, cukup gandakan pembilang yang pertama dengan pembilang kedua untuk mendapatkan pembilang hasil.
Untuk mendapatkan penyebut produk dari angka fraksional, lanjutkan dengan cara yang sama, yaitu, penyebut dikalikan satu sama lain dan hasilnya adalah penyebut produk. Dalam contoh kami, diverifikasi bahwa pembilang produk dari angka dan timbal baliknya adalah 6 dan penyebutnya adalah 6, meninggalkan fraksi 6/6 yaitu 1.
Contoh 2
Kebalikan multiplikatif -5 tidak boleh disamakan dengan simetris (+5) yang kadang -kadang disebut aritmatika terbalik. Kebalikan multiplikatif akan diperoleh sebagai berikut:
(-5) ⋅ x = 1
Di mana x adalah kebalikan multiplikatif yang akan diperoleh. Prosedur yang mungkin terdiri dari membersihkan x yang tidak diketahui. Sebagai (-5) melipatgandakan X yang tidak diketahui di anggota kiri, maka itu terjadi membagi anggota yang tepat:
X = 1 / (-5)
Seperti diketahui + antara - itu - maka akhirnya x diperoleh:
X = - ⅕ .
Kesimpulan - ⅕ adalah kebalikan multiplikatif dari -5.
Contoh 3
Dapatkan kebalikan multiplikatif dari -√2. Misalkan kebalikan multiplikatif adalah x, kemudian -√2 dikalikan dengan x harus berupa unit, suatu kondisi yang kami imposis di bawah ini:
-√2 ⋅ x = 1
Kedua anggota dibagi dengan -√2 untuk mendapatkan:
(-√2 ⋅ x) / (-√2) = 1 / (-√2)
Anggota pertama disederhanakan -"Tersisa:
Itu dapat melayani Anda: kesalahan estimasi standar: bagaimana itu dihitung, contoh, latihanX = 1 / (-√2)
Ekspresi ini dapat dirasionalisasi, yaitu, menghilangkan akar penyebut, berkembang biak dalam pembilang dengan (-√2) dan dalam denominator untuk jumlah yang sama sehingga hasilnya tidak diubah:
X = (-√2) / [(-√2) (-√2)] =-(√2 / 2)
Kesimpulan - (√2/2) adalah kebalikan multiplikatif (-√2).
Contoh 4
Asumsikan angka apa pun x, dapatkan kebalikan multiplikatif Anda dan mewakili secara grafis.
Dalam hal ini adalah fungsi f (x) = x, memperoleh kebalikan multiplikatif adalah untuk menemukan fungsi g (x) yang dikalikan dengan unit pertama unit. Fungsi G adalah fungsi timbal balik dari F dan tidak boleh bingung dengan cara apa pun dengan fungsi terbaliknya.
Dengan kata lain, kebalikan multiplikatif dari x adalah a dan sedemikian rupa sehingga berikut dipenuhi:
x ⋅ y = 1
Di mana harus membersihkan dan memiliki:
y = 1/x.
Di atas ditafsirkan dengan demikian diberi nilai x, rumus sebelumnya memberi kita invers multiplikatifnya.
Dimungkinkan untuk membuat representasi grafisnya seperti yang ditunjukkan pada gambar berikut:
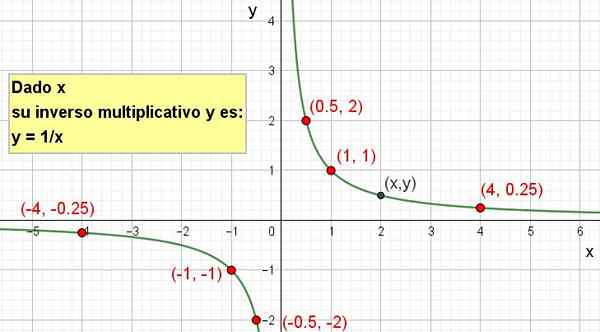 Gambar 2. Kebalikan multiplikatif dari x adalah y = 1/x.
Gambar 2. Kebalikan multiplikatif dari x adalah y = 1/x. Latihan
Latihan 1
Diberikan x = 2 - √2, dapatkan invers multiplikatif Anda dan.
Larutan:
Sehingga dan itu adalah x x multiplikatif
x ⋅ y = 1
X digantikan oleh nilainya:
(2 - √2) ⋅ y = 1
Kemudian jelas dan:
y = 1 / (2 - √2)
Untuk merasionalisasi hasil mengalikan pembilang dan penyebut dengan binomial terkonjugasi:
y = (2 + √2) / ((2 + √2) (2 - √2))
Dalam denominator, produk terkenal diakui disebut produk dari jumlah untuk perbedaan, yang merupakan perbedaan kotak. Dengan cara ini akar menghilang dalam penyebut.
y = (2 + √2) / (2^2 - (√2)^2)
Dapat melayani Anda: proporsiMemecahkan kekuatan:
y = (2 + √2) / (4 - 2)
Menyederhanakan:
y = (2 + √2) / 2
Latihan 2
Dapatkan invers multiplikatif (1/a + 1/b) di mana a dan b berbeda bilangan real.
Larutan:
Kami menelepon dan kebalikan multiplikasi (1/a + 1/b), sehingga persamaan berikut harus dipenuhi:
Dan ⋅ (1/a + 1/b) = 1
Variabel dibersihkan dan:
Y = 1/(1/a + 1/b)
Denominator diselesaikan:
Y = 1 / ((b + a) / a)
Seperti yang diketahui tentang aturan aljabar, penyebut penyebut masuk ke pembilang:
Y = (a b) / (b + a)
Itu diperintahkan untuk akhirnya mendapatkan:
(a b)/(a + b) yang merupakan kebalikan multiplikasi (1/a + 1/b).
Latihan 3
Dapatkan invers multiplikasi (a - b) / (a^2 - b^2).
Larutan:
Ingatlah bahwa kebalikan multiplikatif juga disebut timbal balik karena diperoleh hanya pertukaran pembilang dan penyebut.
Kemudian kebalikan multiplikasi (a - b) / (a^2 - b^2) akan menjadi:
(A^2 - b^2) / (a - b)
Tetapi ungkapan ini dapat disederhanakan jika kita mengenali, sesuai dengan aturan aljabar, bahwa pembilang adalah perbedaan kotak yang dapat memperhitungkan sebagai produk dari jumlah untuk perbedaan:
((A + b) (a - b)) (a - b)
Karena ada faktor umum (A - B) dalam pembilang dan di denominator kami melanjutkan untuk menyederhanakan, akhirnya mendapatkan:
(a + b) yang merupakan invers multiplikasi (a - b) / (a^2 - b^2).
Referensi
- Sumber, a. (2016). Matematika Dasar. Pengantar Perhitungan. Lulu.com.
- Garo, m. (2014). Matematika: Persamaan Kuadrat: Bagaimana Memecahkan Persamaan Kuadratik. Marilù Garo.
- Haeussler, e. F., & Paul, R. S. (2003). Matematika untuk Administrasi dan Ekonomi. Pendidikan Pearson.
- Jiménez, J., Rofríguez, m., & Estrada, R. (2005). Matematika 1 Sep. Ambang.
- Berharga, c. T. (2005). Kursus Matematika 3o. Progreso editorial.
- Rock, n. M. (2006). Aljabar saya mudah! Begitu mudah. Team Rock Press.
- Sullivan, J. (2006). Aljabar dan Trigonometri. Pendidikan Pearson.

