Sisi homolog

Kami menjelaskan apa sisi homolog, dengan contoh dan latihan diselesaikan

Apa sisi homolog?

Itu Sisi homolog Dalam dua figur geometris datar adalah mereka yang saling berhubungan, menjaga kesamaan. Misalnya, tangan kanan seseorang homolog dengan tangan kanan orang lain.

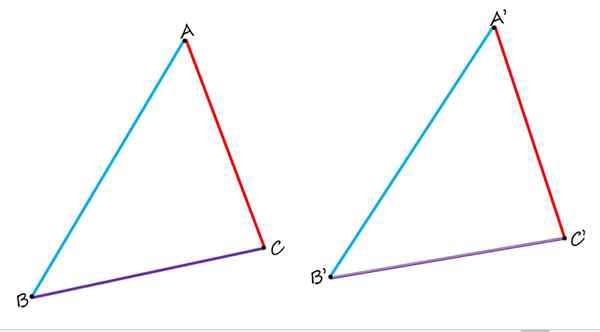
Dalam geometri datar, tidak hanya ada sisi homolog, tetapi juga simpul dan sudut homolog. Untuk melihatnya, pertimbangkan gambar berikut, yang terdiri dari dua segitiga identik ABC dan A'B'C ':

Dalam dua segitiga identik yang ditunjukkan, ab dan a'b ', homolog, serta sisi bc dan b'c' dan ac dan a'c '. Sumber: f. Zapata.

Saat membandingkannya, diamati dengan jelas bahwa sisi AB dan A'B 'berwarna biru, karena mereka menempati posisi yang sama di setiap segitiga. Sisi BC dan B'C 'dalam ungu juga homolog. Dan akhirnya, sisi AC merah homolog ke samping a'c '.

Penjelasan

Dari yang disebutkan di atas, maka sisi homolog adalah posisi yang menempati posisi relatif yang sama dalam gambar dengan cara yang sama. Pada gambar sebelumnya dua segitiga identik digunakan untuk menunjukkan ide, tetapi ini dapat dengan mudah menggeneralisasi figur geometris datar lainnya, yang dibentuk oleh sisi berturut -turut yang dekat.

Angka -angka ini disebut poligon. Misalnya, segitiga dan segi empat adalah poligon masing -masing 3 dan 4 sisi.

Konsep sisi homolog adalah penting karena memungkinkan untuk mendefinisikan kriteria kesamaan antara poligon, seperti yang akan dilihat segera. Angka yang sama memiliki bentuk yang persis sama dan menjaga proporsi yang identik di antara sisi mereka, bahkan jika mereka tidak memiliki ukuran yang sama.

Dan meskipun sejauh ini referensi dibuat hanya untuk angka datar, ada juga angka serupa dalam tiga dimensi. Mereka mudah diamati di rak supermarket, ketika produk yang sama dijual dalam wadah yang identik, tetapi dengan ukuran yang berbeda.

Dapat melayani Anda: logika matematika

Kata -kata lain yang digunakan secara bergantian dalam geometri untuk merujuk pada sisi homolog dalam angka geometris adalah: sisi yang sesuai, sisi masing -masing dan sisi yang setara.

Simpul dan sudut homolog

Seperti halnya sisi, simpul homolog juga didefinisikan, yang menyatukan pasangan sisi homolog. Misalnya, simpul A dan 'dari gambar sebelumnya adalah homolog. Demikian pula, pasangan simpul B dan B 'dan C dan C' adalah homolog.

Akhirnya, sudut homolog menempati posisi relatif yang sama dalam angka. Simpul sudut homolog pada gilirannya homolog.

Untuk mengilustrasikan ide itu, ambil sudut antara sisi biru dan ungu dari segitiga kiri, yang dapat dilambangkan sebagai ∠Abc. Sudut ini memiliki rekannya di sudut ∠a'b'c ', dari segitiga ke kanan.

Titik sudut ini adalah B, yang seperti yang ditunjukkan sebelumnya, adalah rekan dengan B ', dan dua pasang sudut homolog segitiga yang ditampilkan adalah: dua pasang lainnya adalah:

• ∠bca dan ∠b'c'a '
• ∠Cab dan ∠c'a'b '

Kesamaan poligon

Agar dua poligon serupa, kondisi berikut harus dipenuhi:

• Semua pasangan sudut homolog memiliki ukuran yang sama
• Pasangan sisi homolognya sebanding.

Kedua kondisi tersebut harus dipenuhi secara bersamaan untuk memastikan kesamaan. Segera diamati mengapa.

Pada gambar berikut ada dua segi empat yang jelas tidak serupa. Ini karena fakta bahwa status pertama mingguan terpenuhi, tetapi yang kedua tidak:

Dua segi empat yang tidak serupa, meskipun sudut homolog mereka memiliki ukuran yang sama. Sumber: f. Zapata.

Sementara dalam angka -angka pasangan sudut homolog mereka memiliki ukuran yang sama, karena semua sudut lurus (mereka mengukur 90º), angka -angka tidak serupa, karena pasangan sisi mereka tidak proporsional.

Dapat melayani Anda: fungsi suntikan: apa yang terdiri dari, untuk apa dan contohnya

Di sisi lain, dua segi empat ini memiliki sisi homolog dengan ukuran yang sama, tetapi sudut homolog tidak mengukur hal yang sama. Oleh karena itu, angka jelas tidak serupa.

Dua segi empat dengan sisi homolog dengan ukuran yang sama, tetapi dengan sudut internal yang berbeda, oleh karena itu mereka bukan angka yang sama. Sumber: f. Zapata.

Alasan kesamaan

Jika dua angka serupa, hasil bagi di antara sisi homolog adalah sama dan disebut alasan kesamaan.

Menunjukkan sisi salah satu tokoh seperti a, b, c, d ... dan yang sesuai dari sosok lain seperti a ', b', c ', d

Perimeter dan area angka serupa

Rasio kesamaan memungkinkan memperoleh hubungan antara perimeter, area dan volume dari dua angka serupa.

Alasan perimeter untuk dua angka serupa

Perimeter P poligon didefinisikan sebagai jumlah dari semua sisinya. Jika Anda memiliki sosok yang sisinya adalah ', b', c ', d' ..., perimeter p 'adalah:

P '= a' + b ' + c' + d '.. .

Jika poligon lain mirip dengan ini, dan sisinya adalah A, B, C, D ..., dipenuhi bahwa:

Dan maka dari itu:

A = r ∙ a '

Anda dapat menegaskan hal yang sama untuk sisi lain dari gambar ini. Jadi perimeter P dinyatakan sebagai:

P = A + B + C + D .. . = r ∙ a ' + r ∙ b' + r ∙ c ' + r ∙ d' +…

Karena "R" adalah faktor umum bagi semua pecandu, hubungan antara P dan P 'adalah:

P = r ∙ p '

Ini berarti bahwa alasan perimeter antara dua poligon yang sama sama dengan alasan kesamaan.

Alasan untuk area dari dua angka serupa

Jika dua angka serupa masing -masing memiliki area A dan A ', ini terkait melalui:

Dapat melayani Anda: latihan izin formula

A = r²∙ a '

Di mana "r" adalah alasan kesamaan angka.

Rasio volume dua angka serupa

Mereka adalah dua tokoh tiga dimensi yang serupa, yang volume masing -masing, V dan V '. Hubungan di antara mereka, melalui "r" adalah:

V = r³∙ V '

Contoh

Cetak biru

Bagian dari tanah, tanaman bangunan atau bahkan pakaian, dalam skala yang lebih kecil di atas selembar kertas dapat diwakili. Rencana memiliki keuntungan untuk dapat membawa mereka dan membuat modifikasi yang relevan dengan mudah, sebelum dipraktikkan pada objek nyata.

Peta

Mereka biasanya representasi di bidang luas tanah yang luas, dari desa ke benua. Mereka juga dibuat dalam skala tertentu.

Mereka memiliki banyak aplikasi dan ada banyak jenis. Misalnya, melalui peta medan dapat dijelaskan, dan ketika terletak di titik tertentu, rute terbaik untuk pergi dari titik itu ke titik lain ditentukan.

Model

Mereka adalah representasi tiga dimensi pada skala objek seperti mobil, bangunan dan konstruksi secara umum.

Olahraga diselesaikan

Nilai -nilai berikut sesuai dengan sisi beberapa segitiga yang serupa. Temukan alasan kesamaan dan nilai "x" dan "y":

Segitiga 1: 5, 8, 10

Segitiga 2: 150, x, y

Larutan

Alasan kesamaan adalah hasil bagi:

R = 150/5 = 30

Karena itu:

x = 30 × 8 = 240

y = 10 × 30 = 300