Formula dan Persamaan Ampère Hukum, demonstrasi, latihan

Itu Hukum ampère menyatakan bahwa sirkulasi vektor induksi magnetik B Itu sebanding dengan intensitas dan arus yang mengalir dengan hal yang sama.

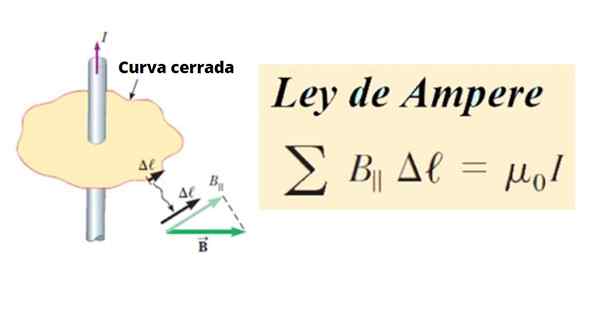
Pada gilirannya sirkulasi B Itu adalah jumlah dari semua produk antara komponen tangensial b_║ dan panjang segmen kecil Δℓ dari kurva tertutup c, Di sekitar sirkuit. Dalam istilah matematika ditulis seperti ini:

∑ b_║ .Δℓ ∝ yo

Gambar 1. Definisi Hukum Ampere. Sumber: Serway, R. Fisika Perguruan Tinggi.

Sebagai garis atau kurva sewenang -wenang, itu dapat dibagi menjadi segmen kecil Δℓ, Dan ini pada gilirannya bisa sangat kecil, maka mereka disebut dℓ.

Dalam hal ini, jumlah menjadi garis integral dari produk skalar antara vektor B dan dS. Produk ini berisi komponen tangensial B, yaitu B Cosθ, di mana θ adalah sudut antara vektor:

Lingkaran kecil yang melintasi integral berarti bahwa integrasi dilakukan pada lintasan tertutup C, yang dalam hal ini melibatkan arus yang mengalir melalui penampang pengemudi.

Konstanta proporsionalitas yang diperlukan untuk menetapkan kesetaraan adalah μ_{salah satu}, Permeabilitas vakum. Dengan cara ini, hukum Ampère tetap:

Hukum Ampère memberi tahu kita bahwa garis integral ∫_C B ∙ dS Itu layak tepat μ_{salah satu}Saya, tetapi tidak menawarkan detail kepada kita tentang bagaimana medan magnet berorientasi B Mengenai kurva C di setiap titik, atau tentang cara menghitung integral. Itu hanya memberi tahu kita bahwa hasil yang sama selalu μ_{salah satu}yo.

[TOC]

Demonstrasi Hukum Ampère

Hukum Ampère diverifikasi secara eksperimental memeriksa medan magnet yang diproduksi oleh konduktor bujursangkar yang sangat panjang. Sebelum mengatasi masalah, dua kasus minat khusus dalam persamaan sebelumnya harus disorot:

Itu dapat melayani Anda: tubuh bercahaya: karakteristik dan bagaimana mereka menghasilkan cahaya sendiri

-Yang pertama adalah kapan B dan dS Mereka paralel, yang berarti itu B adalah tangensial untuk c. Maka sudut antara kedua vektor adalah 0º dan produk skalar hanyalah produk dari magnitudo B.ds.

-Yang kedua terjadi jika B dan dS Mereka tegak lurus, dalam hal ini produk skalar adalah 0, karena sudut antara vektor adalah 90º, yang cosinusnya 0.

Detail penting lainnya adalah pilihan kurva C di mana sirkulasi lapangan dievaluasi. Hukum Ampère tidak menentukan apa yang bisa terjadi, tetapi harus membungkus distribusi saat ini. Juga tidak mengatakan bagaimana melakukan perjalanan kurva dan ada dua kemungkinan untuk ini.

Solusinya adalah menetapkan tanda -tanda sesuai dengan aturan jempol kanan. Keempat jari melengkung ke arah yang ingin Anda integrasikan, biasanya ini akan sama di lapangan B beredar. Jika titik saat ini ke arah ibu jari kanan, sebuah tanda ditugaskan dan jika tidak, tanda tangani -.

Ini berlaku ketika ada distribusi dengan beberapa arus, beberapa bisa positif dan negatif lainnya. Jumlah aljabar dari mereka adalah apa yang akan kita tempatkan dalam hukum ampère, yang biasanya ditunjuk sebagai Arus yang tidak dibatalkan (Untuk kurva c).

Medan magnet kawat bujursangkar dan tak terbatas

Gambar 2 menunjukkan kawat yang mengangkut arus dan keluar dari pesawat. Aturan ibu jari yang benar memastikan itu B Itu beredar ke arah yang berlawanan, menggambarkan keliling seperti yang ditunjukkan panah merah.

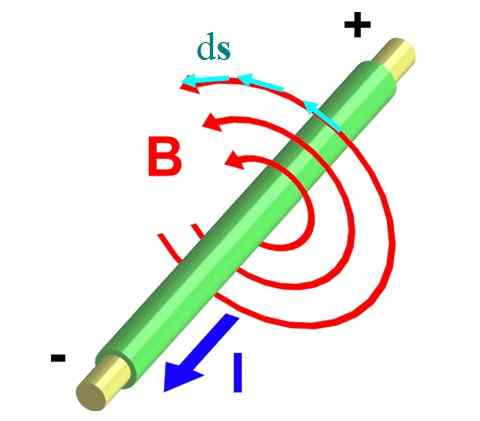Gambar 2.- Medan magnet dari kawat yang tak terbatas. Sumber: Wikimedia Commons.

Mari kita ambil salah satu dari mereka, yang jari -jari itu r. Kami membaginya menjadi segmen diferensial kecil dS, diwakili melalui vektor biru. Kedua vektor, B dan dS, Mereka paralel di setiap titik keliling, dan dengan cara ini integral ∫_C B ∙ dS Itu berubah dalam:

Dapat melayani Anda: arus langsung

∫_C Bds

Ini karena, seperti yang kami katakan sebelumnya, produk skalar B ∙ dS  Ini adalah produk dari magnitudo vektor oleh cosinus 0º. Hasil integral diketahui berkat hukum Ampère, oleh karena itu kami menulis:

∫_C Bds = μ_{salah satu}yo

Karena besarnya bidang konstan di seluruh lintasan, ia meninggalkan integral:

B ∫_C Ds = μ_{salah satu}yo

Integral ∫_C DS mewakili jumlah dari semua segmen yang sangat kecil yang membentuk lingkar radio R, Setara dengan panjangnya, produk jari -jari dengan 2π:

B.2πr = μ_{salah satu}yo

Dan dari sana kami menemukan bahwa besarnya B adalah:

B = μ_{salah satu}I / 2πr

Perlu untuk menekankan bahwa bahkan jika lintasan yang dipilih (atau Sirkuit Amperian) Tidak melingkar, hasil integral terus menjadi μ_{salah satu}I, bagaimanapun ∫_C B ∙ dS Itu tidak lagi b.2πr.

Itulah sebabnya kegunaan hukum Ampère untuk menentukan medan magnet terletak pada memilih distribusi dengan simetri tinggi, sehingga integral mudah dievaluasi. Lintasan melingkar dan bujursangkar memenuhi persyaratan ini.

Latihan terpecahkan

- Latihan 1

Pertimbangkan kurva A, B, C dan D yang ditunjukkan pada Gambar 3. Mereka membungkus tiga arus, dua yang meninggalkan pesawat, dilambangkan dengan satu titik ( . ), yang intensitasnya adalah 1 A dan 5 A, dan arus yang memasuki bidang, yang dilambangkan dengan salib dan yang besarnya 2 a.

Temukan arus yang terlampir oleh setiap kurva.

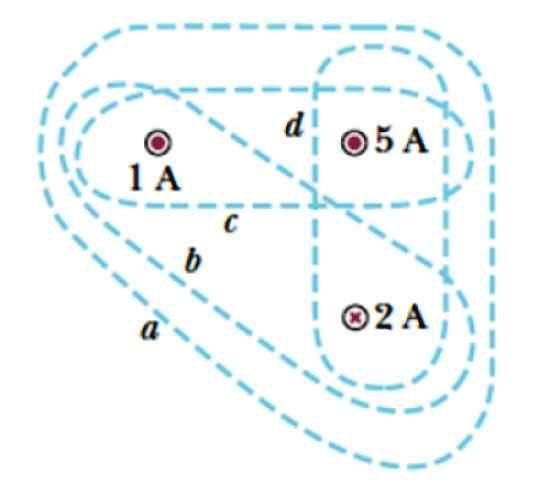Gambar 3. Beberapa kurva untuk menerapkan hukum Ampère. Sumber: Serway, R. Fisika Perguruan Tinggi.

Larutan

Arus yang meninggalkan kertas diberi tanda +. Menurut Ini:

Itu dapat melayani Anda: Gelombang dangkal: Karakteristik, jenis dan contoh

Kurva a

Melampirkan tiga arus, oleh karena itu arus tertutup adalah + 1 a + 5 a - 2 a = 4 a.

Kurva b

Hanya arus 1 a y - 2 a di dalam kurva ini, oleh karena itu arus terlampir dari - 2 a.

Kurva c

Berisi arus keluar 1 dan 5 a, oleh karena itu arus tertutup adalah 6 a.

Kurva d

Arus di dalamnya adalah +5 A dan - 2 A, kemudian melampirkan arus bersih 3 ke.

- Latihan 2

Hitung besarnya medan magnet yang dihasilkan oleh kawat bujursangkar yang sangat panjang.

Larutan

Menurut hukum Ampère, bidang kawat diberikan oleh:

B = μ_{salah satu}I / 2πr = (4π x 10^-7 x 1/2π x 1) t = 2 x 10^-7 T.

Referensi

1. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 6. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
2. Knight, r.  2017. Fisika untuk Ilmuwan dan Teknik: Pendekatan Strategi.  Pearson.
3. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 2.
4. Serway, r. 2009. Fisika Perguruan Tinggi. Pembelajaran Cengage.
5. Tipler, hlm. (2006) Fisika untuk Sains dan Teknologi. Edisi ke -5. Volume 2. Editorial dikembalikan.