Hukum Fick

Apa itu Hukum Fick?

Itu Hukum Fick Ini adalah persamaan matematika yang menghubungkan aliran massa yang disebarluaskan dalam media dengan konsentrasi atau gradien tekanan. Itu diformulasikan pada tahun 1855 oleh ahli fisiologi Jerman dan dokter Adolf Fick, yang terinspirasi oleh hukum Fourier (konduksi termal) dan Ohm (konduksi listrik), memodelkan proses difusi oksigen ke alveoli paru -paru paru -paru.

Hukum Fick menyajikan kekhasan bahwa itu tidak hanya berlaku untuk fenomena difusi kimia atau biokimia, tetapi juga pada apa pun jenis alam. Oleh karena itu, ia berfungsi untuk memodelkan penyebaran atom antara padatan, menjadi sangat berguna dalam fisika bahan dan rekayasa.

Representasi proses difusi melalui membran semipermeabel. Sumber: Gabriel Bolívar.

Namun, basis pusat adalah sama untuk hampir semua fenomena difusi, yang diilustrasikan di atas. Partikel ungu, menjadi atom atau molekul, disebarkan melalui membran tebal semipermeabel dan area transversal ke. Di sebelah kiri kami memiliki konsentrasi yang lebih besar C₁ partikel yang di sebelah kanan, c₂.

Hukum Fick menetapkan yang berikut: Aliran massa yang disebarluaskan melalui permukaan sebanding dengan gradien konsentrasi (c₂-C₁/L) dan konstanta D yang disebut difusi atau koefisien difusivitas.

Undang -undang ini memiliki dua bentuk: satu berdasarkan ruang (x), dan yang lain tergantung pada ruang dan waktu (x, t). Yang pertama berlaku untuk sistem dalam kondisi stasioner, sedangkan yang kedua untuk sistem nyata, non -stasioner.

Hukum Pertama Fick

Komponen dan persamaan

L tebal membran semipermeabel mewakili jarak (x) yang harus ditempuh partikel untuk mencapai sisi lain. Seperti yang dapat dilihat pada gambar, partikel ungu semakin banyak mereka menjauh dari kompartemen kiri, di mana c₁ Itu bagus, konsentrasinya berkurang ke nilai c₂. Artinya, konsentrasi berubah sepanjang ketebalan membran, yang bergantung pada x.

Variasi konsentrasi ini tergantung pada jarak adalah apa yang dikenal sebagai gradien konsentrasi: (c₂-C₁)/L o (c₂-C₁)/X. Perhatikan bahwa nilainya negatif (-1), karena c₂ > C₁.

Di sisi lain, kami juga memiliki kecepatan partikel yang tersebar melalui membran atau ruang yang dimaksud. Kecepatan ini tergantung pada ukuran dan massa partikel, serta sifat lingkungan dan suhu. Koefisien difusi D mewakili kecepatan ini, dan dapat konstan atau tidak selama difusi.

Dapat melayani Anda: filter laboratorium): Karakteristik, fungsi, jenis

Dan akhirnya, kami memiliki aliran massa 'J' yang melintasi area melintang membran atau saluran tempat partikel menyebar. Mengelompokkan istilah -istilah ini, persamaan Hukum Pertama Fick lahir:

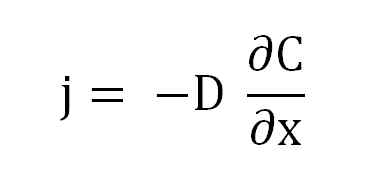Persamaan Hukum Pertama Fick. Sumber: Gabriel Bolívar.

Di mana j proporsional dengan d dan a (∂c/∂x), gradien konsentrasi.

Interpretasi dan unit

Simbol negatif dalam persamaan berfungsi untuk menetralkan tanda negatif dari gradien konsentrasi. Kalau tidak, J akan memiliki nilai negatif, yang tidak dilapisi. Demikian juga, nilai D adalah positif, sehingga dengan mengalikan dengan tanda negatif yang mendahului, memberikan nilai negatif.

Hukum pertama Fick menunjukkan yang berikut: Semakin besar gradien konsentrasi (∂c/∂x), semakin besar aliran massa j. Yaitu perbedaan antara c₂ dan C₁ Itu menjadi lebih besar dan, oleh karena itu, lebih banyak partikel akan menyebar melalui membran.

Di sisi lain, J juga tergantung pada D, yang pada gilirannya tergantung pada parameter seperti suhu, viskositas, berat molekul, dan area melintang untuk:

D ∝ (a/l) (s/√m_W)

Di mana s adalah kelarutan partikel yang tersebar dengan lingkungan, dan m_W Berat molekulnya.

Mengenai unit komponen atau ketentuan persamaan yang kami miliki:

-C (kg · m^-3 atau mol · m^-3)

-D (m^-2· S^-1)

-J (kg · m^-2· S^-1 atau mol · m^-2· S^-1)

Perpindahan kuadrat medium net

Selama diseminasi, partikel bertabrakan satu sama lain, dan setelah interval waktu yang singkat berakhir dengan menempuh jarak yang sangat besar Δx. Namun, tergantung pada arti perpindahan ini, Δx dapat memiliki nilai negatif atau positif (sesuai dengan titik asal). Itulah sebabnya rata -rata nilai Δx untuk semua molekul cenderung 0.

Di sisi lain, nilai Δx sangat kecil dibandingkan dengan jarak yang menjalankan partikel. Ketika mereka bertabrakan, mereka kehilangan mobilitas ke arah suatu arah, akibatnya memiliki perpindahan bersih yang terbatas; Misalnya, kemajuan 2 cm dalam satu arah setelah bepergian ratusan meter dalam tabrakan dan rebound.

Einstein pada tahun 1905 menemukan ekspresi matematika untuk gulungan rata -rata perpindahan (karena itu berbeda dari 0):

<(Δx)²> = 2dt

Mendefinisikan

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

(Δx)_Rms Ini adalah perpindahan kuadratik rata -rata dari partikel yang dimaksud. (Δx)_Rms Ini memberi tahu kita berapa banyak partikel bergerak rata -rata (dalam arah positif atau negatif) sesuai waktu. Beberapa partikel akan bergerak lebih jauh atau terdekat dari (Δx)_Rms, menyebabkan distribusi Gaussian.

Dapat melayani Anda: kalsium oksida (CAO)

Hukum Kedua Fick

Persamaan

Hukum pertama Fick menggambarkan difusi dalam kondisi stasioner, yaitu, aliran massa J tidak bervariasi dari waktu ke waktu. Namun, dalam sistem nyata, kami memiliki kondisi non -stasiun, di mana aliran massa tidak hanya bervariasi dalam ruang, tetapi juga dari waktu ke waktu. Oleh karena itu, ia tertarik untuk menentukan (∂c/∂t).

Di bawah ini kami memiliki dua persamaan yang mewakili hukum kedua Fick:

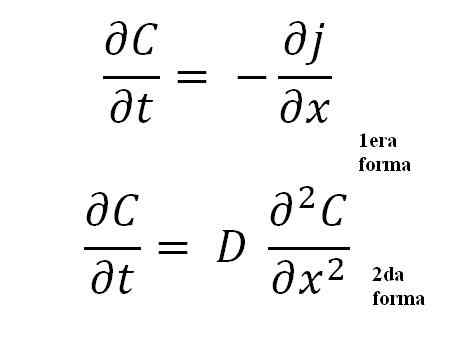Persamaan Hukum Kedua Fick. Sumber: Gabriel Bolívar.

Bentuk ke -2 adalah yang paling penting dari semua, karena mewakili persamaan matematika umum untuk setiap proses penyebaran; Baik termal, listrik, atom, dll.

Deduksi

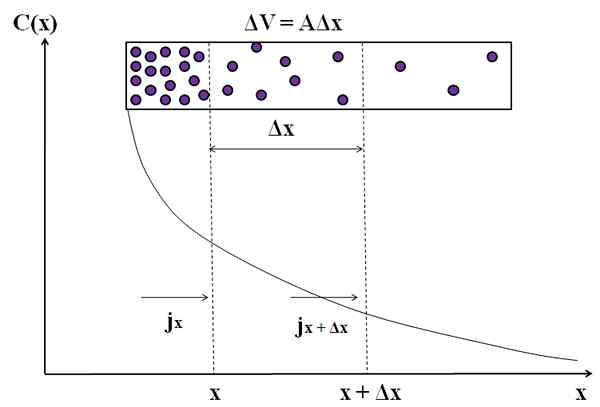Representasi grafis tentang bagaimana aliran massa tidak konstan dalam penyebaran molekul -molekul ini. Sumber: Gabriel Bolívar.

Pertimbangkan lagi partikel ungu di ruang persegi panjang. Di antara jarak x dan x+Δx kami memiliki aliran j_X (masuk) dan j_x+Δx (keluar). Volume kamera antara jarak ini ditentukan oleh:

ΔV = AΔX

Perhatikan bahwa grafik C (x) vs x tidak berasal dari garis lurus, jadi kami memiliki nilai yang berbeda dari j (j_X ≠ j_x+Δx). Kita harus menentukan Δc/Δt.

Massa m_X Itu akan sama dengan:

M_X = J_X AΔT

Analisis dimensi membantu memahami mengapa:

kg = (kg · m^-2· S^-1) (M²) (S)

Dengan cara yang sama kami menghitung m_x+Δx:

M_{x+ Δx} = J_x+Δx AΔT

Menjadi massa yang menumpuk di wilayah itu sama dengan ΔM:

ΔM = m_X - M_{x+ Δx}

= (j_X - J_{x+ Δx}) AΔt

= -(j_{x+ Δx} - J_X) AΔt

= -ΔJaΔt

Dan mengetahui bahwa ΔC = ΔM/ΔV

ΔC = -ΔJAΔT/ ΔV

= -ΔJaΔt /aΔx

= -ΔjΔt/Δx

Kami menghapus ΔC/Δt

Δc/Δt = -Δj/Δx

Ekspresi ini menunjukkan bahwa variasi konsentrasi dari waktu ke waktu sama dengan variasi aliran J sehubungan dengan perpindahannya. Menerapkan batas untuk Δt dan Δx yang cenderung ke 0 kita mendapatkan ekspresi yang sama dengan turunan parsial:

∂c/∂t = -(∂j/∂x) (bentuk 1)

Akhirnya, formulir ke -2 diperoleh dengan mengganti J dengan hukum pertama Fick:

∂c/∂t = -∂/∂x (-d∂c/∂x)

= D (∂²C/∂x²) (Formulir ke -2)

Latihan terpecahkan

Dalam latihan berikut, sistem yang sangat sederhana akan dipertimbangkan yang tidak diketahui yang dapat diselesaikan menggunakan hukum pertama Fick.

Latihan 1

Penyataan

Dalam pipa panjang 15 meter dan lebar 21 sentimeter, dan yang juga jenuh dengan nitrogen, arus oksigen tersebar dari satu ujung ke ujung lain pada suhu 0 ºC. Mengetahui bahwa tekanan di sisi kiri (p₁) adalah 20 kg/m³, Dan tekanan di sisi kanan (p₂) adalah 10 kg, tentukan:

Itu bisa melayani Anda: ion hidronio

a) Aliran massa yang tersebar

b) berapa kilogram atau₂ Mereka akan menyebar melalui pipa dalam 17 menit?

c) gradien konsentrasi atau tekanan

d) Tekanan O₂ pada jarak 7 meter dari pintu masuk ke pipa

e) Berapa 80 kg o₂ dalam menyebar melalui pipa ini?

Pertimbangkan itu d_O2-N2 sama dengan 1.8 · 10^-5 M²· S^-1.

Resolusi

Dari hukum pertama Fick, kita harus menyelesaikan ayat a):

J = -d (p₂-P₁)/L

= -(1.8 · 10^-5 M²· S^-1) (10-20) (kg/m³)/(15 m)

= 1.2 · 10^-5 kg · m^-2· S^-1

Untuk b) kita membutuhkan area pipa:

A = π (0.21 m)²

= 0.14 m²

Dan kami melipatgandakan J dengan A dan waktu t untuk menentukan massa atau₂ Tidak adil:

M_O2 = (1.2 · 10^-5 kg · m^-2· S^-1) (17 s) (0.14 m²)

= 3.57 · 10^-5 kg

Sekarang, untuk ayat c) kami memiliki gradien sama dengan:

Gradien = (p₂-P₁)/L

= (10-20) (kg/m³)/15 m

= -2/3 (kg/m³) · M^-1

Tapi kami mengambil nilai positif, yang masuk akal secara fisik:

2/3 (kg/m³) · M^-1

Nilai ini kemudian akan melayani kita untuk menyelesaikan ayat d) Jika gradien ditafsirkan dengan baik: setiap meter tekanan atau₂ 2/3 kg/m akan jatuh³. Dengan menyebarkan 7 meter yang akan kita miliki:

2/3 (kg/m³) · M^-1 (7 m) = 14/3 atau 4.7 kg/m³

Artinya, tekanan pada jarak itu adalah:

(20-4.7) (kg/m³) = 15.3 kg/m³

Dan akhirnya, ayat e) mirip dengan b), hanya saja kita sekarang jelas waktu dan bukan massa:

M_O2 = Jat

t = m_O2/Ja

= (80 kg)/(1.2 · 10^-5 kg · m^-2· S^-1) (0.14 m²)

= 47619.04 s atau 0.55 hari

Latihan 2

Penyataan

Tentukan (Δx)_Rms Untuk sukrosa dalam air pada t = 1 menit, 1 jam dan 1 hari. Koefisien diseminasi sukrosa dalam air adalah 0.52 · 10^-5cm²· S^-1.

Resolusi

Kami menerapkan persamaan:

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

Kami mengevaluasi (Δx)_Rms Dengan waktu yang diungkapkan dalam hitungan detik. Untuk t = 1 menit atau 60 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (60an))^1/2

= 0.025 cm

Untuk t = 1 jam atau 3600 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (3600 -an))^1/2

= 0.19 cm

Dan akhirnya untuk t = 1 hari atau 86400 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (86400))^1/2

= 0.95 cm

Perhatikan bahwa seiring berjalannya waktu molekul sukrosa bahkan belum dapat bergerak 1 cm ke arah apa pun.

Referensi

1. Walter J. Moore. (1963). Kimia Fisik. Dalam Kinetika Kimia. Edisi Keempat, Longmans.
2. Iran. Levine. (2009). Prinsip -prinsip fisikokimia. Edisi Keenam. MC Graw Hill.
3. Pengantar Ilmu dan Teknik Bahan. (11 Maret 2018). Hukum Kedua Fick. Prof. Rajesh Prasad. [Video]. Dipulihkan dari: YouTube.com
4. Wikipedia. (2020). Hukum Difusi Fick. Diperoleh dari: di.Wikipedia.org
5. Laura Dickson. (10 September 2020). DIFUSI. Libretteks Kimia. Pulih dari: chem.Librettexts.org
6. Larissa Zhou et al. (1 September 2015). Memahami teori difusi dan hukum Fick melalui makanan dan memasak. Masyarakat Fisiologis Amerika. doi.org/10.1152/Advan.00133.2014