Formula Hukum Hooke, contoh, aplikasi, latihan

Itu Hukum Hooke menunjukkan bahwa deformasi yang dialami oleh objek elastis berbanding lurus dengan gaya yang diterapkan di atasnya. Konstanta proporsionalitas tergantung pada sifat objek, geometri dan materi yang diproduksi.

Semua bahan memiliki sifat elastis pada tingkat yang lebih besar atau lebih kecil, sehingga mereka mematuhi hukum Hooke setiap kali mereka kembali ke dimensi aslinya, begitu gaya berhenti. Pegas elastis dan gusi adalah contoh yang baik dari benda -benda yang mematuhi hukum Hooke, tetapi begitu juga cabilla baja yang merupakan bagian dari jembatan.

Gambar 1. Hukum Hooke di Musim Semi

Mengambil contoh pegas atau dermaga, agar tetap diregangkan atau dikompres, perlu untuk menerapkan gaya yang besarnya f. Menurut Hukum Hooke, musim semi akan mengalami deformasi X:

F ∝ x

Konstanta proporsionalitas, yang, menjadi pegas, disebut kekakuan musim semi, Itu dilambangkan sebagai k, oleh karena itu: oleh karena itu:

F = k⋅x

Dalam unit sistem internasional, pasukan datang di Newton (N) dan deformasi dalam meter (m). Oleh karena itu, konstanta pegas memiliki unit N/M. Konstanta pegas mewakili gaya yang harus diterapkan untuk merusaknya dalam 1 m panjangnya.

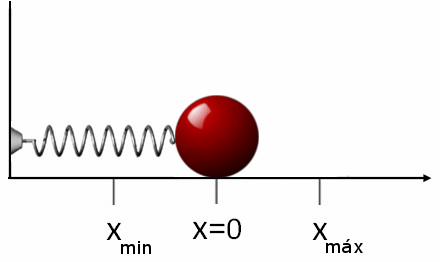Gambar 2. Saat pegas diregangkan, gaya yang diberikan pada objek bertentangan. Hal yang sama terjadi jika pegas menyusut, dalam hal ini ia mendorong objek dalam arti yang berlawanan. Sumber: Wikimedia Commons.

Jika setelah meregangkan atau mengompresi pegas dilepaskan, ia akan bergerak ke arah yang berlawanan dengan gaya yang diterapkan. Ini berarti bahwa jika kita meregangkannya, itu dikompresi dan sebaliknya. Itulah sebabnya Force f_R itu Latihan Musim Semi adalah:

F_R = -k⋅x

Tanda negatif menunjukkan apa yang dikatakan: bahwa kekuatan menentang perpindahan, jadi gaya ini dikenal sebagai Kekuatan restoratif.

[TOC]

Formula dan Persamaan

Hubungan antara kekuatan dan perpindahan di musim semi ditemukan oleh Robert Hooke (1635-1703), seorang ahli fisika Inggris yang terkenal dan dikenal karena persaingannya dengan Isaac Newton. Hooke adalah seorang ilmuwan serba guna yang berhasil berkecimpung di bidang sains yang berbeda: mekanika, biologi, astronomi dan arsitektur.

Gambar 3. Fisikawan Inggris Robert Hooke, yang tidak tahu potret saat itu. Ini adalah rekonstruksi yang dibuat oleh seniman Rita Gerer pada tahun 2004 melalui deskripsi yang ditinggalkan oleh mereka yang bertemu dengan ilmuwan. Sumber: Wikimedia Commons. Rita Greer / Fal.

Hooke menyadari bahwa jika gaya yang diterapkan pada dermaga tidak terlalu besar, dermaga secara proporsional berubah bentuk untuk memaksa, dan begitu gaya mengatakan menghilang, pegas memiliki panjang alami lagi.

Dapat melayani Anda: magnetosfer bumi: karakteristik, struktur, gas

Dengan cara ini, hukum Hooke secara grafis memiliki bentuk garis lurus, yang kemiringannya adalah konstanta pegas. Gambar berikut menunjukkan gaya yang diberikan pada pegas untuk meregangkannya - atau mengompresnya - tergantung pada posisi x. Perhatikan bahwa gaya tidak tergantung pada panjang alami pegas, tetapi pada perpindahannya.

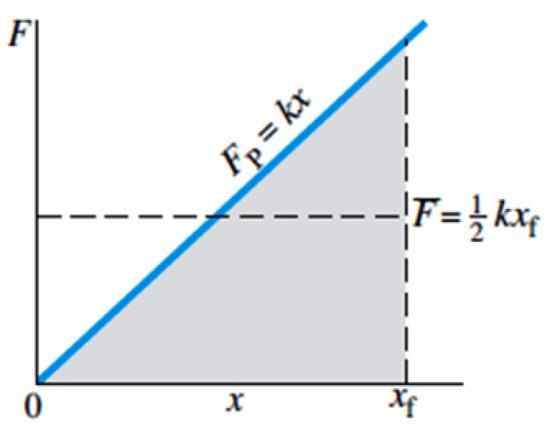Gambar 4. Besarnya gaya yang diperlukan untuk meregangkan atau mengompres pegas, tergantung pada deformasi x. Sumber: Giancoli, D. Fisika dengan aplikasi.

Gaya rata -rata ditunjukkan dalam grafik oleh F dengan batang dan setara dengan ½ kx_F, dimana x_F adalah posisi terakhir musim semi.

Baik gaya yang diberikan pada pegas, dan kekuatan yang ia berikan pada objek yang terkait dengannya, adalah gaya variabel. Semakin banyak Anda ingin meregangkan atau mengompres ke pegas, semakin banyak kekuatan yang harus Anda terapkan untuk dapat mencapainya.

Pekerjaan dilakukan untuk meregangkan atau mengompres pegas

Saat gaya diterapkan yang merusak musim semi, sebuah karya yang disimpan di musim semi dilakukan dan yang dapat digunakan nanti.

Pekerjaan mekanis didefinisikan sebagai area di bawah grafik gaya F tergantung pada posisi x. Untuk menghitung pekerjaan W yang dibuat oleh gaya variabel F (x) saat memindahkan objek dari posisi x₁ untuk memposisikan x₂ Integral yang ditentukan harus dihitung:

Dalam hal pekerjaan yang diperlukan untuk membawa pegas dari posisi keseimbangannya untuk memposisikan x_F Ini sangat sederhana, karena area yang akan dihitung adalah segitiga berbayang abu -abu dari Gambar 4, yang rumusnya diketahui:

Area segitiga = ½ dasar. tinggi

Oleh karena itu pekerjaan yang diperlukan adalah:

W = ½ x_F . (KX_F) = ½ k (x_F)²

Dan jika Anda ingin menghitung pekerjaan yang diperlukan untuk dibawa ke pegas dari posisi x ke posisi x_F, Akan setara dengan menghitung luas trapeze yang tergores pada Gambar 5:

W = ½ k (x_F)² - ½ k x²

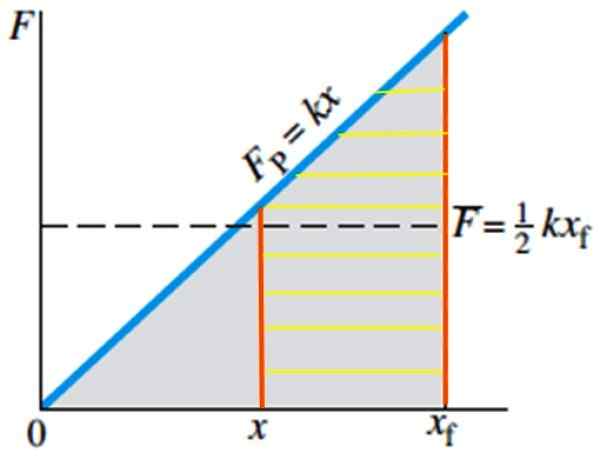Gambar 5. Pekerjaan yang dilakukan untuk meregangkan pegas dari posisi X ke posisi XF yang setara dengan area Rayada. Sumber: Giancoli, D. Fisika dengan aplikasi.

Contoh Mata Air

Menurut aplikasi yang dimaksudkan, pegas dapat berupa silinder, kerucut, spiral, dengan penampang melingkar (bagian yang paling umum), dari bagian persegi atau persegi panjang.

Dapat melayani Anda: konduktor listrik

Klasifikasi yang banyak digunakan sesuai dengan jenis upaya yang akan mereka sasaran: ada torsi, fleksi, kompresi dan pegas ekstensi. Yang terakhir digunakan secara luas dan ada juga bekerja untuk ketegangan dan kompresi.

Pegas kompresi

Contoh pegas kompresi adalah apa yang digunakan dalam mainan yang disebut Pogo salah satu Saltoín Palo. Mata air ini menyimpan energi yang cukup potensial saat dikompresi dan dilepaskan secara bertahap saat kembali ke posisi ekuilibrium. Dengan cara ini rebound tidak terlalu tiba -tiba.

Gambar 6. Pogo atau tongkat saltoín didasarkan pada pegas kompresi. Sumber: Wikimedia Commons.

Perpanjangan dan Torsion Springs

Pegas untuk spramps adalah jenis pegas ekstensi dan diproduksi dengan belokan yang baik, dengan dua kait di ujungnya. Mereka dapat mempertahankan energi potensial yang cukup, yang kemudian mereka lepaskan ketika seseorang bangkit dan mulai melompat di atas kanvas, yang juga memiliki respons elastis mereka sendiri, seperti semua bahan.

Pegas torsi sangat umum, karena mereka berfungsi untuk membuat klem pakaian. Alih -alih kait di ujungnya, mereka menekuk pada sudut, untuk menahan kekuatan yang cenderung melakukan torsion.

Gambar 7. Mata air adalah bagian dari mekanisme yang tak terhitung banyaknya, seperti pinset pakaian ini. Sumber: PXFUEL.

Bahan untuk manufaktur mata air

Bahan yang paling cocok untuk membuat mata air adalah yang memiliki a Perlawanan tertinggi (Perlawanan akhir), yaitu, mereka mendukung upaya besar sebelum melanggar. Juga nyaman bahwa bahan tersebut memiliki titik creep tinggi, sehingga tidak kehilangan kualitas elastisnya dengan upaya kecil.

Mata air penggunaan industri diproduksi dengan paduan yang mencakup baja dengan kandungan karbon tinggi, tembaga, nikel dan perunggu.

Aplikasi Hukum Hooke

Karena pegas memiliki keutamaan menyimpan energi potensial ketika mereka meregangkan atau mengompres, mereka dapat melakukan pekerjaan dengan memindahkan hal -hal seperti mekanisme.

Dengan cara ini mata air memiliki banyak aplikasi, dari benda kecil dan harian, melalui mobil, hingga mesin dari semua jenis. Mata air berfungsi untuk:

-Getaran kejutan.

-Mekanisme yang dapat ditarik: pena, pinset gantung, kait rambut.

-Membuat musim semi atau dinamometer

Dan mereka juga merupakan bagian dari mekanisme:

Dapat melayani Anda: sirkuit listrik tertutup

-Jam tangan.

-Trampolin.

-Kunci.

-Mainan.

-Senjata.

-Meter jarum, misalnya galvanometer, digunakan untuk mengukur arus, tegangan dan resistensi.

Latihan terpecahkan

- Latihan 1

Kekuatan magnitudo 5 diterapkan.0 n di pegas, membuat 3 peregangan panjang.5 cm dari panjang alaminya.

a) berapa banyak yang diregangkan saat gaya yang diterapkan adalah 7 n?

b) Temukan pekerjaan yang dilakukan oleh gaya yang diterapkan untuk meregangkan ke pegas 3.5 cm dari panjang alaminya.

Solusi untuk

Mengetahui bahwa pegas itu peregangan 3.5 cm melalui aplikasi 5.0 n Kami dapat menghitung konstanta Anda:

k = f / x = 5.0 n / 3.5 cm = 1.43 n / cm.

Ketika gaya 7 N diterapkan, peregangan berikut diperoleh:

x = f / k = 7.0 n / 1.43 n/m = 4.9 cm

Solusi b

Pekerjaan yang diperlukan untuk merusak pegas diberikan oleh:

W = ½ kx² = 0.5 x 1.43 n / cm x (3.5 cm)² = 8.76 n . CM = 8.76 n . 1 x10 ^-2 m = 0.0876 J.

- Latihan 2

Segera adonan tercela dan panjang 10 cm menggantung dari dukungan. Jika massa 2 kg digantung, musim semi diregangkan sampai mencapai 15 cm. Menghitung:

a) konstanta musim semi

b) Ukuran pegas saat massa 3 kg ditangguhkan.

Solusi untuk

Peregangan musim semi adalah x = 15 - 10 cm = 5 cm

Karena sistem berada dalam keseimbangan statis, gaya yang diberikan oleh pegas ketika peregangan diarahkan secara vertikal ke atas, untuk mengkompensasi berat, yang diarahkan ke bawah, kemudian:

F_R = W → kx = mg

K = 2 x 9.8 n / 5 x10 ^-2 M = 392 n/m

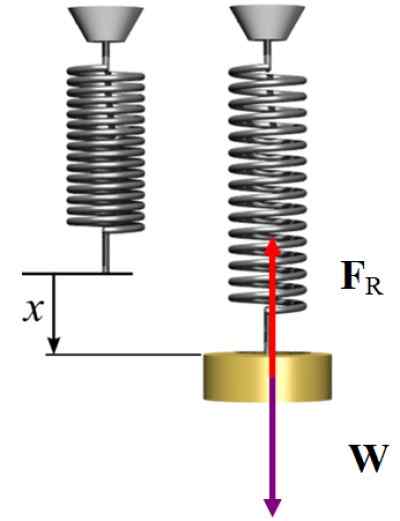Diagram Tubuh Gratis Untuk Latihan Diselesaikan 2. Sumber: Wikimedia Commons/F. Zapata.

Solusi b

Ketika berat 3 kg ditangguhkan, gaya baru adalah W = 3 x 9.8 n = 29.4 n

Dalam hal ini, peregangannya adalah:

x = mg /k = 29. 4 n / 392 n / m = 0.075 m = 7.5 cm

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
2. Blog Mekanisme Kreatif. Empat jenis mata air yang berbeda. Pulih dari: mekanisme kreativem.com.
3. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 2. Dinamis. Diedit oleh Douglas Figueroa (USB).
4. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6. Ed. Prentice Hall.
5. Knight, r.  2017. Fisika untuk Ilmuwan dan Teknik: Pendekatan Strategi.  Pearson.