De Morgan Laws

Kami menjelaskan apa hukum Morgan, kami menunjukkannya dan memberi contoh

Gambar 1.- Matematikawan Augustus dari Morgan (1806-1871) dan hukumnya tentang logika proposisional. Sumber: f. Zapata.

Apa Hukum De Morgan?

Hukum De Morgan adalah dua undang-undang logis yang termasuk dalam logika proposisional yang dirumuskan oleh matematika bahasa Inggris Augustus dari Morgan (1806-1871). Mereka menetapkan yang berikut, sehubungan dengan proposisi logis majemuk:

1. Kebalikan dari konjungsi adalah setara dengan disjungsi yang dibentuk dengan lawan atau penolakan proposal yang membentuk konjungsi.
2. Penolakan disjungsi dapat dinyatakan sebagai konjungsi yang terdiri dari lawan atau penolakan proposisi yang terlibat dalam disjungsi.

Dalam notasi logika proposisional, hukum de Morgan dinyatakan dengan cara yang kompak dan lebih formal seperti ini:

1. ∼ (p ∧ q) ⇔ ∼p ∨q
2. ∼ (p ∨ q) ⇔ ∼p ∧q

Apa yang diungkapkan oleh undang -undang ini adalah bahwa, baik dalam penolakan konjungsi atau disjungsi, hasilnya setara dengan menolak masing -masing proposisi yang berpartisipasi secara terpisah dan menginvestasikan konektor yang menghubungkannya.

Untuk pemahaman yang lebih baik tentang hukum de Morgan, perlu untuk meninjau makna proposisi dan simbol yang digunakan dalam logika proposisional, untuk melihat bagaimana undang -undang ini berlaku dengan mudah.

Notasi logis

Alat dasar logika proposisional adalah proposisi. Proposisi logis adalah pernyataan yang mengakui a nilai sesungguhnya, Apakah itu benar atau salah, tetapi tidak keduanya pada saat bersamaan. Dalam hal ini tidak ada ambiguitas yang diizinkan, yaitu, tidak ada keraguan.

Proposisi dilambangkan dengan huruf kecil, seperti dalam contoh -contoh berikut:

• T: Mexico City adalah ibukota Meksiko (benar).
• T: Dengan menambahkan 2 dan 3, 4 (salah) diperoleh.
• A: Semua mamalia adalah hewan darat (salah).

Dapat melayani Anda: heptagon

Ada juga proposisi yang lebih kompleks, yang disusun melalui penggunaan proposisi sederhana, seperti ini:

• T: Carlos akan pergi ke bioskop jika tidak hujan.
• T: Ana adalah ahli kimia atau ahli biologi kelautan.
• A: Juan akan makan malam atau Pedro akan melihat permainan di televisi.

Konektor logis

Konektor logis adalah simbol yang digunakan untuk menghubungkan proposisi sederhana dan dengan demikian membangun proposisi yang lebih kompleks. Dalam logika proposisional masing -masing memiliki makna tertentu.

Konektor yang paling banyak digunakan adalah konjungsi, disjungsi, disjungsi eksklusif, penolakan, persyaratan dan bi-conditionity.

Konjungsi

Konjungsi dilambangkan dengan huruf "V" terbalik. Proposisi gabungan melalui konjungsi dilambangkan p ∧ Q, sebagai berikut:

• P ∧ T: Mexico City adalah ibu kota Meksiko dan berada di Amerika Utara.

Mudah untuk mengidentifikasi di sini bahwa P adalah "Mexico City adalah ibu kota Meksiko" dan Q adalah "di Amerika Utara".

Pemisahan

Dua jenis disjungsi dibedakan: yang lemah dan eksklusif. A disjungsi yang lemah Itu dilambangkan dengan ∨ dan dalam notasi logis itu adalah p ∨ q. Contoh disjungsi semacam ini adalah:

• P ∨ T: Juan adalah pemain sepak bola atau Juan adalah pemain tenis.

Sebagai gantinya, disjungsi eksklusif Ini dilambangkan dengan tanda ⊻ dan menyiratkan bahwa salah satu proposisi harus dikesampingkan, misalnya:

P ⊻ T: Alicia berusia 20 tahun atau Alicia berusia 22 tahun.

Perbedaan antara kedua jenis itu jelas, dalam disjungsi eksklusif, salah satu proposisi dikesampingkan, karena jika Alicia berusia 20 tahun, ia tidak bisa berusia 22 dan sebaliknya. Di sisi lain, dalam disjungsi yang lemah, Juan mungkin pemain sepak bola dan pemain tenis pada saat yang sama.

Penyangkalan

Dengan menempatkan simbol ∼ proposisi, ini ditolak, seperti dalam:

• T: ∼ (Veracruz adalah ibukota Meksiko).

Yang dibaca sebagai "Veracruz bukanlah ibu kota Meksiko". Cara lain untuk mengekspresikan penolakan, selain dari "tidak", adalah melalui frasa seperti "adalah salah", "itu adalah kebohongan bahwa" dan "tidak benar bahwa".

Dapat melayani Anda: interpolasi linier

Persyaratan

Mereka adalah proposisi gabungan yang biasanya menggunakan kata -kata "ya" dan "lalu ..." untuk menghubungkan dua proposisi di mana ada persyaratan atau implikasi. Bagian dari proposisi yang ditulis segera setelah "ya" adalah mendahului melambai hipotesa dari proposisi dan apa yang setelah istilah "kemudian" adalah kesimpulan salah satu akibat.

Simbol yang digunakan untuk persyaratan adalah panah dari kiri ke kanan "→", oleh karena itu persyaratan antara dua proposisi direpresentasikan sebagai p → Q, yang dapat dibaca sebagai "jika p, maka q". Misalnya:

P → T: Jika hujan pada sore hari maka saya tidak akan bermain tenis.

Bi-conditionality

Dalam jenis proposisi ini frasa "ya, dan hanya jika" untuk menghubungkan dua proposisi, yang disebut anggota bikondisi pertama dan kedua digunakan. Simbol yang digunakan adalah panah dua arah "↔".

Dua proposisi yang terhubung melalui "Ya, dan hanya jika" disebut masing -masing Pertama Dan anggota kedua dan bi-conditionality dari dua proposisi P dan Q tetap sebagai P ↔ Q. Misalnya:

P ↔ T: Maria suka mengendarai sepeda jika dan hanya jika hari itu cerah.

Demonstrasi Hukum De Morgan

Hukum De Morgan adalah bagian dari kesetaraan logis dan dapat ditunjukkan melalui tabel kebenaran, yang digunakan untuk mengetahui nilai kebenaran (benar atau salah) dari suatu proposisi.

Karena konjungsi hanya benar ketika p dan q benar, tabel kebenarannya adalah:

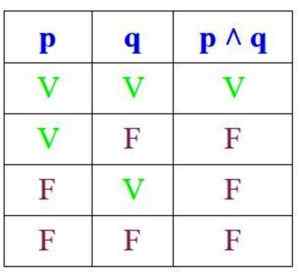
Di sisi lain, dalam disjungsi, proposisi itu benar jika p dan q benar atau jika setidaknya satu dari mereka, tetapi itu salah jika keduanya adalah:

Dapat melayani Anda: permutasi tanpa pengulangan: rumus, demonstrasi, latihan, contoh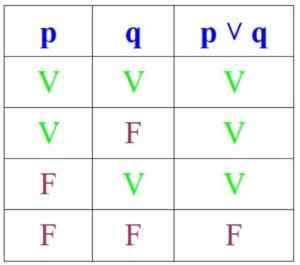

Sekarang, penolakan mengubah kebenaran menjadi salah dan sebaliknya. Dalam hal ini, nilai -nilai kebenaran ∼ (p ∧ Q) dan ∼ (p ∨ q) adalah kebalikan dari nilai -nilai kebenaran (p ∧ Q) dan (p ∨ Q):

Dan harus diverifikasi bahwa hasil ini diperoleh saat melaksanakan tabel kebenaran masing -masing (∼ p ˅ ∼ q) dan (∼ p ˄ ∼ q):

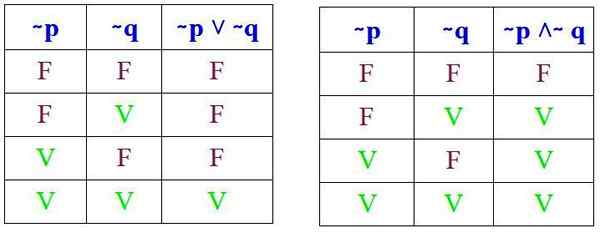
Dan memang, ketika membandingkan tabel kebenaran masing -masing, diamati bahwa hukum de Morgan terpenuhi. Sekarang dua contoh aplikasinya akan terlihat.

Contoh 1

Terapkan undang -undang de Morgan untuk menemukan ekspresi yang setara dari: ∼ (∼p ˅ ∼q)

• Larutan

Ekspresi yang diberikan dibandingkan ∼ (∼p ˅ ∼q) dengan hukum Morgan:

∼ (p ∨ q) ⇔ ∼p ∧q

Dan diamati bahwa penolakan sudah di luar tanda kurung dalam kedua kasus, oleh karena itu instruksi hukum diikuti: ia menolak ∼p, menolak ∼Q dan konektor diubah:

∼ (∼p ˅ ∼q) ⇔ ∼ (∼p) ∧ ∼ (∼q) ⇔ p ∧ q

Contoh 2

Tentukan ekspresi setara ∼ [∼p ˄ ∼ (∼q)] ≡

• Larutan

Pertama, penolakan ∼Q disederhanakan:

∼ [∼p ˄ ∼ (∼q)] ⇔ ∼ [∼p ˄ Q]

Karena sudah ada penolakan di luar braket, ekspresi yang dihasilkan dibandingkan dengan hukum Morgan: ∼ (p ∧ q) ⇔ ∼p ∨q

Untuk menyelesaikan ∼ [∼p ˄ Q] Anda harus menyangkal ∼p, menyangkal Q dan mengubah konektor:

∼ [∼p ˄ Q] ⇔ (∼p) ∨ ∼q ⇔ p ˅ ∼q

Referensi

1. Becerra, J.M.  Catatan Logika UNAM.
2. Cemerlang. Dari Hukum Morgan. Pulih dari: brilian.org.
3. Tutorial Elektronik. Oleh teorema Morgan. Pulih dari: elektronik-tormales.WS.
4. López, f. Pengantar logika matematika. Dipulihkan dari: YouTube.com
5. Muñoz, c. Pengantar logika. Diperoleh dari: situs web.UCM.adalah.