Hukum Kirchhoff

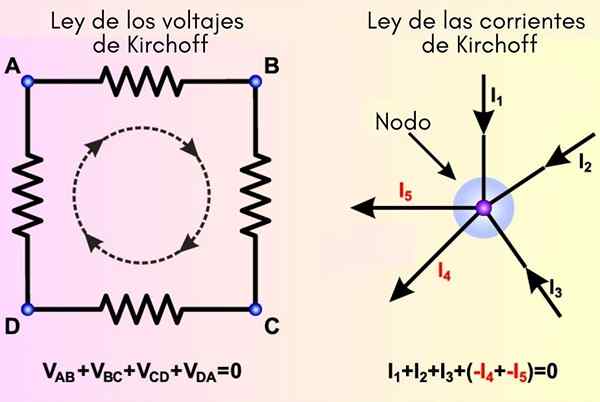
Hukum Kirchoff berasal dari prinsip -prinsip energi dan konservasi beban, masing -masing. Di sebelah kiri, hukum jerat ditetapkan dan di sebelah kanan arus

Apa hukum Kirchoff?

Itu Hukum Kirchoff Mereka terdiri dari menerapkan prinsip konservasi muatan listrik dan prinsip konservasi energi ke sirkuit listrik, untuk menyelesaikan mereka yang memiliki beberapa jerat.

Aturan-aturan ini, karena mereka bukan undang-undang dalam arti yang ketat, disebabkan oleh fisikawan Jerman Gustav Kirchoff (1824-1887). Penggunaannya sangat penting ketika hukum OHM tidak cukup untuk menentukan tegangan dan arus di sirkuit.

Sebelum pernyataan dan penerapan hukum Kirchoff, lebih mudah untuk mengingat arti beberapa konsep penting tentang sirkuit listrik:

• Node: Titik serikat antara dua atau lebih kabel konduktif.
• Cabang: Elemen sirkuit yang berada di antara dua node berturut -turut, yang melaluinya arus yang sama bersirkulasi.
• Mesh: lintasan lintasan atau tertutup yang terdiri dari dua cabang atau lebih dan itu ditempuh ke arah yang sama, tanpa melalui titik yang sama.

Hukum pertama Kirchoff

Ia juga dikenal sebagai hukum arus atau aturan node, dan menetapkan itu:

Jumlah arus yang memasuki node sama dengan jumlah arus yang keluar darinya.

Jadi, dengan cara matematis, hukum pertama dinyatakan sebagai:

∑ i = 0

Dimana simbol σ menunjukkan jumlah.

Persamaan sebelumnya menetapkan bahwa, karena muatan listrik tidak dibuat atau dihancurkan, seluruh arus (beban per unit waktu) yang memasuki simpul harus sama dengan yang keluar darinya.

Dapat melayani Anda: satelit buatan

Contoh

Untuk dengan mudah menerapkan hukum arus, sebuah tanda ditugaskan ke arus yang masuk, dan tanda yang berlawanan dengan arus yang keluar. Pilihannya benar -benar sewenang -wenang.

Gambar berikut ini menunjukkan dua arus yang memasukkan node, digambar dengan warna merah: i₁ dan saya₂, dan ketika meninggalkan mereka ditampilkan dengan warna hijau: arus i₃, yo₄ dan saya₅.

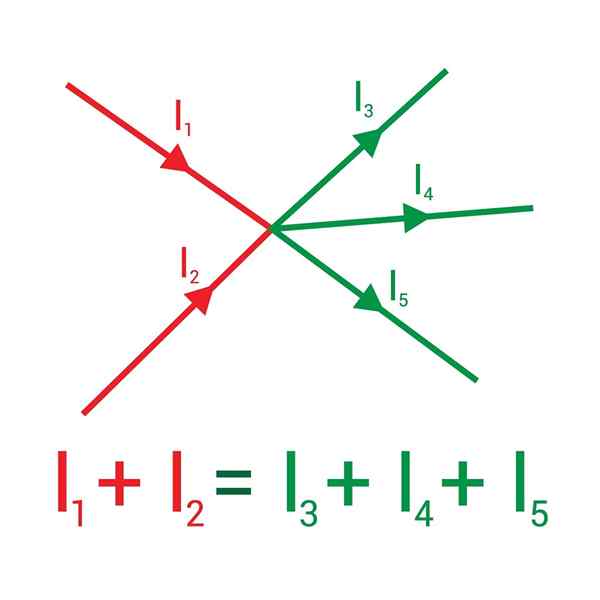Jumlah arus yang masuk ke simpul sama dengan jumlah arus yang keluar darinya

Menetapkan tanda (+) ke arus yang masuk, dan (-) untuk keluar, aturan pertama Kirchoff menetapkan bahwa:

yo₁ + yo₂ - yo₃ - yo₄ - yo₅= 0 ⇒ i₁ + yo₂ = I₃ + yo₄ + yo₅

Hukum Kedua Kirchoff

Nama lain untuk hukum kedua Kirchoff adalah: Hukum Tegangan, Hukum ketegangan salah satu Hukum mesh. Bagaimanapun, ia menetapkan itu:

Jumlah tegangan aljabar turun sepanjang mesh sama dengan 0.

Ini adalah cara untuk menerapkan konservasi energi di sirkuit, karena tegangan di setiap elemen adalah perubahan energi per unit beban.

Oleh karena itu, saat bepergian bagian tertutup (mesh), jumlah aljabar dari tegangan meningkat dan jatuh adalah 0 dan dapat ditulis:

∑ V = 0

Contoh

Pada gambar berikut Anda memiliki mesh Abcda, di mana arus beredar ke arah jarum jam dan rute dapat dimulai pada titik mana pun di sirkuit.

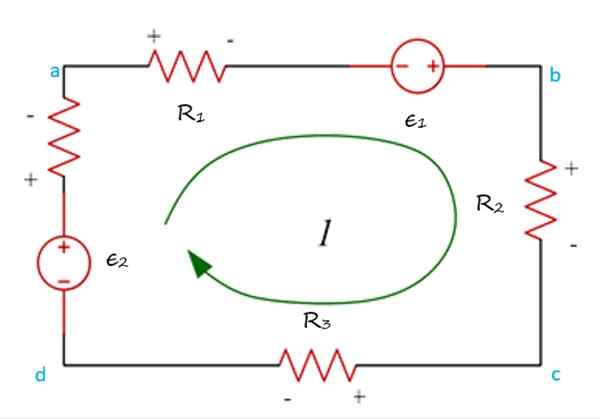Contoh mesh yang di -tur dalam jadwal, di mana peningkatan dan potensi jatuh ditunjukkan untuk menerapkan undang -undang ketegangan Kirchoff. Sumber: f. Zapata.

Itu juga perlu. Biasa adalah menetapkan sebagai positif kenaikan tegangan, yaitu, ketika arus beredar dari ( -) ke (+). Kemudian, penurunan tegangan, yang terjadi ketika arus berubah dari (+) ke ( -), negatif.

Dapat melayani Anda: silikon oksida (SiO2): struktur, sifat, penggunaan, mendapatkan

Memulai rute mesh di titik "A", adalah resistensi R₁. Di dalamnya, beban mengalami penurunan potensial, dilambangkan dengan tanda -tanda (+) di sebelah kiri dan ( -) di atas resistensi.

Oleh karena itu, tegangan atau tegangan di R₁ Itu memiliki tanda negatif.

Kemudian Anda mencapai sumber tegangan langsung, yang disebut ε₁, yang polaritasnya kurang (-) Lebih banyak (+). Di sana muatan listrik mengalami peningkatan potensial dan sumber ini dianggap positif.

Mengikuti prosedur ini untuk resistensi yang tersisa dan sumber lainnya, persamaan berikut ini diperoleh sebagai hasilnya:

−v₁ + ε₁ - V₂ - V₃ + ε₂ = 0

Dimana v₁, V₂ dan v₃ adalah ketegangan dalam resistensi r₁, R₂ dan r₃. Ketegangan ini dapat ditemukan dari hukum Ohm: v = i · r.

Olahraga diselesaikan

Temukan nilai arus i₁, yo₂ dan saya₃ ditunjukkan pada gambar.

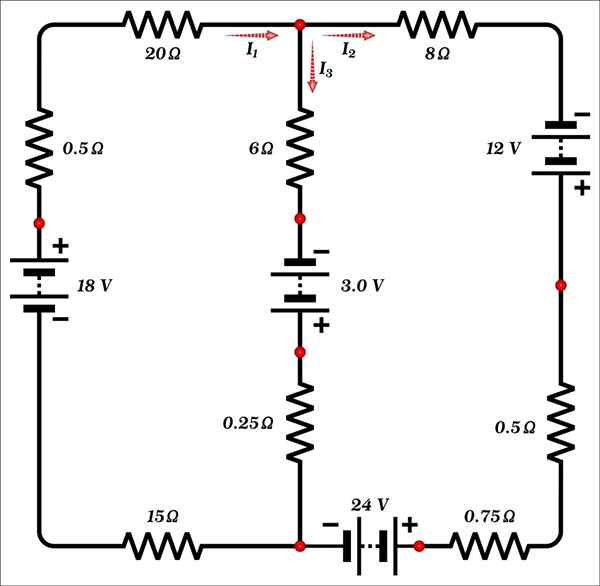
Larutan

Sirkuit ini hanya terdiri dari dua jerat dan memiliki 3 tidak diketahui: arus dan₁, yo₂ dan saya₃, Jadi setidaknya 3 persamaan diperlukan untuk menemukan solusinya.

Di simpul (titik ditandai dengan warna merah) yang berada di bagian atas sirkuit di cabang tengah, diamati bahwa saat ini i₁ masuk, sementara arus saya₂ dan saya₃ Mereka ramah.

Oleh karena itu, undang -undang arus Kirchoff mengarah ke persamaan pertama:

1) i₁ - Saya₂ - Saya₃ = 0

Node yang lebih rendah memberikan informasi yang sama, oleh karena itu, langkah selanjutnya adalah melakukan perjalanan jerat.

Mesh pertama

Untuk menetapkan persamaan berikut, mesh di sebelah kiri dilalui dalam jadwal, mulai dari sudut kiri atas. Ini adalah pengertian di mana arus dan arus beredar₁ dan saya₃.

Dapat melayani Anda: pembanding optik: untuk apa dan bagiannya

Perhatikan bahwa:

• yo₁ melewati resistansi 20 Ω, 15 Ω dan 0.5 Ω dan baterai 18 V, di mana ia mengalami potensi kenaikan.
• Untuk bagiannya, saya₃ Itu melintasi resistensi cabang pusat 6 Ω dan 0.15 Ω dan pada 3 baterai.0 V adalah potensi kenaikan.

Demikian juga, hukum ohm v = i ∙ r digunakan untuk menetapkan ketegangan di setiap perlawanan, menurut ini:

−20 ∙ i₁ - 6 ∙ i₃ + 3.0 - 0.25 ∙ i₃ −15 ∙ i₁ + 18.0 - 0.5 ∙ i₁ = 0

Memesan persyaratan:

(−20 −15 - 0.5) ∙ i₁ - (6 + 0.25) ∙ i₃  = - 3.0 - 18.0

−35.5 ∙ i₁ - 6.25 ∙ i₃ = - 21.0

2) 5 ∙ i₁ + 6.25 ∙ i₃ = 21.0

Mesh kedua

Persamaan ketiga diperoleh dengan berkeliling mesh di sebelah kanan, mulai dari simpul bagian atas sirkuit. Diamati bahwa:

• yo₂ Pergi melalui resistensi 8 Ω, 0.5 Ω dan 0.75 Ω, ditambah baterai 12 V dan 24 V. Menurut polaritas baterai, dalam rute ada peningkatan potensi dalam 12 V dan penurunan 24 V.
• Penting: Tur mesh kedua (dalam jadwal) bertentangan dengan i₃, Oleh karena itu, tegangan dalam resistansi 6 Ω dan 0.25 Ω adalah kenaikan potensial dan membawa tanda positif. Menurut polaritas baterai, ada kenaikan 12 V dan jatuh pada 24 V dan 3 V.

Dengan semua ini yang Anda jangkau:

−8 ∙ i₂ - 0.5 ∙ i₂ - 0.75 ∙ i₂ + 12.0 - 24.0 + 0.25 ∙ i₃ - 3.0 + 6 ∙ i₃ = 0

3) −25 ∙ i₂ + 6.25 ∙ i₃ = 15.0

Perhitungan saat ini

Persamaan 1), 2) dan 3) membentuk sistem 3 persamaan linier dengan 3 tidak diketahui, yang solusinya adalah:

yo₁ = 0.381 a; yo₂ = -0.814 a; yo₃ = 1.195 a

Tanda negatif dalam arus saya₂ berarti mengalir ke arah yang berlawanan dari skema.