Aljabar vektor

Apa aljabar vektor?

Dia Aljabar vektor Ini adalah cabang matematika yang bertugas mempelajari sistem persamaan linier, vektor, matriks, ruang vektor dan transformasi liniernya. Ini terkait dengan bidang -bidang seperti teknik, resolusi persamaan diferensial, analisis fungsional, penelitian operasi, grafik komputasi, antara lain.

Lain dari area yang diadopsi aljabar linier adalah fisika, karena melalui ini dimungkinkan untuk mengembangkan studi fenomena fisik, menggambarkannya melalui penggunaan vektor. Ini memungkinkan pemahaman yang lebih baik tentang alam semesta.

Fundamental

Aljabar vektor berasal dari studi Kuarter (perpanjangan bilangan real) 1, i, j, dan k, serta geometri Cartesian yang dipromosikan oleh Gibbs dan Heaviside, yang menyadari bahwa vektor akan berfungsi sebagai instrumen untuk mewakili beberapa fenomena fisik.

Aljabar vektor dipelajari melalui tiga fondasi:

Secara geometris

Vektor diwakili oleh garis yang memiliki orientasi, dan operasi seperti jumlah, pengurangan dan perkalian dengan bilangan real didefinisikan melalui metode geometris.

Secara analitis

Deskripsi vektor dan operasinya dilakukan dengan angka, yang disebut komponen. Jenis deskripsi ini adalah hasil dari representasi geometris karena sistem koordinat digunakan.

Secara aksiomatis

Deskripsi vektor dibuat, terlepas dari sistem koordinat atau segala jenis representasi geometris.

Studi tentang angka -angka dalam ruang dilakukan melalui representasinya dalam sistem referensi, yang dapat dalam satu atau lebih dimensi. Di antara sistem utamanya adalah:

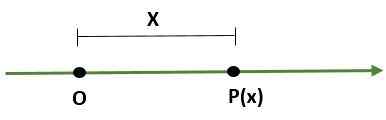
• Sistem unidimensional, Bahwa itu adalah garis di mana titik (atau) mewakili asal dan titik lain (p) menentukan skala (panjang) dan arah ini:

• Sistem koordinat persegi panjang (dua -dimensi), yang terdiri dari dua garis tegak lurus yang disebut sumbu x dan y, yang melewati titik (atau) asal; Dengan cara ini rencana dibagi menjadi empat wilayah yang disebut kuadran. Dalam hal ini, titik (p) dalam bidang diberikan oleh jarak yang ada antara sumbu dan p.

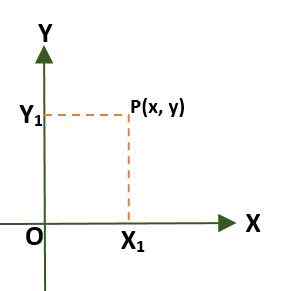
• Sistem Koordinat Kutub (dua -dimensi). Dalam hal ini, sistem ini terdiri dari titik O (asal) yang disebut kutub dan semi -river dengan asal atau disebut sumbu kutub. Dalam hal ini, titik p bidang, dengan mengacu pada kutub dan sumbu kutub, diberikan oleh sudut (ɵ), yang dibentuk oleh jarak antara asal dan titik p.

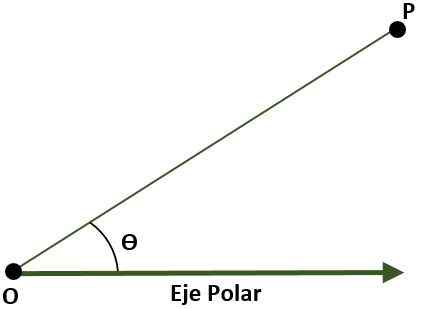
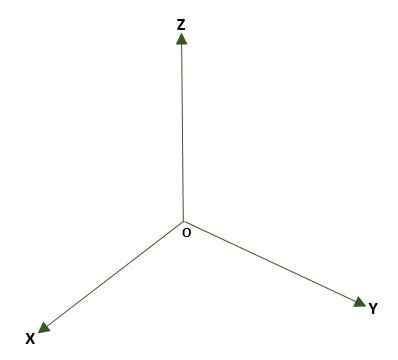
• Sistem tiga dimensi persegi panjang, dibentuk oleh tiga garis tegak lurus (x, y, z) yang memiliki titik atau di luar angkasa. Tiga bidang koordinat dibentuk: xy, xz dan yz; Ruang akan dibagi menjadi delapan daerah yang disebut oktan. Referensi titik p ruang diberikan oleh jarak yang ada antara bidang dan p.

Besaran

Besarnya adalah jumlah fisik yang dapat dihitung atau diukur melalui nilai numerik, seperti dalam kasus beberapa fenomena fisik; Namun, sering kali perlu menggambarkan fenomena ini dengan faktor -faktor lain yang tidak numerik. Itulah sebabnya magnitudo diklasifikasikan menjadi dua jenis:

Besarnya skalar

Mereka adalah jumlah yang didefinisikan dan diwakili secara numerik; yaitu dengan modul bersama dengan satuan ukuran. Misalnya:

a) Waktu: 5 detik.

b) Massa: 10 kg.

c) Volume: 40 ml.

D) Suhu: 40 ºC.

Besarnya vektor

Mereka adalah jumlah yang didefinisikan dan diwakili oleh modul bersama dengan unit, serta oleh indera dan arah. Misalnya:

Dapat melayani Anda: simbolisasi ekspresi

A) Kecepatan: (5ȋ - 3ĵ) m/s.

b) Akselerasi: 13 m /s²; S 45º e.

c) kekuatan: 280 N, 120º.

D) Berat: -40 ĵ kg -f.

Magnitudo vektor secara grafis diwakili oleh vektor.

Apa itu vektor?

Vektor adalah representasi grafis dari besarnya vektor; yaitu, mereka adalah segmen garis di mana ujung terakhirnya adalah ujung panah.

Ini ditentukan oleh modul atau panjang segmennya, indera mereka yang ditunjukkan oleh ujung panahnya dan arahnya sesuai dengan garis tempat ia berada. Asal usul vektor juga dikenal sebagai titik aplikasi.

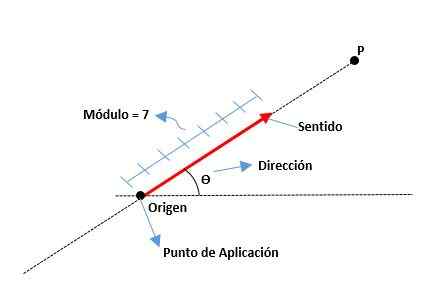
Elemen vektor adalah sebagai berikut:

Modul

Itu adalah jarak dari asal ke akhir vektor, diwakili oleh bilangan real bersama dengan unit. Misalnya:

| Om | = | A | = A = 6 cm

Alamat

Ini adalah ukuran sudut yang ada antara sumbu x (dari positif) dan vektor, serta titik -titik utama (utara, selatan, timur dan barat) juga digunakan.

Nalar

Itu diberikan oleh ujung panah yang terletak di ujung vektor, menunjukkan di mana ini diarahkan.

Klasifikasi vektor

Secara umum, vektor diklasifikasikan sebagai:

Vektor tetap

Itu adalah orang yang titik aplikasinya diperbaiki; Artinya, tetap terkait dengan ruang ruang, jadi tidak bisa bergerak dalam hal ini.

Vektor gratis

Itu dapat bergerak bebas di ruang angkasa karena asalnya bergerak ke titik mana pun tanpa mengubah modul, makna atau arahnya.

Vektor geser

Itu adalah salah satu yang dapat mentransfer asalnya di sepanjang garis tindakannya tanpa mengubah modul, makna atau arahnya.

Properti Vektor

Di antara sifat utama vektor adalah sebagai berikut:

Vektor peralatan

Mereka adalah vektor bebas yang memiliki modul yang sama, arah (atau ini paralel) dan indera sebagai vektor geser atau vektor tetap.

Vektor yang setara

Itu terjadi ketika dua vektor memiliki alamat yang sama (atau paralel), pengertian yang sama, dan meskipun memiliki modul dan titik aplikasi yang berbeda, mereka menyebabkan efek yang sama.

Kesetaraan vektor

Ini memiliki modul, arah, dan indera yang sama, bahkan ketika titik awalnya berbeda, yang memungkinkan vektor paralel untuk pindah ke dirinya sendiri tanpa memengaruhinya.

Vektor yang berlawanan

Mereka adalah mereka yang memiliki modul dan arah yang sama, tetapi maknanya berlawanan.

Vektor kesatuan

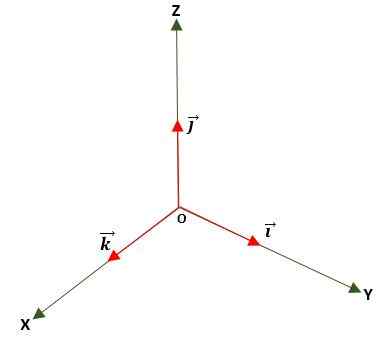
Ini adalah salah satu di mana modul sama dengan unit (1). Ini diperoleh dengan membagi vektor dengan modulnya dan digunakan untuk menentukan arah dan arah vektor, baik di bidang atau di ruang angkasa, menggunakan basis standar atau vektor unit, yaitu:

Vektor nol

Itu adalah orang yang modulnya sama dengan 0; yaitu, titik asalnya dan ekstrem bertepatan pada titik yang sama.

Komponen vektor

Komponen vektor adalah nilai -nilai proyeksi vektor pada sumbu sistem referensi; Tergantung pada dekomposisi vektor, yang dapat dalam sumbu dua atau tiga dimensi, dua atau tiga komponen akan diperoleh, masing -masing.

Komponen vektor adalah bilangan real, yang bisa positif, negatif atau bahkan nol (0).

Dengan cara ini, jika Anda memiliki vektor ā, yang berasal dari sistem koordinat persegi panjang di bidang XY (dua -dimensi), proyeksi pada sumbu x adalah āx dan proyeksi pada sumbu y dan āy. Dengan demikian, vektor akan dinyatakan sebagai jumlah vektor komponennya.

Contoh

Contoh pertama

Anda memiliki vektor ā yang dimulai dari asal dan koordinat ujungnya diberikan. Dengan demikian, vektor ā = (ā_X; KE_Dan) = (4; 5) cm.

Dapat melayani Anda: 120 pembagi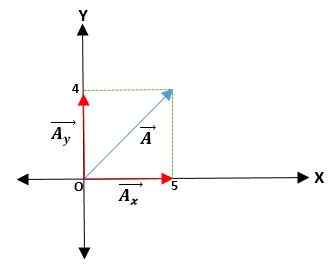

Jika vektor ā bertindak pada asal sistem koordinat segitiga tiga dimensi (di ruang angkasa) x, y, z, ke titik lain (p), proyeksi pada sumbu mereka adalah āx, āy dan āz; Dengan demikian, vektor akan dinyatakan sebagai jumlah dari tiga vektor komponennya.

Contoh kedua

Anda memiliki vektor ā yang dimulai dari asal dan koordinat ujungnya diberikan. Dengan demikian, vektor ā = (a_X; KE_Dan; KE_z) = (4; 6; -3) cm.

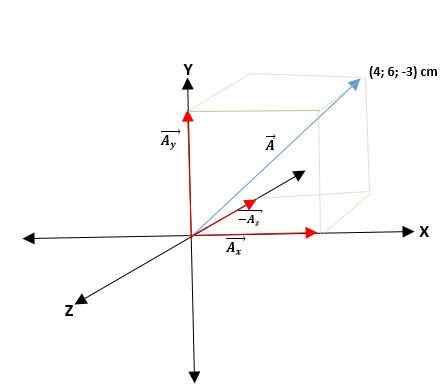
Vektor yang memiliki koordinat persegi panjang dapat diekspresikan sesuai dengan vektor dasar mereka. Untuk itu, hanya setiap koordinat yang harus dikalikan dengan vektor unit masing -masing, sehingga untuk pesawat dan ruang mereka akan menjadi sebagai berikut:

Untuk pesawat: ā = a_Xi +a_DanJ.

Untuk ruang: ā = a_Xi +a_DanJ+a_zk.

Operasi dengan vektor

Ada banyak besaran yang memiliki modul, makna dan arah, seperti akselerasi, kecepatan, perpindahan, kekuatan, antara lain.

Ini diterapkan di berbagai bidang sains, dan untuk menerapkannya, perlu dalam beberapa kasus untuk melakukan operasi seperti jumlah, pengurangan, perkalian dan pembagian vektor dan skalar.

tambahan dan pengurangan vektor

Jumlah dan pengurangan vektor dianggap sebagai operasi aljabar tunggal karena pengurangan dapat ditulis sebagai jumlah; Misalnya, pengurangan vektor ā dan ē dapat dinyatakan sebagai:

Ā - ē = ā + (-ē)

Ada berbagai metode untuk melakukan jumlah dan pengurangan vektor: mereka dapat berupa grafik atau analitik.

Metode grafis

Digunakan saat vektor memiliki modul, indera dan arah. Untuk ini, garis ditarik yang membentuk gambar yang selanjutnya membantu menentukan hasil yang dihasilkan. Di antara yang paling terkenal adalah sebagai berikut:

Metode jajaran genjang

Untuk membuat jumlah atau pengurangan dua vektor, titik umum dipilih pada sumbu koordinat -yang akan mewakili titik asal vektor -, mempertahankan modul, arah, dan arah mereka.

Kemudian garis paralel ditarik ke vektor untuk membentuk jajaran genjang. Vektor yang dihasilkan adalah diagonal yang pergi dari titik asal kedua vektor ke titik jajaran genjang:

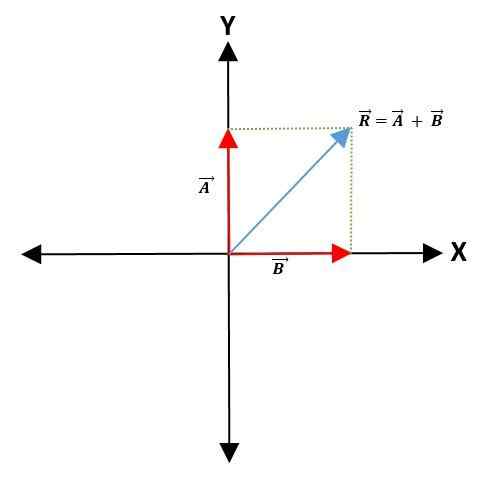
Metode segitiga

Dalam metode ini vektor ditempatkan di bawah yang lain, mempertahankan modul, indera, dan alamatnya. Vektor yang dihasilkan akan menjadi penyatuan asal vektor pertama dengan akhir vektor kedua:

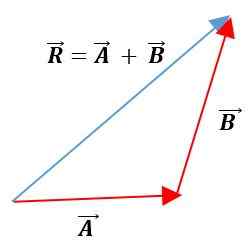
metode analitis

Dua atau lebih vektor dapat ditambahkan atau dikurangi melalui metode geometris atau vektor:

Metode geometris

Saat dua vektor membentuk segitiga atau jajaran genjang, M [odulo dan arah vektor yang dihasilkan dapat ditentukan menggunakan hukum payudara dan kosinus. Dengan demikian, modul vektor yang dihasilkan, menerapkan hukum kosinus dan dengan metode segitiga, diberikan oleh:

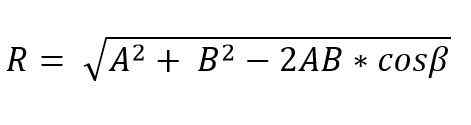
Dalam rumus ini β adalah sudut yang berlawanan dengan sisi R, dan ini sama dengan 180º - ɵ.

Di sisi lain, dengan metode jajaran genjang, modul vektor yang dihasilkan adalah:

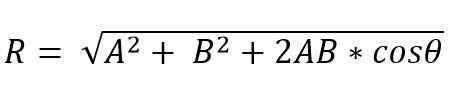
Alamat vektor yang dihasilkan diberikan oleh sudut (α), yang membentuk satu yang dihasilkan dengan salah satu vektor.

Dengan hukum payudara, jumlah atau pengurangan vektor juga dapat dilakukan dengan metode segitiga atau jajaran genjang, mengetahui bahwa di setiap segitiga sisi sebanding dengan payudara sudut yang tampan:

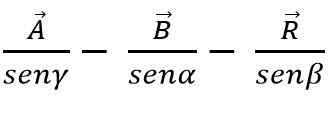
Metode vektor

Ini dapat dilakukan dengan dua cara: tergantung pada koordinat persegi panjang atau vektor dasarnya.

Vektor yang akan ditambahkan atau dikurangi menuju asal koordinat dapat dilakukan, dan kemudian semua proyeksi dipecah menjadi komponen persegi panjang di masing -masing sumbu untuk bidang (x, y) atau ruang (x, x, dan z); Akhirnya, komponennya ditambahkan secara aljabar. Jadi, untuk pesawat itu adalah:

Dapat melayani Anda: bilangan primo: karakteristik, contoh, latihan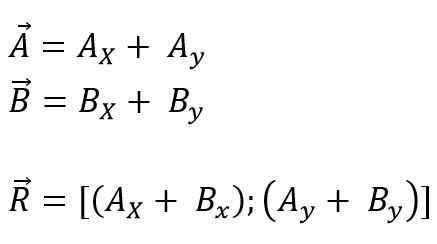

Modul vektor yang dihasilkan adalah:

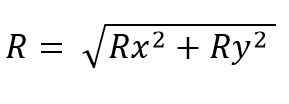
Sedangkan untuk ruang itu:

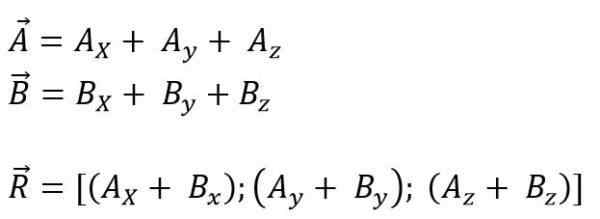
Modul vektor yang dihasilkan adalah:

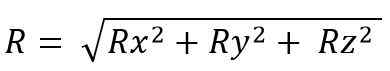
Ketika jumlah vektor dilakukan, beberapa properti diterapkan, yaitu:

• Properti asosiatif: Hasilnya tidak berubah dengan menambahkan dua vektor terlebih dahulu, dan kemudian menambahkan vektor ketiga.
• Properti komutatif: Urutan vektor tidak mengubah hasil yang dihasilkan.
• Properti Distributif Vektor: Jika skalar dikalikan dengan jumlah dua vektor, itu sama dengan penggandaan skalar untuk setiap vektor.
• Scalar properti distributif: Jika vektor dikalikan dengan jumlah dua skalar, itu sama dengan penggandaan vektor untuk setiap skalar.

Perkalian vektor

Penggandaan atau produk vektor dapat dilakukan sebagai jumlah atau pengurangan, tetapi dengan melakukan itu kehilangan makna fisik dan hampir tidak pernah ada dalam aplikasi. Oleh karena itu, umumnya jenis produk yang paling banyak digunakan adalah produk skalar dan vektor.

Produk skalar

Ini juga dikenal sebagai titik dua vektor. Ketika dua modul vektor dikalikan dengan cosinus sudut minor yang terbentuk di antara mereka, skalar diperoleh. Untuk mengekspresikan produk skalar antara dua vektor, titik di antara mereka ditempatkan, dan ini dapat didefinisikan sebagai:

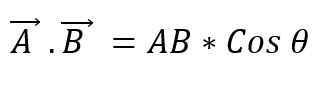
Nilai sudut yang ada antara kedua vektor akan tergantung pada apakah ini paralel atau tegak lurus; Dengan demikian, Anda harus:

• Jika vektor paralel dan memiliki akal sama, coseno 0º = 1.
• Jika vektor paralel dan memiliki indera yang berlawanan, coseno 180º = -1.
• Jika vektor tegak lurus, coseno 90º = 0.

Sudut itu juga dapat dihitung mengetahui hal itu:

Produk skalar memiliki sifat berikut:

• Properti Komutatif: Urutan vektor tidak mengubah skalar.
• Properti Distributif: Jika skalar dikalikan dengan jumlah dua vektor, itu sama dengan penggandaan skalar untuk setiap vektor.

Produk vektor

Perkalian vektor, atau produk silang dari dua vektor A dan B, akan menghasilkan vektor C baru dan mengekspresikan menggunakan salib di antara vektor:

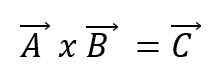
Vektor baru akan memiliki karakteristiknya sendiri. Dengan cara itu:

• Itu alamat: Vektor baru ini akan tegak lurus terhadap pesawat, yang ditentukan oleh vektor asli.
• Dia nalar: Ini ditentukan dengan aturan kanan, di mana vektor A dialihkan ke B yang menunjukkan arah rotasi dengan jari, dan dengan ibu jari arah vektor ditandai.
• Dia modul: Ditentukan oleh multiplikasi modul vektor AXB, oleh dada sudut minor yang ada di antara vektor -vektor ini. Itu diungkapkan:

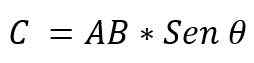
Nilai sudut yang ada antara kedua vektor akan tergantung pada apakah ini paralel atau tegak lurus. Jadi, dimungkinkan untuk menegaskan hal -hal berikut:

• Jika vektor paralel dan memiliki arti yang sama, sinus 0º = 0.
• Jika vektor paralel dan memiliki indera yang berlawanan, sinus 180º = 0.
• Jika vektor tegak lurus, sinus 90º = 1.

Ketika produk vektor diekspresikan sesuai dengan vektor dasarnya, ia harus:

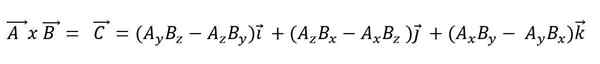
Produk skalar memiliki sifat berikut:

• Itu bukan komutatif: urutan vektor mengubah skalar.
• Properti Distributif: Jika skalar dikalikan dengan jumlah dua vektor, itu sama dengan penggandaan skalar untuk setiap vektor.