Fermat membatasi apa yang terdiri dari dan latihan diselesaikan

Dia Batas fermat Ini adalah metode numerik yang digunakan untuk mencapai nilai kemiringan garis, yang bersinggungan dengan fungsi spesifik dari domainnya. Ini juga digunakan dalam memperoleh titik kritis suatu fungsi. Ekspresinya didefinisikan sebagai:

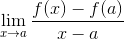
Jelas bahwa Fermat tidak tahu dasar derivasi, namun studinya yang mempromosikan sekelompok ahli matematika untuk menanyakan tentang garis tangen dan aplikasi mereka dalam perhitungan.

[TOC]

Apa batas Fermat?

Ini terdiri dari pendekatan 2 poin, yang dalam kondisi sebelumnya membentuk garis penjelasan ke fungsi dengan persimpangan dalam pasangan nilai.

Saat mendekati variabel ke nilai "A", sepasang poin berkewajiban untuk bertemu. Dengan cara ini garis pengeringan yang sebelumnya menjadi singgung ke titik (a; f (a)).

Nilai hasil bagi (x - a), ketika dievaluasi pada titik "a", melempar ketidakpastian batas tipe k antara nol (k/0). Di mana ketidakpastian ini dapat dipecah melalui teknik faktorisasi yang berbeda.

Teknik operasi yang paling banyak digunakan adalah:

-Perbedaan persegi (a² - B² ) = (a + b) (a - b); Keberadaan elemen (A-B) menyiratkan dalam banyak kasus faktor yang menyederhanakan ekspresi (x-a) dalam rasio batas fermat.

- Penyelesaian persegi (kapak² + bx); Setelah menyelesaikan kotak, Binomial Newton diperoleh, di mana salah satu dari 2 faktornya disederhanakan dengan ekspresi (x - a), memecahkan ketidakpastian.

- Konjugat (a + b) / (a ​​+ b); Lipat gandakan dan bagi ekspresi dengan konjugat beberapa faktor dapat sangat membantu untuk memecahkan ketidakpastian.

- Faktor umum; Dalam banyak kasus hasil pengoperasian pembilang fermat f (x) - f (a) disembunyikan pada faktor (x - a) yang diperlukan untuk membuat faktorisasi. Untuk ini diamati dengan hati -hati elemen apa yang diulangi dalam setiap faktor ekspresi.

Dapat melayani Anda: berapa persepuluh yang ada di satu unit?

Aplikasi Batas Fermat untuk maksimum dan minimum

Bahkan ketika batas Fermat tidak membedakan antara maksimum dan minimum.

Pengetahuan dasar tentang teori grafis fungsi dalam pengabaian dengan teorema ini, dapat cukup untuk menetapkan nilai maksimum dan minimum antara fungsi. Faktanya, titik belok dapat ditentukan oleh teorema nilai rata -rata tambahan untuk teorema Fermat.

Perumpamaan kubik

Paradoks paling signifikan untuk Fermat datang saat mempelajari perumpamaan kubik. Karena perhatiannya ditujukan pada garis singgung suatu fungsi untuk titik tertentu, ia mengalami masalah mendefinisikan garis garis singgung tersebut pada titik infleksi yang ada dalam fungsi tersebut.

Tampaknya mustahil untuk menentukan garis garis singgung ke titik tertentu. Maka dimulailah penyelidikan yang akan menimbulkan kalkulus diferensial. Kemudian ditentukan oleh eksponen penting matematika.

Maximus dan minim

Studi tentang fungsi maksimum dan minimum adalah tantangan untuk matematika klasik, di mana metode yang tegas dan praktis untuk definisi ini.

Fermat membuat metode berdasarkan pengoperasian nilai diferensial kecil, yang setelah proses faktorisasi dihilangkan dengan memberi jalan ke nilai terbanyak dan minimal.

Variabel ini harus dievaluasi dalam ekspresi asli untuk menentukan koordinat titik tersebut, yang bersama -sama dengan kriteria analitik akan ditentukan oleh maksimum atau minimum ekspresi.

metode

Dalam metodenya, Fermat menggunakan simbolisme literal Vieta, yang terdiri dari penggunaan huruf kapital eksklusif: vokal, untuk yang tidak diketahui, dan konsonan untuk jumlah yang diketahui yang diketahui.

Dapat melayani Anda: paralelepiped

Dalam kasus nilai radikal, Fermat menerapkan proses tertentu, yang nantinya akan digunakan dalam faktorisasi batas ketidakpastian Infinity Antara Infinity.

Proses ini terdiri dari membagi setiap ekspresi dengan nilai diferensial yang digunakan. Dalam kasus Fermat menggunakan huruf E, di mana setelah pembagian antara kekuatan terbesar E, nilai yang dicari dari titik kritis menjadi jelas.

Sejarah

Batas Fermat sebenarnya adalah salah satu kontribusi paling terkenal dalam daftar panjang ahli matematika. Studinya berasal dari bilangan prima, pada dasarnya membuat basis untuk perhitungan.

Pada gilirannya, Fermat dikenal karena eksentriknya mengenai hipotesisnya. Itu umum untuk semacam tantangan bagi ahli matematika lain saat itu, ketika dia sudah memiliki solusi atau demonstrasi.

Itu memiliki banyak sekali sengketa dan aliansi dengan ahli matematika yang berbeda pada waktu itu, yang mencintai atau benci bekerja dengannya.

Teorema terakhirnya adalah yang utama yang bertanggung jawab atas ketenaran dunianya, di mana ia mengatakan bahwa generalisasi teorema Pythagoras Untuk gelar "n" apa pun, itu tidak mungkin. Dikatakan memiliki demonstrasi yang valid tentang itu, tetapi meninggal sebelum membuatnya publik.

Demonstrasi ini harus menunggu sekitar 350 tahun. Pada tahun 1995, matematikawan Andrew Wiles dan Richard Taylor, mengakhiri kecemasan yang ditinggalkan oleh Fermat, menunjukkan bahwa ia benar melalui demonstrasi yang valid dari teorema terakhirnya.

Latihan

Latihan 1

Tentukan kemiringan garis garis singgung ke kurva f (x) = x² Pada titik (4, 16)

Mengganti ekspresi batas fermat yang Anda miliki:

Dapat melayani Anda: trinomial persegi yang sempurna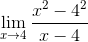

Kemudian menerapkan minimum persegi, pembilang adalah faktor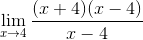

Faktornya disederhanakan (x - 4)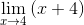

Saat mengevaluasi Anda memilikinya

M = 4 + 4 = 8

Latihan 2

Tentukan titik kritis ekspresi f (x) = x² + 4x menggunakan batas fermat

Dalam hal ini tidak ada koordinat, sehingga nilai x digantikan oleh bentuk generik x₀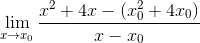

Pengelompokan elemen yang strategis dilakukan, berusaha mengelompokkan rekan X-X₀

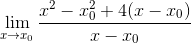
Kotak dikembangkan

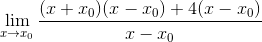
Faktor Umum X-X diamati_{0 dan diekstraksi}

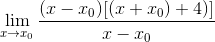
Ekspresi sudah bisa disederhanakan dan ketidakpastian rusak

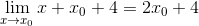
Di titik minimum diketahui bahwa kemiringan garis garis singgung sama dengan nol. Dengan cara ini kita dapat mencocokkan nol ekspresi yang ditemukan dan menghapus nilai x₀    

2 x₀ + 4 = 0

X₀ = -4/2 = -2

Untuk mendapatkan koordinat yang hilang, Anda hanya perlu mengevaluasi poin dalam fungsi asli

F (-2) = (-2)² + 4 (-2) = 4 - 8 = - 4

Titik kritisnya adalah P (-2, -4).

Referensi

1. Analisis nyata. Pendekatan Sejarah Sauhl Stahl, John Wiley & Sons, 5 Agustus. 1999.
2. Karier Matematika Pierre oleh Fermat, 1601-1665: Edisi Kedua. Michael Sean Mahoney. Princeton University Press, 5 Juni. 2018
3. Dari Fermat ke Minkowski: Ceramah tentang Teori Angka dan Pengembangan Sejarahnya. W. Scharlau, h. Opolka, Springer Science & Business Media, 1985
4. Teorema terakhir Fermat: Pengantar Genetik untuk Teori Angka Aljabar. Harold M. Edwards. Springer Science & Business Media, 14 Januari. 2000
5. Fermat Days 85: Matematika untuk Optimalisasi. J.-B. Hiriart-Muruty Elsevier, 1 Jan. 1986